链表反转类算法题

反转链表类

NO1. 反转链表

给定一个长度为 n 的链表，反转该链表，输出表头。

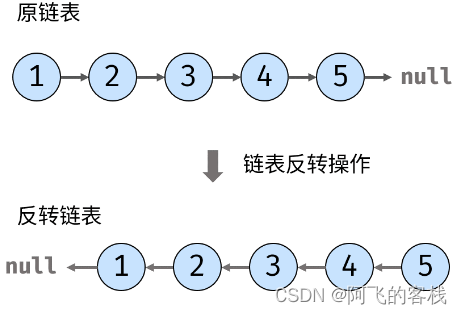
方法一：迭代法（推荐使用）

算法流程：

• step 1 ：特殊情况判断，空链表或只有一个结点的链表，直接返回头结点；
• step 2 ：设置两个指针cur和prev，cur指向当前结点，prev指向上一个结点（初始为 null）；
• step 3 ：遍历整个链表，每到一个结点，断开当前结点cur与下一个结点 cur.next 的指针，并用临时变量 temp 记录下一个结点，然后当前结点的next指向上一个结点（实现反转）；
  • 轮换cur与上一个结点prev，进行下一个结点反转；
  • 循环退出条件为 cur == null；
• step 4 ：返回 prev（反转后，原尾节点变成头结点）；

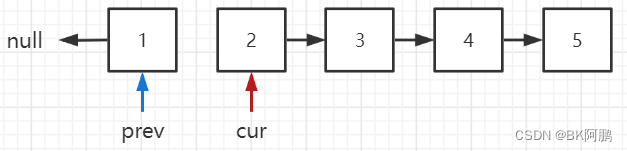
代码实现：

public class Main {
    public ListNode ReverseList(ListNode head) {
        // 特殊情况判断
        if(head == null || head.next == null) 	return head;
        // 双指针
        ListNode prev = null, cur = head;
        while(cur != null) {
            ListNode temp = cur.next;	// 断开链表，要记录后续⼀个
            cur.next = prev;	// 当前的next指针指向前⼀个
            prev = cur;		// 前⼀个更新为当前
            cur = temp;		// 当前更新为刚刚记录的后⼀个
        }
    }
}

复杂度分析：

• 时间复杂度：\(O(N)\)，遍历链表一次；
• 空间复杂度：\(O(1)\)，申请常数个变量；

---

方法二：递归

根据迭代法，每当我们反转链表中某个结点以后，要遍历进入下一个结点进行反转，相当于对后面的子链表进行反转，那这就是一个子问题，因此我们可以使用递归来解决。

• 终止条件：当到达链表尾部，要么当前指针为空，要么下一个指针为空，直接向上层返回当前结点；
• 返回值：每一层向上一层返回翻转后子问题的头结点；
• 本层任务：先进入后一个结点作为子问题，继续反转，然后记录返回的头结点，连接在本层结点的后面；

算法流程：

• step 1 ：递归向下遍历链表，直到遍历到最后一个结点；
• step 2 ：往上一次逆转两个结点；
• step 3 ：逆转后的尾连接本层的结点 head，并断开两节点的原指针（置为 null）；

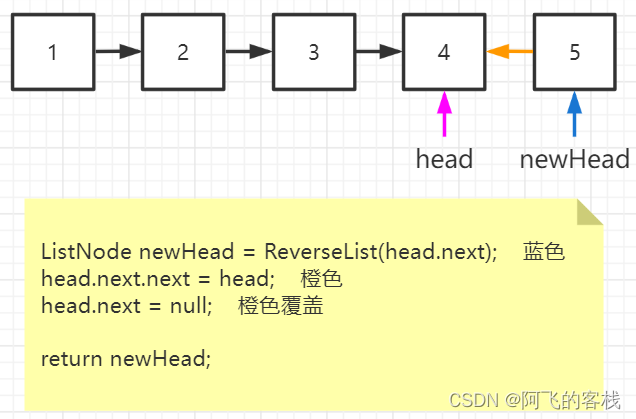
public class Main {
    public ListNode ReverseList(ListNode head) {
        // 递归停止条件
	if(head == null || head.next == null) 	return head;
        ListNode newHead = ReverseList(head.next);	// 反转下一个
        // 本层任务，如
        head.next.next = head;
        head.next = null;
        return newHead;
    }
}

复杂度分析：

• 时间复杂度：\(O(N)\)，遍历链表一次；
• 空间复杂度：\(O(N)\)，递归栈的深度就是链表的长度\(N\)；

NO2. 链表内指定区间反转

将一个结点为 size 的链表 m 位置到 n 位置之间的区间反转；

链表其他部分不变，返回头结点；

方法一：头插法迭代（推荐）

第一步肯定是要先找到第 m 个位置，然后不断反转，直到到达 n 位置；由于m可能为1，即头结点，那反转之后 head 就不再指向头结点了，所以，先构造一个虚拟头结点；

算法流程：

• step 1 ：可以在链表头添加一个虚拟头结点，后续返回时去掉就好了；
• step 2 ：使用两个指针，cur指向当前结点，prev指向前驱节点；
• step 3 ：依次遍历链表，到达第 m 个位置；
• step 4 ：从 m 到 n 位置的结点，依次断掉指向下一个结点的指针，指向前驱，实现反转；
• step 5 ：返回虚拟头结点的next；

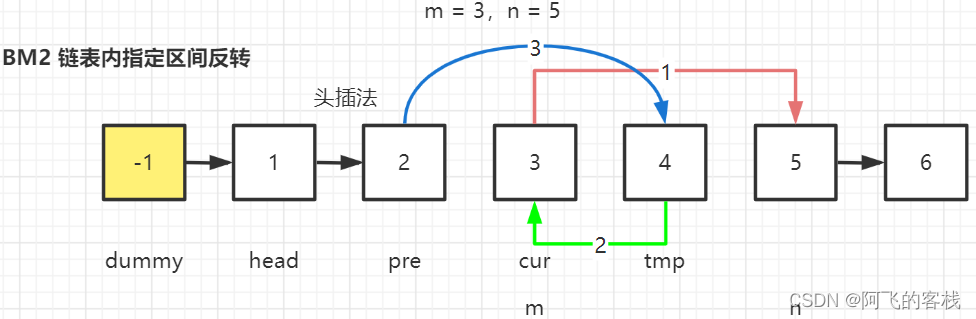
代码实现：

public class Solution {
    public ListNode reverseBetween (ListNode head, int m, int n) {
        // 虚拟头结点
        ListNode dummy = new ListNode(-1);
        dummy.next = head;
        // 双指针（反转链表常规操作）
        ListNode prev = dummy, cur = head;
        // 找到第 m 个结点
        for(int i = 1; i < m; i++) {
            prev = cur;
            cur = cur.next;
        }
        // cur 指向 m，开始反转
        for(int i = m; i < n; i++) {
            ListNode tmp = cur.next;
            cur.next = tmp.next;	// 1
            tmp.next = pre.next;	// 2 开始头插到 pre 后面
            pre.next = tmp;			// 3
        }
        return dummy.next;
    }
}

复杂度分析：

• 时间复杂度：\(O(N)\)，最坏情况下，需要遍历链表一次；
• 空间复杂度：\(O(1)\)，申请常数个变量；

---

方法二：递归

算法流程：

• step 1 ：先利用递归找到反转区间的起点；
• step 2 ：再利用递归从第 n 个位置开始反转，往上拼接；

代码实现：

public class Solution {    
	public ListNode reverseBetween (ListNode head, int m, int n) {
        // 找到第 m 个结点，执行反转
        if(m == 1)    return reverse(head, n);
        // 找 第 m 个结点
        ListNode node = reverseBetween(head.next, m - 1, n - 1);
        head.next = node;	// 拼接已翻转
        return head;
    }
    
    ListNode tmp = null;    // tmp用来暂存第n个结点的后继
    public ListNode reverse(ListNode head, int n){
        // 递归停止
        if(n == 1) {
            tmp = head.next;
            return head;
        }
        ListNode node = reverse(head.next, n - 1);    //进⼊⼦问题
        head.next.next = head; //反转
        head.next = tmp; //拼接
        return node;	// 返回上一层
    }
}

复杂度分析：

• 时间复杂度：\(O(N)\)，最坏情况下，需要遍历链表一次；
• 空间复杂度：\(O(N)\)，最坏情况下，递归栈的深度就是链表的长度\(N\)；

NO.3 链表结点每K个一组翻转

给定一个链表，从头开始每 K 个作为一组，将每组的链表结点翻转；

组与组之间的位置关系保持不变；

如果最后链表末尾剩余不足 K 个结点，则不反转，直接放在尾部；

方法一：头插法迭代

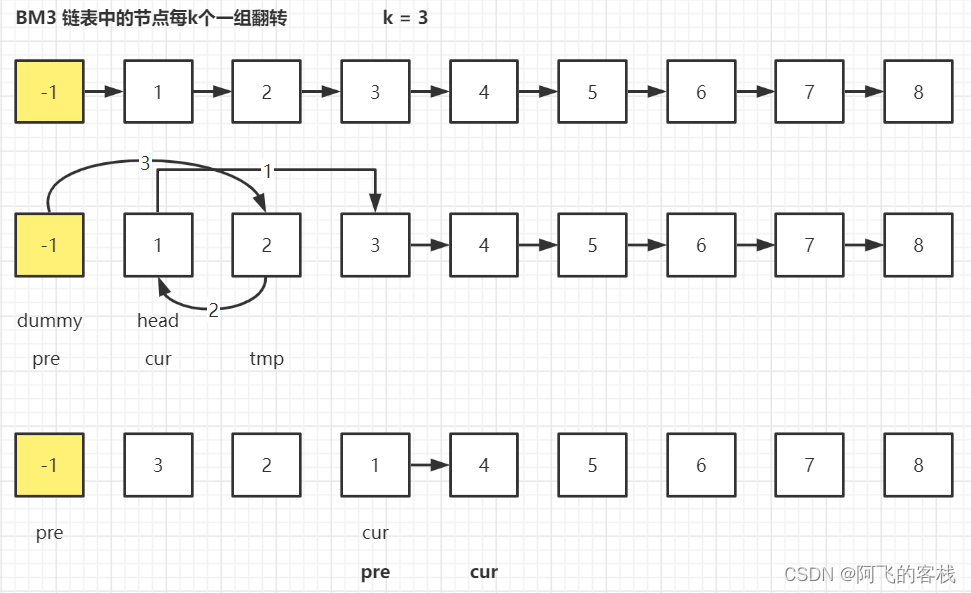
算法流程：

• step 1 ：反转过程中要改变 head 指针，就得设个虚拟头结点，定义双指针 pre和 cur；
• step 2 ：统计链表总长度 len ，用于得出翻转组数 len / k；
• step 3 ：外循环控制翻转组数，内循环控制组内的k个结点翻转（头插 k - 1次）

代码实现：

public class Main {
    public ListNode reverseKGroup (ListNode head, int k) {
        // 特判
        if(head == null || head.next == null || k < 2)	return head;
        // 要改变头结点的，就得设个虚拟头结点
        ListNode dummy = new ListNode(-1);
        dummy.next = head;
        // 双指针，基本操作
        ListNode pre = dummy, cur = head;
        // 统计链表总长度
        int len = 0;
        ListNode p = head;
        while(p != null) {
            len++;
            p = p.next;
        }
        // 翻转组数，仅翻转 len / k
        for(int i = 0; i < len / k; i++) {
            // 外循环控制组数，内循环控制组内的k个结点翻转（头插 k - 1次）
            for(int j = 1; j < k; j++) {
                // 把一组内的结点 temp 头插到 pre 后
                ListNode temp = cur.next;
                cur.next = temp.next;
                temp.next = cur;
                pre.next = temp;
            }
            // 一组翻转完成，去下一组，
            pre = cur;		// pre 指向上一组尾结点 cur
            cur = cur.next;		// cur 指向下一组的第一个结点
        }
        return dummy.next;
    }
}

复杂度分析：

• 时间复杂度：\(O(N)\)，需要遍历链表两次；
• 空间复杂度：\(O(1)\)，申请常数个变量；

---

方法二：递归

终止条件：当进行到最后一个分组，元素个数不足 k 个，就将剩余的最后一个分组直接返回给上层；

返回值：每一层要返回给上层的是翻转后这个分组的头结点，并且后面已经连接好了所有的已翻转好的分组链表；

本层任务：先遍历 k 次，找到该分组尾结点的位置，然后从分组的头结点遍历到尾结点，依次翻转；

算法流程：

• step 1 ：翻转前，找到每次分组的尾节点的下一个结点，即下一分组的头结点
• step 2 ：采用常规的翻转链表操作；
• step 3 ：递归进行拼接；

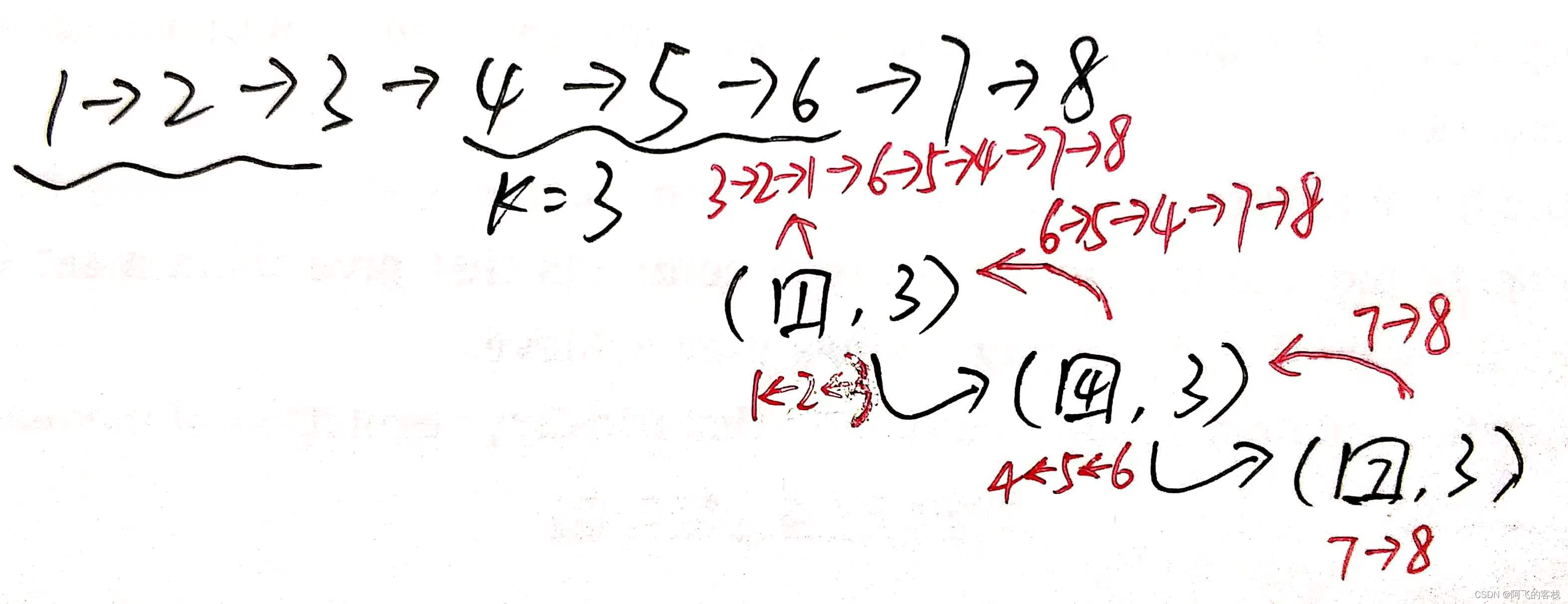
代码实现：

public class Main{
    public ListNode reverseKGroup (ListNode head, int k) {
        
        ListNode tail = head;
        // tail指向本组尾节点的下一个节点，即下一分组的头结点
        for(int i = 0; i < k; i++) {
            // 最后一分组不足 k 个结点，直接向上层返回 head
            if(tail == null)	return head;
            tail = tail.next;
        }
        // 常规的翻转链表操作
        ListNode pre = null, cur = head;
        while(cur != tail) {
            ListNode temp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = temp;
        }
        // 当前尾指向下⼀段要翻转的链表
        head.next = reverseKGroup(tail, k);
        // 
        return pre;
    }
}

复杂度分析：

• 时间复杂度：\(O(N)\)，一共遍历链表 n 个结点；
• 空间复杂度：\(O(1)\)，申请常数个变量；

总结

链表反转类算法题，有两种解决思路：

1. 遍历链表，利用两个滚动指针，不断改变当前结点的 next 指针的指向（当前结点的 next 指向前驱），每次改变指针时都要暂存下一个节点；
2. 头插法，每次把结点头插到 prev 指针后，实现反转；