背包问题（上）
背包问题笔记
2. 01背包问题
有 \(N\) 件物品和一个容量是 \(V\) 的背包。每件物品只能使用一次。
第 \(i\) 件物品的体积是 \(v_i\)，价值是 \(w_i\)。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。
输入：
4 5 （第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积）
1 2 （接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值）
2 4
3 4
4 5
输出：
8
0-1背包问题中要求，每件物品只能选择一次，「0-1 背包」即是不断对第 ii 个物品的做出决策，「0-1」正好代表不选与选两种决定。
| 编号-体积 \ 背包容量 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ① - 1 | 0 | 2 | 2 | 2 | 2 | 2 |
| ② - 2 | 0 | 2 | 4 | 6 | 6 | 6 |
| ③ - 3 | 0 | 2 | 4 | 6 | 6 | 8 |
| ④ - 4 | 0 | 2 | 4 | 6 | 6 | 8 |
方法一：二维dp
动态规划五部曲：
（1）状态定义：dp[i][j]表示第1 ~ i件物品，背包容量为j时能获得的最大价值。
（2）状态初始化：背包容量 j = 0 时，能获得的最大价值为0，即 dp[i][0] 全等于0；
（3）状态转移：
- 当前背包容量放不下第 i 件物品，即
j < v[i]，没得选，前 i 件物品的最大价值就是前 i - 1 件物品的最大价值，转移方程为dp[i][j] = dp[i - 1][j]； - 当前背包容量放得下第 i 件物品，即
j >= v[i]，可选也可不选：- 选择第 i 件物品，则前 i 件物品的最大价值就是前 i - 1 件物品的最大价值（背包剩余空间能刚好放得下第 i 件物品）加上第 i 件物品的价值，转移方程为
dp[i][j] = dp[i - 1][j - v[i]] + w[i]; - 不选第 i 件物品，前 i 件物品的最大价值就是前 i - 1 件物品的最大价值，转移方程为
dp[i][j] = dp[i - 1][j]； - 目的是要得到最大价值，取选和不选两者的最大值：
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])；
- 选择第 i 件物品，则前 i 件物品的最大价值就是前 i - 1 件物品的最大价值（背包剩余空间能刚好放得下第 i 件物品）加上第 i 件物品的价值，转移方程为
（4）遍历方向：
- 由转移方程可知，当前值
dp[i][j]依赖于dp[i - 1][j]或dp[i - 1][j - v[i]]，所以遍历顺序为物品从 1 ~ N，容量从 1 ~ V；
（5）返回值：
- 我们的目标是从N件物品中选择若干件，放入容量为V的背包中，故最大价值为
dp[N][V]；
代码如下：
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt(); // 物品数量
int V = sc.nextInt(); // 背包容积
int[] v = new int[N + 1]; // 第 i 件物品的体积
int[] w = new int[N + 1]; // 第 i 件物品的价值
for(int i = 1; i <= N; i++) {
v[i] = sc.nextInt();
w[i] = sc.nextInt();
}
sc.close();
getMaxVal(N, V, v, w);
}
public static void getMaxVal(int N, int V, int[] v, int[] w) {
// 状态定义：dp[i][j] 对于前i个物品，当前背包容量为j时可以装的最大价值
int[][] dp = new int[N + 1][V + 1];
// base case：dp[0][...] = dp[...][0] = 0 不装物品或背包空间为0时最大价值为0
for(int i = 1; i <= N; i++) { // 遍历物品1~N
for(int j = 1; j <= V; j++) { // 遍历容量1~V
// 当前背包容量j 小于 第i件物品的体积，不把第i个物品入背包
if(j < v[i]) {
dp[i][j] = dp[i - 1][j];
} else {
// 可以把第i个物品装入背包，看不装入和装入时，最大价值哪个大就取哪个
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
}
}
}
System.out.println(dp[N][V]);
// System.out.println(Arrays.deepToString(dp));
}
}
时间复杂度：\(O(N*V)\)；
空间复杂度：\(O(N*V)\)；
方法二：一维dp优化
从方法一中转移方程可以看出，我们定义的状态dp[i][j]可以求得任意合法的i与j的最优解，但题目只需要求得最终状态dp[N][V]，且第 i 件物品的某个状态依赖的是第 i - 1 件物品的某个状态，根本没必要保留之前的dp[i-2][..]等状态值；所以可以省略二维dp中的第一维，采用滚动数组来降低维度，空间从\(O(N*V)\)缩小到\(O(V)\)。
动态规划五部曲：
（1）状态定义：dp[j]表示第1 ~ i件物品（ i 在外循环控制），背包容量为j时能获得的最大价值；
（2）状态初始化：dp[0] = 0，表示背包容量为 j 时，最大价值为 0；
（3）遍历方向：在枚举背包容量 j 时必须得从 V 开始，降序遍历，否则如果是升序，在更新dp[j]时需要用到的前面的状态dp[j - v[i]]已经被污染，但降序不会有这样的问题。
（4）状态转移：
-
转移方程为
dp[j] = max(dp[j], dp[j - v[i]] + w[i])； -
观察上面二维的dp方程，可以优化为以下形式：
for(int i = 1; i <= N; i++) { // 遍历物品1~N for(int j = V; j >= v[i]; j++) { // 遍历容量1~V // 当前背包容量j 小于 第i件物品的体积，不把第i个物品入背包 if(j < v[i]) { dp[i][j] = dp[i - 1][j]; // dp[j] = dp[j] } else { // 可以把第i个物品装入背包，看不装入和装入时，最大价值哪个大就取哪个 dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]); // dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]) } } }
（5）返回值：
dp[j]就是前i轮已经决策的物品且背包容量 j 下的最大价值。因此当执行完循环结构后，由于已经决策了所有物品，dp[j]就是N件物品，背包容量为 j 下的最大价值。即一维dp[j]等价于二维dp[N][j]。
再拿例子解释对于某件物品，为何
dp[j]要逆序更新？我们只有上一层dp值的一维数组，更新dp值只能原地滚动更改，注意到，当我们更新索引值较大的dp值时，需要用到索引值较小的上一层dp值
dp[j - v[i]]；也就是说，在更新索引值较大的dp值之前，索引值较小的上一层dp值必须还在，得是i-1层的，还没被更新，所以只能索引从大到小更新。输入： 4 5 （第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积） 1 2 （接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值） 2 4 3 4 4 5 输出： 8
完整代码：
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt(); // 物品数量
int V = sc.nextInt(); // 背包容积
int[] v = new int[N + 1]; // 第 i 件物品的体积
int[] w = new int[N + 1]; // 第 i 件物品的价值
for(int i = 1; i <= N; i++) {
v[i] = sc.nextInt();
w[i] = sc.nextInt();
}
sc.close();
helper(N, V, v, w);
}
public static void helper(int N, int V, int[] v, int[] w) {
int[] dp = new int[V + 1]; // dp[j] 表示N件物品，背包容量为j下的最大价值
for(int i = 1; i <= N; i++) { // 遍历物品 1 ~ N
for(int j = V; j >= v[i]; j--) { // 反向遍历，背包容量
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
System.out.println(dp[V]);
// System.out.println(Arrays.toString(dp));
}
}
时间复杂度：\(O(N*V)\)；
空间复杂度：\(O(1)\)；
3. 完全背包问题
跟0-1背包相比的唯一不同之处在于每种物品都可用无限次，也是求将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大，并输出最大价值。
输入：
4 5 （第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积）
1 2 （接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值）
2 4
3 4
4 5
输出：
10
沿用0-1背包的思路，就是用个三重循环，外循环枚举的是第 i 件物品；中循环枚举的是背包容量 j，j从1~V；内循环枚举物品i的选择个数；
方法一：二维dp
（1）状态定义：dp[i][j]表示第1 ~ i件物品，背包容量为j时能获得的最大价值。
（2）状态初始化：背包容量 j = 0 时，能获得的最大价值为0，即 dp[i][0] 全等于0；
（3）状态转移：
三重循环的二维dp代码：
public static void helper(int N, int V, int[] v, int[] w) {
// dp[i][j] ：前i件物品，放入容量为 j 的背包的最大价值
int[][] dp = new int[N + 1][V + 1];
for(int i = 1; i <= N; i++) { // 第i件物品
for(int j = 1; j <= V; j++) { // 枚举容量，1 ~ V
for(int k = 0; k * v[i] <= j; k++) { // 枚举第i件物品的数量
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
System.out.println(dp[N][V]);
}
观察上面的dp方程，可以发现：
// max的第一个参数就是上一轮求得的 dp[i-1][j]
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - k * v[i]] + k * w[i]);
∴ dp[i][j] = max( dp[i-1, j], dp[i-1, j-v]+w, dp[i-1, j-2*v]+2*w, dp[i-1, j-3*v]+3*w , .....) ①
第二维度j-v，可得：
dp[i][j-v] = max( dp[i-1, j-v], dp[i-1, j-2*v]+w, dp[i-1, j-3*v]+2*w, ....) ②
通过①和②，可得：
dp[i][j] = max(dp[i - 1][j], dp[i][j - v] + w)
这样，内循环k就可以去掉了，优化后完整代码如下：
public static void helper(int N, int V, int[] v, int[] w) {
// dp[i][j] ：前i件物品，放入容量为 j 的背包的最大价值
int[][] dp = new int[N + 1][V + 1];
for(int i = 1; i <= N; i++) { // 第i件物品
for(int j = 1; j <= V; j++) { // 枚举容量，1 ~ V
if(j < v[i]){
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
}
}
}
System.out.println(dp[N][V]);
}
}
方法二：一维dp优化
二维dp中，用了三重循环，最内层循环枚举当前第i件物品的选择次数k，转移方程为 dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - v[i]] + w[i])。根据0-1背包，第 i 件物品的最大价值依赖于第 i - 1 件，所以可以将第一维去掉，采用滚动数组来优化空间。
模拟过程：
首先dp数组初始化全为0：给定物品种类有4种，包最大体积为5，数据来源于题目的输入
dp[j] = max(dp[j], dp[j - v[i]] + w[i])
v[1] = 1, w[1] = 2
v[2] = 2, w[2] = 4
v[3] = 3, w[3] = 4
v[4] = 4, w[4] = 5
i = 1 时： j从v[1]到5
dp[1] = max(dp[1],dp[0]+w[1]) = w[1] = 2 (用了一件物品1）
dp[2] = max(dp[2],dp[1]+w[1]) = w[1] + w[1] = 4（用了两件物品1）
dp[3] = max(dp[3],dp[2]+w[1]) = w[1] + w[1] + w[1] = 6（用了三件物品1）
dp[4] = max(dp[4],dp[3]+w[1]) = w[1] + w[1] + w[1] + w[1] = 8（用了四件物品1）
dp[5] = max(dp[3],dp[2]+w[1]) = w[1] + w[1] + w[1] + w[1] + w[1] = 10（用了五件物品1）
i = 2 时：j从v[2]到5
dp[2] = max(dp[2],dp[0]+w[2]) = w[1] + w[1] = w[2] = 4（用了两件物品1或者一件物品2）
dp[3] = max(dp[3],dp[1]+w[2]) = 3 * w[1] = w[1] + w[2] = 6（用了三件物品1，或者一件物品1和一件物品2）
dp[4] = max(dp[4],dp[2]+w[2]) = 4 * w[1] = dp[2] + w[2] = 8（用了四件物品1或者，两件物品1和一件物品2或两件物品2）
dp[5] = max(dp[5],dp[3]+w[2]) = 5 * w[1] = dp[3] + w[2] = 10（用了五件物品1或，三件物品1和一件物品2或一件物品1和两件物品2）
i = 3时：j从v[3]到5
dp[3] = max(dp[3],dp[0]+w[3]) = dp[3] = 6 # 保持第二轮的状态
dp[4] = max(dp[4],dp[1]+w[3]) = dp[4] = 8 # 保持第二轮的状态
dp[5] = max(dp[5],dp[2]+w[3]) = dp[4] = 10 # 保持第二轮的状态
i = 4时：j从v[4]到5
dp[4] = max(dp[4],dp[0]+w[4]) = dp[4] = 10 # 保持第三轮的状态
dp[5] = max(dp[5],dp[1]+w[4]) = dp[5] = 10 # 保持第三轮的状态
上面模拟了完全背包的全部过程，也可以看出，最后一轮的dp[m]即为最终的返回结果。
（1）状态定义：dp[j]表示第1 ~ i件物品（ i 在外循环控制），背包容量为j时能获得的最大价值；
（2）状态初始化：dp[0] = 0，表示背包容量为 j 时，最大价值为 0；
（3）遍历方向：
观察0-1背包和完全背包的异同点：
0-1背包：
二维dp：dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
一维dp：dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]); // j 逆序遍历
完全背包：
二维dp：dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
一维dp：
由于 0-1背包在求 dp[j - v[i]] 时依赖的是第 i - 1维的，如果j从前往后遍历会覆盖掉本次的dp[j - v[i]]，所以需要从大到小遍历；
而完全背包中在求 [j - v[i]] 时依赖的是第 i 维的，所以需要从前往后遍历，如果从后往前，那值就是0了。
（4）状态转移：
- 转移方程为：
dp[j] = max(dp[j], dp[j - v[i]] + w[i])；
（5）返回值：
dp[j]就是前 i 轮已经决策的物品且背包容量 j 下的最大价值，返回dp[V]。
public static void helper(int N, int V, int[] v, int[] w) {
// dp[i][j] ：前i件物品，放入容量为 j 的背包的最大价值
int[] dp = new int[V + 1];
for(int i = 1; i <= N; i++) { // 第i件物品
for(int j = v[i]; j <= V; j++) { // 枚举容量，v[i] ~ V 正序遍历
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
System.out.println(dp[V]);
}
时间复杂度：\(O(N*V)\)；
空间复杂度：\(O(1)\)；
LeetCode背包变式
322. 零钱兑换
给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。
你可以认为每种硬币的数量是无限的。
输入：coins = [1, 2, 5], amount = 11 输出：3 解释：11 = 5 + 5 + 1
暴力递归
这题跟组合问题很像，在数组中不断选择一枚硬币，直到所选硬币的总金额等于amount，则找到了一组解。
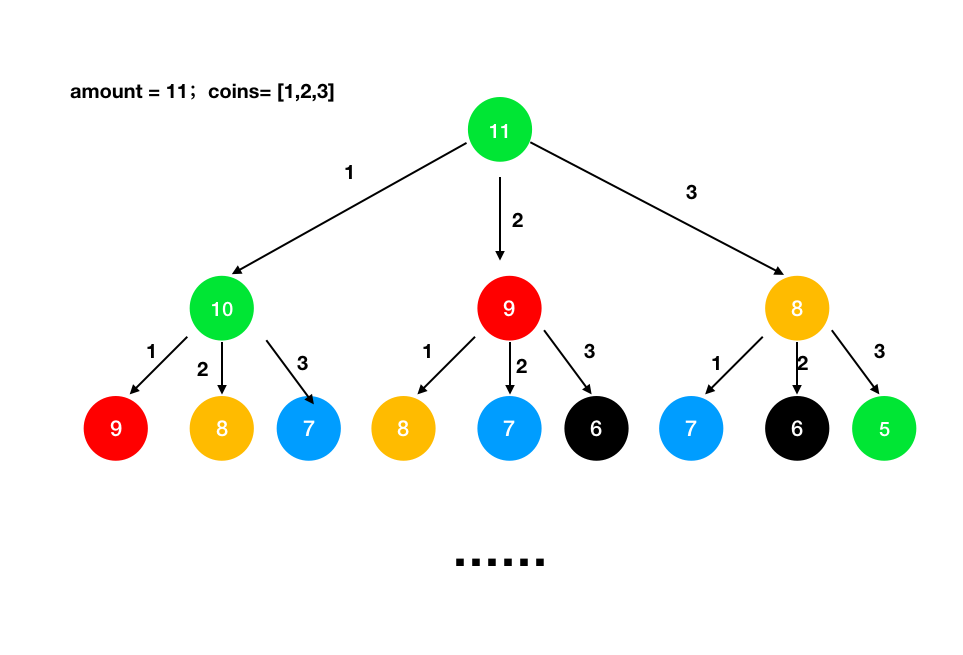
class Solution {
private int res = Integer.MAX_VALUE;
public int coinChange(int[] coins, int amount) {
dfs(coins, amount, 0);
return res == Integer.MAX_VALUE ? -1 : res;
}
// cnt 表示已经找到的凑成方案数
public void dfs(int[] coins, int amount, int cnt) {
// 递归出口
if(amount < 0) return;
if(amount == 0) res = Math.min(res, cnt);
// 遍历多个硬币，一个硬币就是一棵子树
for(int i = 0; i < coins.length; i++) {
dfs(coins, amount - coins[i], cnt + 1);
}
}
}
不过上面的代码存在许多冗余的计算，如上图所示，红色的9要被算两次，橙色的8要被算3次...，这样会浪费很多时间，提交时直接报超时。
备忘录递归
可以使用一个备忘录数组 mem[] 来保存已经算过的各结点的值，之后直接从数组中找就是了。mem[n]表示金币 n 可以被换取的最少的硬币数，不能换取就为 -1，优化后的代码如下：
class Solution {
private int[] memo;
public int coinChange(int[] coins, int amount) {
// memo[n] : 金额为 n 可以被组成的最少硬币数
memo = new int[amount + 1];
return dfs(coins, amount);
}
// dfs：得到金额为amount下所需的最少硬币数
public int dfs(int[] coins, int amount) {
// 加了硬币后，amount变为负值了，超出，返回-1给上层，不要这枚硬币
if(amount < 0) return -1;
if(amount == 0) return 0;
// 这一步，减少了大量运算，不用递归了，提前return
if(memo[amount] != 0) return memo[amount];
// 保存 amount 下所需的最少硬币数
int min = Integer.MAX_VALUE;
// 遍历硬币
for(int i = 0; i < coins.length; i++) {
int res = dfs(coins, amount - coins[i]);
// 返回值大于等于0，说明此枚硬币可选，最少硬币数 + 1
if(res >= 0 && res < min) min = res + 1;
}
// 保存 amount 下所需的最少硬币数
memo[amount] = (min == Integer.MAX_VALUE ? -1 : min);
return memo[amount];
}
}
执行用时：43 ms, 在所有 Java 提交中击败了5.96%的用户
内存消耗：41.5 MB, 在所有 Java 提交中击败了10.26%的用户
通过测试用例：189 / 189
动态规划
带备忘录的递归没报超时，但时间复杂度还是太高，递归是采用自顶向下的方式统计解，可以采用自底向上的动态规划优化。
状态定义：定义dp[i] : 组成金额 i 所需最少的硬币数量。
转移方程：dp[i] = min(dp[i], dp[i - coins[j]] + 1);，求dp[i]，就得知道前一个状态的最小值，前一个状态就是dp[i - cj]，不断递推；
举个例子：
coins = [1, 2, 3], amount = 6
dp[0] = 0;
dp[1] = min(dp[1], dp[1 - c[0]] + 1);
dp[2] = min(dp[2], dp[2 - c[0]] + 1, dp[2 - c[1]] + 1);
...
代码：
class Solution {
public int coinChange(int[] coins, int amount) {
// dp[i] : 组成金额 i 所需最少的硬币数量
int[] dp = new int[amount + 1];
// 初始定义总金额为amount，所需的最少硬币数为 amount + 1；
Arrays.fill(dp, amount + 1);
dp[0] = 0;
// 外循环遍历从1~amount每个金额，内循环遍历每个硬币
for(int i = 1; i <= amount; i++) {
for(int coin : coins) {
// 硬币面额 小于 金额 i 才会进入if，选择 coin硬币
if(coin <= i) dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
return dp[amount] == amount + 1 ? -1 : dp[amount];
}
}
时间：O(m*c)，m是总金额数，c是硬币面额数，对于每个状态，每次需要枚举c个面额来转移状态；
空间：O(m)，dp数组需要申请长度为m的空间。
