二叉树查找

　　对于符号表，要支持高效的插入操作，就需要一种链式结构。但单链表无法使用二分查找，因为二分查找的高效来自于能够快速通过索引取得任何子数组的中间元素，链表只能遍历（详细描述）。为了将二分查找的效率和链表的灵活性结合，需要更复杂的数据结构：二叉查找树。具体来说，就是使用每个结点含有两个链接的二叉查找树来高效地实现符号表。

　　一棵二叉查找树（BST）是一棵二叉树，其中每个结点都含有一个 IComparable 类型的键以及相关联的值，且每个结点的键都大于其左子树的任意结点的键而小于右子树的任意结点的键。

　　

　　

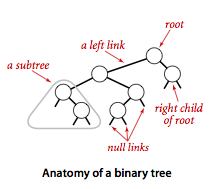
　　1.实现API

　　1.数据结构

public class BinarySearchTreesST<Key, Value> : BaseSymbolTables<Key, Value>
        where Key : IComparable
    {
        private Node root;//二叉树根节点

        /// <summary>
        /// 嵌套定义一个私有类表示二叉查找树上的一个结点。
        /// 每个结点都含有一个键，一个值，一条左连接，一条右连接和一个结点计数器。
        /// 变量 N 给出了以该结点为根的子树的结点总数。
        /// x.N = Size(x.left) + Size(x.right) + 1;
        /// </summary>
        private class Node
        {
            public Key key;
            public Value value;
            public Node left, right;
            public int N;
            public Node(Key key,Value value,int N)
            {
                this.key = key;
                this.value = value;
                this.N = N;
            }
        }

        public override int Size()
        {
            return Size(root);
        }

        private int Size(Node x)
        {
            if (x == null)
                return 0;
            else
                return x.N;
        }
}

　　一棵二叉查找树代表了一组键（及其相应的值）的集合，而一个可以用多棵不同的二叉查找树表（起始根结点不同，树就不同），下面是一种情况。但不管什么情况的树，我们将一棵二叉查找树的所有键投影到一条直线上，一定可以得到一条有序的键列。

　　　　

　　

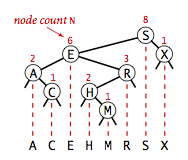
　　2.查找

　　在符号表中查找一个键可能有两种结果：命中和未命中。下面的实现算法是在二叉查找树中查找一个键的递归算法：如果树是空的，则查找未命中，如果被查找的键和根结点的键相等，查找命中，否则就递归地在适当地子树中继续查找。如果被查找的键较小就选择左子树，较大则选择右子树。当找到一个含有被查找键的结点（命中）或者当前子树变为空（未命中）时这个过程才结束。

public override Value Get(Key key)
        {
            return Get(root,key);
        }

        /// <summary>
        /// 
        /// </summary>
        /// <param name="x">第一个参数是结点（子树的根结点）</param>
        /// <param name="key">第二个参数是被查找的键</param>
        /// <returns></returns>
        private Value Get(Node x, Key key)
        {
            if (x == null)
                return default(Value);

            int cmp = key.CompareTo(x.key);
            if (cmp < 0)
                return Get(x.left, key);
            else if (cmp > 0)
                return Get(x.right, key);
            else
                return x.value;
        }

　　

 

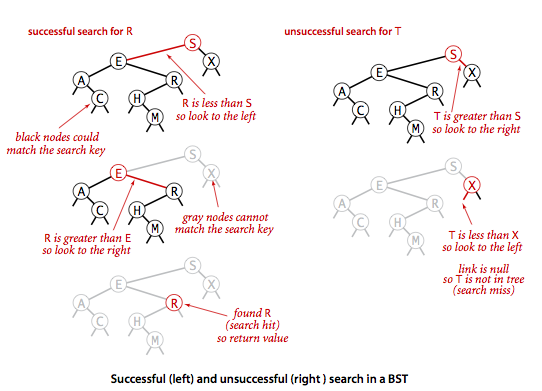
　　3.插入

　　插入方法和查找的实现差不多，当查找一个不存在于树中的结点并结束于一条空连接时，需要将连接指向一个含有被查找的键的新节点。下面插入方法的逻辑：如果树是空的，就返回一个含有该键值对的新结点赋值给这个空连接；如果被查找的键小于根结点的键，继续在左子树中插入该键，否则就在右子树中插入。并且需要更新计数器。

public override void Put(Key key, Value value)
        {
            root = Put(root,key,value);
        }

        private Node Put(Node x, Key key, Value value)
        {
            if (x == null)
                return new Node(key,value,1);
            int cmp = key.CompareTo(x.key);
            if (cmp < 0)
                x.left = Put(x.left, key, value); //注意 x.left = 的意思
            else if (cmp > 0)
                x.right = Put(x.right, key, value);//注意 x.right =
            else
                x.value = value;

            x.N = Size(x.left) + Size(x.right) + 1;
            return x;
        }

　　　　

 

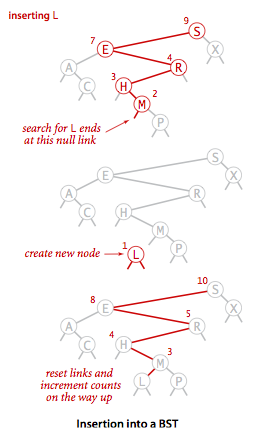
　　在查找和插入的递归实现中，可以将递归调用前的代码想象成沿着树向下走，将递归调用后的代码想象成沿着树向上爬。对于 Get 方法，这对应着一系列的返回指令。对于 Put 方法，意味着重置搜索路径上每个父结点指向子结点的连接，并增加路径上每个结点中计数器的值。在一棵简单的二叉查找树中，唯一的新连接就是在最底层指向新结点的连接，重置更上层的连接可以通过比较语句来避免。

　　

　　4.分析

　　二叉查找树上算法的运行时间取决于树的形状，而树的形状又取决于键的插入顺序。在最好情况下，一棵含有 N 个结点的树是完全平衡的，每条空连接和根结点的距离都是 ~lgN 。在最坏情况下，搜索路径上有 N 个结点。

　　

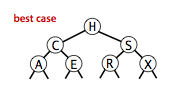
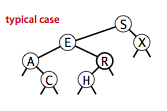
　　对于随机模型的分析而言，二叉查找树和快速排序很相似。根结点就是快速排序中的第一个切分元素，对于其他子树也同样使用。

　　在由 N 个随机键构造的二叉查找树，查找命中的平均所需的比较次数为 ~2lnN （约1.39lgN），插入和查找未命中平均所需的比较次数也为  ~2lnN （约1.39lgN）。插入和查找未命中比查找命中需要一次额外比较。

　　由此可知，在二叉查找树中查找比二分查找的成本高出约 39% ，但是插入操作所需的成本达到了对数界别。

 

　　5.有序性相关的方法和删除操作

　　1.最大键和最小键

　　如果根结点的左连接为空，那么一棵二叉查找树中最小的键就是根结点；如果左连接非空，那么树中的最小键就是左子树中的最小键。

        public override Key Min()
        {
            return Min(root).key;
        }

        private Node Min(Node x)
        {
            if (x.left == null)
                return x;
            return Min(x.left);
        }

 

　　2.向上取整和向下取整

　　如果给定的键 key 小于二叉查找树的根结点的键，那么小于等于 key 的最大键 Floor( key ) 一定在根结点的左子树中；如果给定的键大于二叉查找树的根结点，那么只有当根节点的右子树中存在小于等于给定键的结点时，小于等于给定键的最大键才会出现在右子树中，否则根结点就是小于等于 key 的最大键。

/// <summary>
        /// 向下取整
        /// </summary>
        /// <param name="key"></param>
        /// <returns></returns>
        public override Key Floor(Key key)
        {
            Node x = Floor(root,key);
            if (x == null)
                return default(Key);
            return x.key;
        }

        private Node Floor(Node x, Key key)
        {
            if (x == null)
                return default(Node);
            int cmp = key.CompareTo(x.key);
            if (cmp == 0)
                return x;
            if (cmp < 0)
                return Floor(x.left,key);
            Node t = Floor(x.right,key);
            if (t != null)
                return t;
            else
                return x;
        }

 

　　3.选择操作

　　我们在二叉查找树的每个结点中维护的子树结点计数器变量 N 就是用来支持此操作的。

　　如果要找到排名为 k 的键（即树中正好有 k 个小于它的键）。如果左子树中的结点树 t 大于 k，就继续（递归地）在左子树中查找排名为 k 的键；如果 t == k，就返回根结点的键；如果 t 小于 k，就递归地在右子树中查找排名为 （k-t-1）的键。

public override Key Select(int k)
        {
            return Select(root, k).key;
        }

        private Node Select(Node x, int k)
        {
            if (x == null)
                return default(Node);

            int t = Size(x.left);
            if (t > k)
                return Select(x.left, k);
            else if (t < k)
                return Select(x.right, k - t - 1);
            else
                return x;
        }

 

　　4.排名

　　排名是选择操作的逆方法，它会返回给定键的排名。它的实现和 Select 类似：如果给定的键等于根根结点的键，就返回左子树中的节点数 t ；如果给定的键小于根结点，就返回该键在左子树中的排名（递归计算）；如果给定的键大于根结点，就返回 t+1 (根结点）再加上它在右子树中的排名（递归计算）。

public override int Rank(Key key)
        {
            return Rank(key,root);
        }

        private int Rank(Key key, Node x)
        {
            if (x == null)
                return 0;
            int cmp = key.CompareTo(x.key);
            if (cmp < 0)
                return Rank(key, x.left);
            else if (cmp > 0)
                return 1 + Size(x.left) + Rank(key, x.right);
            else
                return Size(x.left);
        }

 

　　5.删除最大键和删除最小键

　　二叉查找树中最难实现的就是删除操作，我们先实现删除最小键的操作。我们要不断深入根节点的左子树直到遇到一个空连接，然后将指向该结点的连接指向该结点的右子树（只需在 x.left == null 时返回右链接，赋值给上层的左连接）。

/// <summary>
        /// 注意可考虑删除根结点
        /// </summary>
        public override void DeleteMin()
        {
            root = DeleteMin(root);
        }

        private Node DeleteMin(Node x)
        {
            if (x.left == null)
                return x.right;
            x.left = DeleteMin(x.left);
            x.N = Size(x.left) + Size(x.right) + 1;
            return x;
        }

 

　　6.删除操作　　

　　我们 可以使用上面类似的方法删除任意只有一个子结点或者没有子结点的结点，但是无法实现删除有两个子结点的结点的方法。我们在删除 x 结点后用它的右子树最小结点结点填补它的位置，这样就可以保证树的有序性，分四步完成：

　　　　1.将指向即将被删除的结点的连接保存为 t ;

　　　　2.将 x 指向它的后继结点 Min（t.right）；

　　　　3.将 x 的右链接指向 DeleteMin（t.right），也就是删除右子树最小连接，然后返回 t 的右链接；

　　　　4.将 x 的左连接设为 t.left；

        public override void Delete(Key key)
        {
            root = Delete(root,key);
        }

        private Node Delete(Node x, Key key)
        {
            if (x == null)
                return null;
            int cmp = key.CompareTo(x.key);
            if (cmp < 0)
                x.left = Delete(x.left, key);
            else if (cmp > 0)
                x.right = Delete(x.right, key);
            else
            {
                if (x.right == null)
                    return x.left;
                if (x.left == null)
                    return x.right;
                Node t = x;
                x = Min(t.right);
                x.right = DeleteMin(t.right);
                x.left = t.left;
            }
            x.N = Size(x.left) + Size(x.right) + 1;
            return x;
        }

　　该算法有个问题，在选择后继结点应该是随机的，应该考虑树的对成性。

 

　　7.范围查找

　　要实现能够返回给定范围内键的方法 Keys（），需要一个遍历二叉查找树的基本方法，叫做中序遍历。先找出根结点的左子树中的符合的所有键，然后找出根结点的键，最后找出根结点右子树的符合的所有键。

        public override IEnumerable<Key> Keys(Key lo, Key hi)
        {
            Queue<Key> quene = new Queue<Key>();
            Keys(root, quene,lo,hi);
            return quene;
        }

        private void Keys(Node x, Queue<Key> quene, Key lo, Key hi)
        {
            if (x == null)
                return;
            int cmplo = lo.CompareTo(x.key);
            int cmphi = hi.CompareTo(x.key);
            if (cmplo < 0)
                Keys(x.left,quene,lo,hi);
            if (cmplo <= 0 && cmphi >= 0)
                quene.Enqueue(x.key);
            if (cmphi > 0)
                Keys(x.right,quene,lo,hi);
        }

 

　　全部代码

    public class BinarySearchTreesST<Key, Value> : BaseSymbolTables<Key, Value>
        where Key : IComparable
    {
        private Node root;//二叉树根节点

        /// <summary>
        /// 嵌套定义一个私有类表示二叉查找树上的一个结点。
        /// 每个结点都含有一个键，一个值，一条左连接，一条右连接和一个结点计数器。
        /// 变量 N 给出了以该结点为根的子树的结点总数。
        /// x.N = Size(x.left) + Size(x.right) + 1;
        /// </summary>
        private class Node
        {
            public Key key;
            public Value value;
            public Node left, right;
            public int N;
            public Node(Key key,Value value,int N)
            {
                this.key = key;
                this.value = value;
                this.N = N;
            }
        }

        public override int Size()
        {
            return Size(root);
        }

        private int Size(Node x)
        {
            if (x == null)
                return 0;
            else
                return x.N;
        }

        public override Value Get(Key key)
        {
            return Get(root,key);
        }

        /// <summary>
        /// 
        /// </summary>
        /// <param name="x">第一个参数是结点（子树的根结点）</param>
        /// <param name="key">第二个参数是被查找的键</param>
        /// <returns></returns>
        private Value Get(Node x, Key key)
        {
            if (x == null)
                return default(Value);

            int cmp = key.CompareTo(x.key);
            if (cmp < 0)
                return Get(x.left, key);
            else if (cmp > 0)
                return Get(x.right, key);
            else
                return x.value;
        }

        public override void Put(Key key, Value value)
        {
            root = Put(root,key,value);
        }

        private Node Put(Node x, Key key, Value value)
        {
            if (x == null)
                return new Node(key,value,1);
            int cmp = key.CompareTo(x.key);
            if (cmp < 0)
                x.left = Put(x.left, key, value); //注意 x.left = 的意思
            else if (cmp > 0)
                x.right = Put(x.right, key, value);//注意 x.right =
            else
                x.value = value;

            x.N = Size(x.left) + Size(x.right) + 1;
            return x;
        }

        public override Key Min()
        {
            return Min(root).key;
        }

        private Node Min(Node x)
        {
            if (x.left == null)
                return x;
            return Min(x.left);
        }

        /// <summary>
        /// 向下取整
        /// </summary>
        /// <param name="key"></param>
        /// <returns></returns>
        public override Key Floor(Key key)
        {
            Node x = Floor(root,key);
            if (x == null)
                return default(Key);
            return x.key;
        }

        private Node Floor(Node x, Key key)
        {
            if (x == null)
                return default(Node);
            int cmp = key.CompareTo(x.key);
            if (cmp == 0)
                return x;
            if (cmp < 0)
                return Floor(x.left,key);
            Node t = Floor(x.right,key);
            if (t != null)
                return t;
            else
                return x;
        }

        public override Key Select(int k)
        {
            return Select(root, k).key;
        }

        private Node Select(Node x, int k)
        {
            if (x == null)
                return default(Node);

            int t = Size(x.left);
            if (t > k)
                return Select(x.left, k);
            else if (t < k)
                return Select(x.right, k - t - 1);
            else
                return x;
        }

        public override int Rank(Key key)
        {
            return Rank(key,root);
        }

        private int Rank(Key key, Node x)
        {
            if (x == null)
                return 0;
            int cmp = key.CompareTo(x.key);
            if (cmp < 0)
                return Rank(key, x.left);
            else if (cmp > 0)
                return 1 + Size(x.left) + Rank(key, x.right);
            else
                return Size(x.left);
        }

        /// <summary>
        /// 注意可考虑删除根结点
        /// </summary>
        public override void DeleteMin()
        {
            root = DeleteMin(root);
        }

        private Node DeleteMin(Node x)
        {
            if (x.left == null)
                return x.right;
            x.left = DeleteMin(x.left);
            x.N = Size(x.left) + Size(x.right) + 1;
            return x;
        }

        public override void Delete(Key key)
        {
            root = Delete(root,key);
        }

        private Node Delete(Node x, Key key)
        {
            if (x == null)
                return null;
            int cmp = key.CompareTo(x.key);
            if (cmp < 0)
                x.left = Delete(x.left, key);
            else if (cmp > 0)
                x.right = Delete(x.right, key);
            else
            {
                if (x.right == null)
                    return x.left;
                if (x.left == null)
                    return x.right;
                Node t = x;
                x = Min(t.right);
                x.right = DeleteMin(t.right);
                x.left = t.left;
            }
            x.N = Size(x.left) + Size(x.right) + 1;
            return x;
        }

        public override IEnumerable<Key> Keys(Key lo, Key hi)
        {
            Queue<Key> quene = new Queue<Key>();
            Keys(root, quene,lo,hi);
            return quene;
        }

        private void Keys(Node x, Queue<Key> quene, Key lo, Key hi)
        {
            if (x == null)
                return;
            int cmplo = lo.CompareTo(x.key);
            int cmphi = hi.CompareTo(x.key);
            if (cmplo < 0)
                Keys(x.left,quene,lo,hi);
            if (cmplo <= 0 && cmphi >= 0)
                quene.Enqueue(x.key);
            if (cmphi > 0)
                Keys(x.right,quene,lo,hi);
        }
    }

 

　　8.性能分析

　　给定一棵树，树的高度决定了所有操作在最坏情况下的性能（范围查找除外，因为它的额外成本和返回的键的数量成正比），成正比。

　　随机构造的二叉查找树的平均高度为树中结点数量的对数级别，约为 2.99 lgN 。但如果构造树的键不是随机的（例如，顺序或者倒序），性能会大大降低，后面会讲到平衡二叉查找树。

算法	最坏情况下运行时间的增长量级		平均情况下的运行时间的增长量级		是否支持有序性相关操作
	查找	插入	查找命中	插入
顺序查找（无序链表）	N	N	N/2	N	否
二分查找（有序数组）	lgN	N	lgN	N/2	是
二叉树查找	N	N	1.39lgN	1.39lgN	是