快速排序
快速排序是应用最广泛的排序算法，流行的原因是它实现简单，适用于各种不同情况的输入数据且在一般情况下比其他排序都快得多。
快速排序是原地排序（只需要一个很小的辅助栈），将长度为 N 的数组排序所需的时间和 N lg N 成正比。
1.算法
快速排序也是一种分治的排序算法。它将一个数组分成两个子数组，将两部分独立地排序。
快速排序和归并排序是互补：归并排序是将数组分成两个子数组分别排序，并将有序数组归并，这样数组就是有序的了；而快速排序将数组通过切分变成部分有序数组，然后拆成成两个子数组，当两个子数组都有序时整个数组也就有序了。
归并排序的递归调用发生在处理数组之前，快速排序的递归调用是发生在处理数组之后。
快速排序中切分的位置取决于数组的内容。
public class Quick: BaseSort { public new static long usedTimes = 0; public static void Sort(IComparable[] a) { usedTimes = 0; Stopwatch timer = new Stopwatch(); timer.Start(); Sort(a,0,a.Length-1); timer.Stop(); usedTimes = timer.ElapsedMilliseconds; } public static void Sort(IComparable[] a, int lo, int hi) { if (hi <= lo) return; //切分 int j = Partition(a,lo,hi); //Console.WriteLine(j); Sort(a,lo,j-1); Sort(a,j+1,hi); } public static int CompareCount = 0; public static int Partition(IComparable[] a, int lo, int hi) { int i = lo; int j = hi + 1; var v = a[lo]; while (true) { //从左往右依次和 v 比较，直到找到 >= v 的值 索引i （索引i 左边的值都小于切分元素） while (Less(a[++i], v)) { CompareCount++; if (i == hi) break; } //从右往左依次和 v 比较，直到找到 <= v 的值 索引j（索引j 右边的值都大于于切分元素） while (Less(v, a[--j])) { CompareCount++; if (j == lo) break; } //当 i >= j 时就找到了切分元素位置，位置为 j ,退出循环 if (i >= j) break; //如果 i 和 j 没有相遇，将 i 和 j 的值交换，继续循环，直到相遇 Exch(a,i,j); } //将切分元素放到切分位置 j Exch(a,lo,j); return j; } }
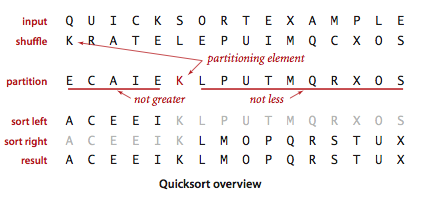
该算法的关键在于切分 ，在 Sort(IComparable[] a, int lo, int hi) 方法中，切分后 a[lo] 到 a[j-1] 中的所有元素都不大于 a[ j ] ，a[j+1] 到 a[ hi ] 中的所有元素都不小于 a[ j ] ，然后对左子数组和右子数组进行递归。因为切分的过程总能排定一个元素，当切分到剩一个元素时，子数组就是有序的。当左数组和右数组都有序时，整个数组也就有序了。
切分方法：先随意取 a[ lo ] 作为切分元素，即那个将被排定的元素。然后从数组的左端向右扫描直到找到大于等于它的元素，再从数组右端向左开始扫描直到找到小于等于它的元素。如果找到的这两个元素不是同一个元素（索引不同），那么这个元素就还没被排定；如果相同意味着这个元素已被排定。如果没被排定，就交换这两个元素，继续扫描，直到左右索引相遇，即可返回将切分元素和找到的索引位置的元素交换，返回索引 j 。
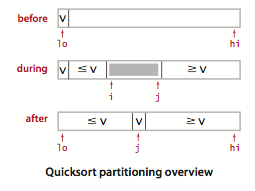
排序实列：
注意点
1. 原地切分
该算法是原地切分，如果使用辅助数组需要将切分后的数组复制回去的额外开销。
2.越界
要防止扫描指针跑出数组边界。
3.保持随机性
该算法对所有子数组都是一视同仁的。
4.终止循环
该算法有三个循环都要注意什么时候终止。
5.处理切分元素值有重复的情况
该算法左右扫描都会在遇到相等值时停下来，尽管这样会不必要的等值交换，但在某些情况下能够避免算法的运行时间变为平方级别。
6.终止递归
任何递归调用都要先考虑什么时候终止。
2.性能
快速排序运行时间的增长量级为 NlogN 。
快速排序切分方法的内循环用一个递增的索引将数组元素和一个定值比较，这种循环很简洁。它比归并排序和希尔排序都快，因为归并排序和希尔排序在内循环中移动元素。
快速排序的另一个速度优势在于它的比较次数很少（如果每次都对半分的话需要 N/2 * logN 次比较）。但是排序效率还是依赖切分数组的效果，而这依赖于切分元素的值 。切分一个较大的数据组，切分可能发生在任何一个位置。
快速排序的最好情况是每次都能将数组对半分。在这种情况下快速排序所用的比较次数正好满足分治递归的 C(N) = 2C(N/2) + N 公式。2C(N/2) 表示将两个子数组排序的成本， N 表示 切分元素和所有数组元素比较的成本。 C(N) ~ N log N 。平均而言切分元素都能落在数组中间。
快速排序在最坏情况下需要 ~ N^2 / 2 次比较，即每次切分总有一个数组是空的（逆序），比较次数为： N + （N-1）+ (N-2) ...+2+1 = (N+1)N/2 。这种情况不仅算法所需的时间是平方级别的，所需的空间是线性的。
快速排序平均需要 ~ 2N lnN 次比较（以及1/6的交换）。归并排序也可以做到这个量级，但是快速排序移动数据次数少（即交换次数），所以快速排序更快，尽管比较次数比归并排序多了约 39%。
当数组切分不平衡时（第一次用最小的切分，第二次用第二小的切分...）会倒置一个大数组需要切分很多次（上面说的逆序），所以非重复数组需要随机打乱；当存在大量重复元素时，排序过程会进行很多次交换，重复数组可以使用稍后提到的三向切分的快速排序。
3.改进
1.切换到插入排序
当将一个大数组切分成一定小的数组时使用插入排序给小数组排序，这样就不需要继续递归调用 Sort() 方法了。
将 if (hi <= lo) return; 改为
if（hi <= lo + M）{ Insertion.Sort(a, lo, hi); return;}
转换参数 M 的最佳值和系统相关，5 ~ 15 最佳。
2.三取样切分
改进快速排序性能的另一个方法是使用子数组的一小部分元素的中位数来切分数组。这样得到的切分更好，但是需要计算中位数。一般取样大小为3并用大小居中的元素切分最好。
3.熵最优排序
实际应用中经常会出现大量重复元素的数组，这会影响快排的性能。例如，一个全部重复的子数组就不需要排序了，但上面的算法会继续切分。三向切分的快速排序可以将有大量重复元素的数组从线性对数级别提高到线性级别。
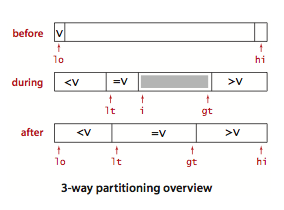
三向切分是将数组切分成小于，等于和大于三部分。它从左到右遍历数组一次，维护一个指针 lt 使得 a[lo ... lt-1] 中的元素都小于 v（切分元素），一个指针 gt 使得 a[gt+1 ... hi] 中的元素都大于 v ，一个指针 i 使得 a[ lt ... i ] 中元素都等于 v , a[ i ... gt ] 中的元素都还未确定。一开始 lo 和 i 相等：
- a[i]小于v：与 a[i] 交换 a[lt] 并增加lt 和i
- a[i]大于v：将 a[i] 与 a[gt] 交换并减少gt
- a[i]等于v：递增i
public class Quick: BaseSort { public new static long usedTimes = 0; //三向切分 public static void Sort3Way(IComparable[] a) { usedTimes = 0; Stopwatch timer = new Stopwatch(); timer.Start(); Sort3Way(a, 0, a.Length - 1); timer.Stop(); usedTimes = timer.ElapsedMilliseconds; } public static void Sort3Way(IComparable[] a, int lo, int hi) { if (hi < lo) return; int lt = lo, i = lo + 1, gt = hi; IComparable v = a[lo]; while (i <= gt) { int cmp = a[i].CompareTo(v); if (cmp < 0) Exch(a, lt++, i++); else if (cmp > 0) Exch(a, i, gt--); else i++; } Sort3Way(a,lo,lt-1); Sort3Way(a,gt+1,hi); } }
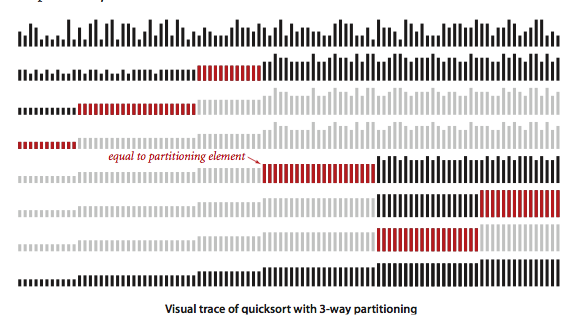
对于若干不同主键的随机数组，归并排序的时间复杂度是线性对数的，而三向切分快速排序是线性的。三向切分最坏的情况是所有键值都不同。当存在重复主键时，性能回避归并排序好很多。
