中国剩余定理（孙子定理）

中国剩余定理（CRT）的表述如下            注：需先了解扩展欧几里得与乘法逆元，链接点击打开链接

 

设正整数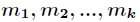两两互素，则同余方程组

 

                            

设M=∏ni=1mi,Mi=M/mi,Miti≡1(mod mi)

则方程组的通解形式即为：

x=∑ni=1aiMiti

在模M意义下只有一个解：

x=(∑ni=1aiMiti)mod M

问题：今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

简单点说就是，存在一个数x，除以3余2，除以5余三，除以7余二，然后求这个数。上面给出了解法。再明白这个解法的原理之前，需要先知道一下两个定理。

定理1：几个数相加，如果存在一个加数，不能被整数a整除，那么它们的和，就不能被整数a整除。

定理2：两数不能整除，若除数扩大（或缩小）了几倍，而被除数不变，则其商和余数也同时扩大（或缩小）相同的倍数（余数必小于除数）。

以上两个定理随便个例子即可证明！

现给出求解该问题的具体步骤：

1、求出最小公倍数

 lcm=3*5*7=105

2、求各个数所对应的基础数

（1）105÷3=35

 35÷3=11......2 //基础数35

（2）105÷5=21

 21÷5=4......1

 定理2把1扩大3倍得到3，那么被除数也扩大3倍，得到21*3=63//基础数63

3、105÷7=15

15÷7=2......1

定理2把1扩大2倍得到2，那么被除数也扩大2倍，得到15*2=30//基础数30

把得到的基础数加和（注意：基础数不一定就是正数）

35+63+30=128

4、减去最小公倍数lcm（在比最小公倍数大的情况下）

x=128-105=23

那么满足题意得最小的数就是23了，代码：

int CRT(int a[],int m[],int n)
{
    int M = 1;
    int ans = 0;
    for(int i=0; i<n; i++)
        M *= m[i];
    for(int i=0; i<n; i++)
    {
        int x, y;
        int Mi = M / m[i];
        extgcd(Mi, m[i], x, y);      //扩展欧几里得
        ans = (ans + Mi * x * a[i]) % M;    //x是对应的乘法逆元，a[i]是余数
    }
    return (ans+M)%M;
}