动态规划模板总结
动态规划:
通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
试用情况:
- 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。最优子结构性质为动态规划算法解决问题提供了重要线索。
- 无后效性。即子问题的解一旦确定,就不再改变,不受在这之后、包含它的更大的问题的求解决策影响。
- 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地查看一下结果,从而获得较高的效率。
具体还是要根据具体问题分析
一,01背包
有N件物品和一个容量为V的背包。第i件物品的重量是w[i],价值是c[i]。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。
关键是找出状态方程组,可知为dp[i][j]=max(dp[i-1][ j ],dp[i-1][j-w[i] ]+c[i]),所以可以写出代码
#include <iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int dp[3405][13000],c[3405],w[3405];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
scanf("%d%d",&w[i],&c[i]);
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
if(j<w[i])
dp[i][j]=dp[i-1][j];
else
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+c[i]);
}
}
printf("%d\n",dp[n][m]);
return 0;
}
然而可不可以优化一下呢,答案是可以的,可以考虑将其换成一维数组,即
dp[ j ]=max(dp[ j ],dp[ j-w[i] ]+c[i] );
#include <iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int dp[13000],c[3405],w[3405];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
scanf("%d%d",&w[i],&c[i]);
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;++i)
{
for(int j=m;j>=w[i];--j)
{
dp[j]=max(dp[j],dp[j-w[i]]+c[i]);
}
}
printf("%d\n",dp[m]);
return 0;
}
这样就可以简化算法了。
二:最长公共子序列
给定两个字符串,寻找这两个字串之间的最长公共子序列。
可知其状态方程为
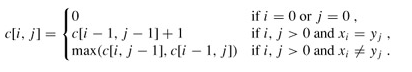
#include <iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<math.h>
using namespace std;
int dp[1001][1001];
int main()
{
string a,b;
cin>>a>>b;
memset(dp,0,sizeof(dp)); //初始化0
for(int i=1;i<=a.length();++i)
{
for(int j=1;j<=b.length();++j)
{
if(a[i-1]==b[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
cout<<dp[a.length()][b.length()];
return 0;
}
但此方程无法求出序列,需要另设一个数组c[ i ][ j ],这样就可以记录dp数组的值来源,然后就可以回溯找到序列
#include <iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<string>
#include<math.h>
using namespace std;
const int maxn=1002;
int dp[maxn][maxn],c[maxn][maxn];
string a,b;
void LCS( )
{
for(int i=1;i<=a.length();++i)
{
for(int j=1;j<=b.length();++j)
{
if(a[i-1]==b[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
c[i][j]=1;
}
else if(dp[i][j-1]>=dp[i-1][j])
{
dp[i][j]=dp[i][j-1];
c[i][j]=2;
}
else
{
dp[i][j]=dp[i-1][j];
c[i][j]=3;
}
}
}
}
void print(int i,int j)
{
if(i==0 || j==0)
return;
if(c[i][j]==1)
{
print(i-1,j-1);
cout<<a[i-1];
}
else if(c[i][j]==2)
print(i,j-1);
else
print(i-1,j);
}
int main()
{
cin>>a>>b;
memset(dp,0,sizeof(dp)); //初始化0
LCS();
cout<<dp[a.length()][b.length()]<<endl;
print(a.length(),b.length());
return 0;
}
三:最长递增子序列
介绍两种方法,
第一种:最长公共子序列法:先将原数组排序,然后将排序后的数组与原来数组比较最长公共子序列
#include<iostream>
#include<stdio.h>
#include<cmath>
#include<string>
#include<string.h>
#include<set>
#include<map>
#include <algorithm>
using namespace std;
/*方法1:将这n个数的序列排序之后,将最长递增子序列转变为LCS*/
int main() {
int n;
int A[100], B[100], res[100], len[105][105];
while (scanf("%d", &n) == 1) {
memset(res, 0, sizeof(res));
memset(len, 0, sizeof(len));
for (int i = 0; i < n; i++) {
scanf("%d", &A[i]);
B[i] = A[i];
}
sort(B, B + n);
int i, j, cnt = 0;
for (i = 1; i <= n; i++) {
for (j = 1; j <= n; j++) {
if(A[i-1] == B[j-1]) len[i][j] = 1 + len[i-1][j-1];
else len[i][j] = max(len[i-1][j], len[i][j-1]);
}
}
//输出任意一个最长公共子序列,倒叙遍历len数组
for (i = n, j = n; i > 0 && j > 0;) {
if (len[i][j] == len[i-1][j]) {
i--;
}
else if(len[i][j] == len[i][j-1]) {
j--;
}
else {
res[cnt++] = A[i-1];
i--;
j--;
}
}
printf("%d\n%d", cnt, res[cnt-1]);//输出这个最长公共子序列。
for (i = cnt - 2; i >= 0; i--) printf(" %d", res[i]);
printf("\n");
}
return 0;
}
第二种就是dp了,复杂度O(n^2),以dp[i]表示以i位结尾的最长递增子序列的长度。那么dp[i] = max(dp[i], dp[j]+1), j = 1, 2, 3,...,i-1。对于每个j<i遍历求出最大的dp[i],并用res[i] = j 来记录以i位结尾的最长递增子序列的前一位是谁,方便之后遍历输出子序列。
/* 输入数组,然后求最长递增子序列 */
#include <iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<string>
#include<math.h>
using namespace std;
const int maxn=1002;
int dp[maxn];
int LIS(int arr[],int len)
{
for(int i=0;i<len;++i)
dp[i]=1;
for(int i=1;i<len;++i)
{
for(int j=0;j<i;++j)
{
if(arr[i]>arr[j] && dp[i]<dp[j]+1)
dp[i]=dp[j]+1;
}
}
int maxx=0;
for(int i=0;i<len;++i)
if(maxx<dp[i])
maxx=dp[i];
return maxx;
}
int main()
{
int n,arr[maxn];
scanf("%d",&n);
for(int i=0;i<n;++i)
scanf("%d",&arr[i]);
int m=LIS(arr,n);
printf("%d\n",m);
return 0;
}
第三种就是利用二分的O(nlogn)的算法,但其只能求长度
#include<iostream>
#include<cstdio>
using namespace std;
int arr[50005];
int BinarySearch(int *arr,int value,int len)
{
int begin =0,end=len-1;
while(begin<=end)
{
int mid=begin+(end-begin)/2 ;
if(arr[mid]==value)
return mid;
else if(arr[mid]>value)
end=mid-1;
else
begin=mid+1;
}
return begin;
}
int LIS(int *arr,int len)
{
int a[len],n=1;
a[0]=arr[0];
for(int i=1;i<len;++i)
{
if(arr[i] > a[n-1])
{
a[n]=arr[i];
++n;
}
else
{
int pos = BinarySearch(a,arr[i],n);
a[pos]=arr[i];
}
}
return n;
}
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;++i)
scanf("%d",&arr[i]);
printf("%d\n",LIS(arr,n));
return 0;
}
四:最大子序列和
问题描述,给定一个连续序列,如{1,5,-2,9,7},让你求最大子序列和。
第一种方法,分治法,复杂度O(nlogn)
int maxsequence2(int a[], int l, int u)
{
if (l > u) return 0;
if (l == u) return a[l];
int m = (l + u) / 2;
/*求横跨左右的最大连续子序列左半部分*/
int lmax=a[m], lsum=0;
for (int i=m; i>=l; i--) {
lsum += a[i];
if (lsum > lmax)
lmax = lsum;
}
/*求横跨左右的最大连续子序列右半部分*/
int rmax=a[m+1], rsum = 0;
for (int i=m+1; i<=u; i++) {
rsum += a[i];
if (rsum > rmax)
rmax = rsum;
}
return max3(lmax+rmax, maxsequence2(a, l, m), maxsequence2(a, m+1, u)); //返回三者最大值
}
/*求三个数最大值*/
int max3(int i, int j, int k)
{
if (i>=j && i>=k)
return i;
return max3(j, k, i);
}
第二种是线性O(n)
int maxsequence3(int a[], int len)
{
int maxsum, maxhere;
maxsum = maxhere = a[0]; //初始化最大和为a【0】
for (int i=1; i<len; i++) {
if (maxhere <= 0)
maxhere = a[i]; //如果前面位置最大连续子序列和小于等于0,则以当前位置i结尾的最大连续子序列和为a[i]
else
maxhere += a[i]; //如果前面位置最大连续子序列和大于0,则以当前位置i结尾的最大连续子序列和为它们两者之和
if (maxhere > maxsum) {
maxsum = maxhere; //更新最大连续子序列和
}
}
return maxsum;
}五:编辑距离
给定两个字符串,s1和s2,让你求通过插入删除修改等操作使两个字符串相等的最小次数(距离)
显然可以有如下动态规划公式:
- if i == 0 且 j == 0,dp(i, j) = 0
- if i == 0 且 j > 0,dp(i, j) = j
- if i > 0 且j == 0,dp(i, j) = i
- if i ≥ 1 且 j ≥ 1 ,dp(i, j) == min{dp(i-1, j) + 1, dp(i, j-1) + 1,dp(i-1, j-1) + temp },当第一个字符串的第i个字符不等于第二个字符串的第j个字符时,temp= 1;否则,temp = 0。
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std ;
const int maxn=10005;
char str1[maxn],str2[maxn];
int dp[maxn][maxn];
int editdistance(char *str1,char *str2)
{
int len1=strlen(str1);
int len2=strlen(str2);
for(int i=0;i<=len1;++i)
dp[i][0]=i; //第二个字符串长度为0,需要操作i次
for(int j=0;j<=len2;++j)
dp[0][j]=j;
for(int i=1;i<=len1;++i)
{
for(int j=1;j<=len2;++j)
{
int temp;
if(str1[i-1]==str2[j-1])
temp=0;
else
temp=1;
dp[i][j]=min(min(dp[i-1][j]+1,dp[i][j-1]+1),dp[i-1][j-1]+temp);
} //求三个中最小的
}
return dp[len1][len2];
}
int main()
{
cin>>str1>>str2;
int t=editdistance(str1,str2);
cout<<t;
return 0 ;
}
六:最优三角剖分
给定凸多边形P,以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分,使得该三角剖分中诸三角形上权之和为最小。
状态方程为:其中w( v(i-1)v(k)v(j) )=g[i-1][k]+g[k][j]+g[i-1][j];

#include<iostream>
#include<sstream>
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std ;
const int M= 1000 + 5 ;
int n ;
int s[M][M] ; //记录路径
double m[M][M],g[M][M]; //记录最优解以及存储权值
void Convexpolygontriangulation()
{
for(int i = 1 ;i <= n ; i++) // 初始化
{
m[i][i] = 0 ;
s[i][i] = 0 ;
}
for(int d = 2 ;d <= n ; d++) // 枚举点的个数
for(int i = 1 ;i <= n - d + 1 ; i++) // 枚举起始点
{
int j = i + d - 1 ; // 终点
m[i][j] = m[i+1][j] + g[i-1][i] + g[i][j] + g[i-1][j] ;
s[i][j] = i ;
for(int k = i + 1 ;k < j ; k++) // 枚举中间点
{
double temp = m[i][k] + m[k+1][j] + g[i-1][k] + g[k][j] + g[i-1][j] ;
if(m[i][j] > temp)
{
m[i][j] = temp ; // 更新最优值
s[i][j] = k ; // 记录中间点
}
}
}
}
void print(int i , int j) // 输出所有的弦
{
if(i == j) return ;
if(s[i][j]>i)
cout<<"{v"<<i-1<<"v"<<s[i][j]<<"}"<<endl;
if(j>s[i][j]+1)
cout<<"{v"<<s[i][j]<<"v"<<j<<"}"<<endl;
print(i ,s[i][j]);
print(s[i][j]+1 ,j);
//cout<<"{ v"<<i-1<<" , v"<<s[i][j]<<" , v"<<j<<" }"<<endl; //输出所有剖分后的三角形
}
int main()
{
int i,j;
cout << "请输入顶点的个数 n:";
cin >> n;
n-- ;
cout << "请依次输入各顶点的连接权值:";
for(int i = 0 ;i <= n ; i++) // 输入各个顶点之间的距离
for(int j = 0 ;j <= n ; j++)
cin>>g[i][j] ;
Convexpolygontriangulation();
cout<<m[1][n]<<endl;
print(1 ,n); // 打印路径
return 0 ;
}
待更新... ...



 浙公网安备 33010602011771号
浙公网安备 33010602011771号