全排列解析【递归方法】

定义

         从n个元素中取出m个元素进行排列，当n=m时这个排列被称为全排列。

递归法

          我们要对前n个数进行全排列，那么首先我们可以发现第一位数可以是1~n中的任意一位，枚举第一位数的n种可能，然后我们就可以再去求剩下n-1位，确定第二位后再递归剩下的n-2位，一直递归即可求解。

步骤

1.首先枚举全排列第一个位置的元素，即让其分别为1,2,3……n。

2.接着开始枚举第二个位置的元素，一直递归，直到最后一个元素。

3.记得还原数组，否则数组的值会被改变，影响后面排列。

4.如果找到一个排列，就输出。

代码

#include<cstdio>
#include <iostream>
using namespace std;
void perm(int *a,int p,int q)   //其中初始时p指向数组头元素的下标，q指向尾部元素的下标
{
    if(p==q)                    //说明已经找到一个排列，输出他们
    {
        for(int i=0;i<=q;++i)
            printf("%d ",a[i]);
        printf("\n");
    }
    else
    {
        for(int i=p;i<=q;++i)    //枚举前缀
        {
            swap(a[i],a[p]);     //交换值，即前缀的值
            perm(a,p+1,q);
            swap(a[i],a[p]);     //数组还原
        }
    }
}

int main()
{
    int a[4]={1,2,3,4};
    perm(a,0,3);
    return 0;
}

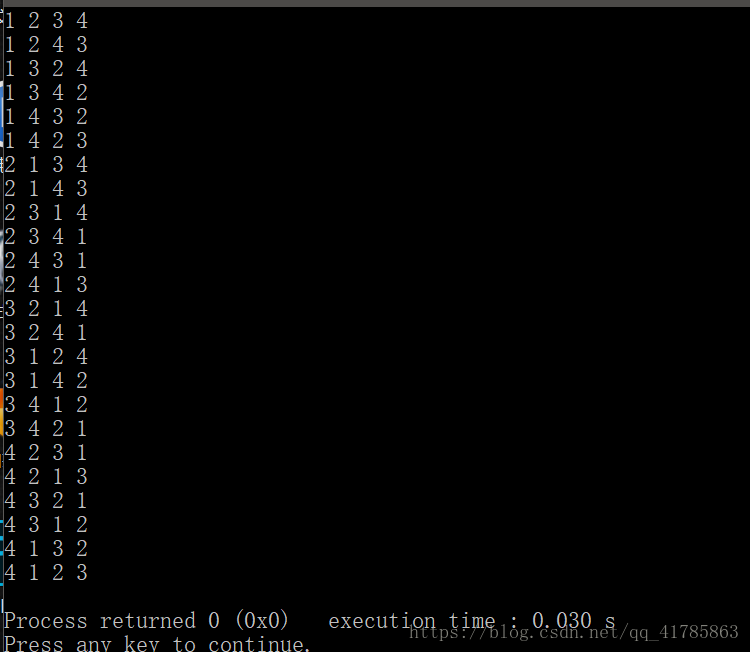
结果

备注：如果还有疑问或者想了解更多请戳链接看视频讲解点击打开链接