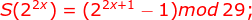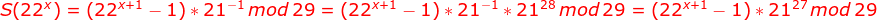HDU 1452 Happy 2004（因数和+费马小定理+积性函数）

Happy 2004


Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2183    Accepted Submission(s): 1582


Problem Description
Consider a positive integer X,and let S be the sum of all positive integer divisors of 2004^X. Your job is to determine S modulo 29 (the rest of the division of S by 29).

Take X = 1 for an example. The positive integer divisors of 2004^1 are 1, 2, 3, 4, 6, 12, 167, 334, 501, 668, 1002 and 2004. Therefore S = 4704 and S modulo 29 is equal to 6.

 

Input
The input consists of several test cases. Each test case contains a line with the integer X (1 <= X <= 10000000). 

A test case of X = 0 indicates the end of input, and should not be processed.

 

Output
For each test case, in a separate line, please output the result of S modulo 29.

 

Sample Input
1
10000
0
 

Sample Output
6
10
 

Source
ACM暑期集训队练习赛（六） 
 

Recommend
lcy   |   We have carefully selected several similar problems for you:  1695 1788 1060 1370 1211 

题解：

1.积性函数：函数f如果满足对于任意两个互质的正整数m和n，均有f(mn)=f(m)f(n)，就称f为积性函数（或乘性函数）。如果对于任意两个正整数m和n，均有f(mn)=f(m)f(n)，就称为完全积性函数。

2.因数和函数：{\color{Red} S(p^{x})=1+p^{1}+p^{2}+...+p^{x}=(p^{x+1}-1)/(p-1)}

3.因数和函数为积性函数，结合费马小定理:

{\color{Red} S(2004^{x})=S(2^{2x})*S(3^{x})*S(167^{x})mod\, 29=S(2^{2x})*S(3^{x})*S(22^{x})mod\, 29}

{\color{Red} S(2^{2x})=(2^{2x+1}-1)mod\, 29;}

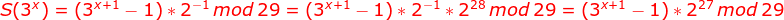
{\color{Red} S(3^{x})=(3^{x+1}-1)*2^{-1}\, mod\,29=(3^{x+1}-1)*2^{-1}*2^{28}\, mod\,29=(3^{x+1}-1)*2^{27}\, mod\,29} 

{\color{Red} S(22^{x})=(22^{x+1}-1)*21^{-1}\, mod\,29=(22^{x+1}-1)*21^{-1}*21^{28}\, mod\,29=(22^{x+1}-1)*21^{27}\, mod\,29}

#include<iostream>
using namespace std;
int mul(int a,int x){
        int ans=1;
        while(x){
                if(x&1)
                        ans=a*ans%29;
                x>>=1;
                a=a*a%29;
        }
        return ans;
}
int main()
{
        int x;
        while(~scanf("%d",&x)&&x)
        {
                int ans1=(mul(2,2*x+1)-1)%29;
                int ans2=(mul(3,x+1)-1)%29*mul(2,27)%29;
                int ans3=(mul(22,x+1)-1)%29*mul(21,27)%29;
                printf("%d\n",ans1*ans2*ans3%29);
        }
        return 0;
}

 

posted @ 2018-12-21 10:10  aeipyuan  阅读(115)  评论(0)  编辑  收藏  举报