算法学习:矩阵快速幂/矩阵加速
1.前言
其实本质上来说,矩阵快速幂或是矩阵加速的题目比较的模板化一些,大体上都是属于我们要先写出来一个递推式子(或者是我们需要递推的式子),然后由于递推的次数过大,1e18之类的,会导致复杂度的飚升,所以我们会用到矩阵来帮我们快速处理。
另外,从题目的类型上大概是分为两类,一类是线性递推式,再利用矩阵加速处理;另外一类就是图上的问题,一般点数较小,可能100不到,然后对边有限制要求之类的,例如需要走T步,T的范围是[1,1e18],此时我们也可以用矩阵加速处理。
本篇的主要内容以矩阵加速为主,矩阵快速幂的内容会比较草率。
2.矩阵快速幂
我们来大概了解一下矩阵快速幂,首先要确保我们是会快速幂的。以下贴出来快速幂的代码:
int kuai(int a,int b){
int tem=1;
while(b){if(b%2) tem=tem*a; a=a*a,b/=2;}
return tem;
}
具体了解快速幂请百度,而矩阵的运算和实数的运算在结合律上是一致的,所以我们完全可以套用快速幂的形式写出来矩阵快速幂:Mat是我设的矩阵的结构体
static Mat kuai(Mat A, int b) {
Mat tem(A.n, A.m, 1, A.st);//参数分别代表,行,列,初始化内容,下标从1或者0开始
while (b) { if (b % 2) tem = tem * A; b = b / 2, A = A * A; }
return tem;
}
另外此处贴上我的矩阵的板子,后面的代码展示中就省略了板子:
struct Mat {
int a[130][130];
int n, m, st;
Mat(int n_, int m_, int fl = 0, int st_ = 1) {
n = n_, m = m_, st = st_;
if (!fl) rep(i, st, n) rep(j, st, m) a[i][j] = 0;
if (fl == INF) rep(i, st, n) rep(j, st, m) a[i][j] = INF;
if (fl == 1) rep(i, st, n) rep(j, st, m) a[i][j] = (i == j);
}
int* operator [] (int x) { return a[x]; }
Mat operator * (Mat b) {
Mat res(n, b.m, 0, b.st);//记得赋值
rep(i, st, n) rep(j, st, b.m) rep(k, st, m) {
res[i][j] += a[i][k] * b[k][j] % mod;
res[i][j] %= mod;
}
return res;
}
Mat operator + (Mat b) {
Mat res(n, b.m, 0, b.st);//记得赋值
rep(i, st, n) rep(j, st, b.m) {
res[i][j] = a[i][j] + b[i][j];
res[i][j] %= mod;
}
return res;
}
static Mat kuai(Mat A, int b) {
Mat tem(A.n, A.m, 1, A.st);
while (b) { if (b % 2) tem = tem * A; b = b / 2, A = A * A; }
return tem;
}
//指数从0开始的求和
static Mat kuai_sum(Mat A, int b) {
Mat tem(A.n, A.m, 1, A.st); Mat sum = tem;
while (b) {
if (b % 2) tem = sum + tem * A;
sum = sum + sum * A; A = A * A, b /= 2;
}
return tem;
}
void out() {
rep(i, st, n) { rep(j, st, m) cout << a[i][j] << " "; cout << endl; }
}
};
3.矩阵加速
第一类:线性递推式加速
学习一个东西是什么,以及怎么用,最好的办法就是去看一道经典的例题。
下面来看一道矩阵加速的板题:洛谷P1962
题目描述:
请你求出 \(F_n \bmod 10^9 + 7\) 的值。
对于 \(100\%\) 的数据,\(1\le n < 2^{63}\)。
题解:
这里我们已经有了递推式,\(F_{n-1} + F_{n-2} = F_{n}\),正常我们只需要这样一直递推下去就好了,但是n的数据范围是2的63次方,所以我们不得不考虑别的办法:我们先把这两个式子写成矩阵的形式
\(I_1=\begin{bmatrix}F_{n-1} & F_{n-2} \end{bmatrix}\)
此时我们假设一下,这个矩阵需要乘上一个什么矩阵可以变成
\(I_2=\begin{bmatrix}F_{n} & F_{n-1} \end{bmatrix}\)
在草稿纸上写写画画,我们就发现
\(A=\begin{bmatrix}1 & 1 \\ 1 & 0 \end{bmatrix}\)
当\(I_1*A\)就会变成\(I_2\),而且,这个矩阵都是常数,且任意的一个\(I_{i}\)矩阵乘上它都会满足变成\(I_{i+1}\)
所以我们从\(I_{i}\)一直乘A,可以变成我们想要的\(I_{n}\),此时在利用之前学习的矩阵快速幂,我们就可以在\(log\)的时间里求出来我们最后的\(F_{n}\),另外再提一句,这个A矩阵的构建,是我们要先写出来\(I_1\)(我们本身有的递推式),然后将这个递推式子的下标都+1,这是我们的目标矩阵,根据这两个来倒推出我们的转移矩阵,也就是A矩阵。我们会发现当[1,1]和[2,1]的位置都填1,就是我们斐波那契数列本身的递推式子,然后\(F_{n-1}\)我们直接在[1,2]的位置写1,再次利用我们上一个矩阵本身就有的即可。
此处贴上代码:
int n, m, T;
signed main() {
read(), kuaidu();
int st, ed;
cin >> n;
if (n == 1 || n == 2) cout << 1 << endl;
else {
Mat A(1, 2);
A[1][1] = 1, A[1][2] = 1;
Mat base(2, 2);
base[1][1] = base[1][2] = base[2][1] = 1;
A = A * Mat::kuai(base, n - 2);
cout << A[1][1] << endl;
}
return 0;
}
第二类:在图上的应用
我们还是接着来看一道例题:洛谷P2233
题目描述
在长沙城新建的环城公路上一共有 \(8\) 个公交站,分别为 A、B、C、D、E、F、G、H。公共汽车只能够在相邻的两个公交站之间运行,因此你从某一个公交站到另外一个公交站往往要换几次车,例如从公交站 A 到公交站 D,你就至少需要换 \(3\) 次车。
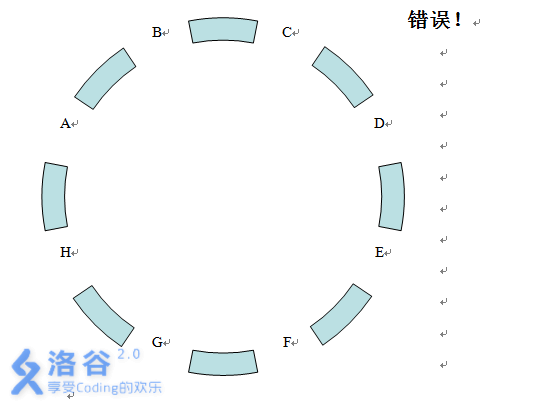
图片来自洛谷
Tiger 的方向感极其糟糕,我们知道从公交站 A 到公交 E 只需要换 \(4\) 次车就可以到达,可是 tiger 却总共换了 \(n\) 次车,注意 tiger 一旦到达公交站 E,他不会愚蠢到再去换车。现在希望你计算一下 tiger 有多少种可能的乘车方案。
输入格式
仅有一个正整数 \(n\),表示 tiger 从公交车站 A 到公交车站 E 共换了 \(n\) 次车。
\(4\le n\le10^7\)。
题解:
首先这个题我们很显然的能够知道,转化成图上就是有8个点,8个点只有互相相邻的可以抵达,我们建立一个邻接矩阵,其中给相邻的能到达的赋值为1,(除了E这个点,因为到达了就不会再去别的车站了),E车站向其他车站的赋值是0。因为这里n的数值很大,所以我们还是可以进行矩阵加速。
这里稍微浅扯一下关于这里为什么图上的邻接矩阵我们依旧可以进行矩阵加速,先看矩阵乘法的代码实现:
Mat operator * (Mat b) {
Mat res(n, b.m, 0, b.st);//记得赋值
rep(i, st, n) rep(j, st, b.m) rep(k, st, m) {
res[i][j] += a[i][k] * b[k][j] % mod;
res[i][j] %= mod;
}
return res;
}
这里我们中间的式子,可以抽象的理解成是\(i\)到\(k\)的路径方案数乘以\(k\)到\(j\)的路径方案数,加到\(res[i][j]\)里面,此刻\(res[i][j]\)代表的就是我们将两个矩阵相乘后(意义上是步数相加)的方案数,原本这个邻接矩阵代表着我们走1步的方案数,所以再进行矩阵快速幂即可。
signed main() {
read(), kuaidu();
int t;
cin >> n;
Mat A(7, 7);
rep(i, 0, 7) {
int x = i, y = (i + 1) % 8, z = (i - 1 + 8) % 8;
A[x][z] = 1;
A[x][y] = 1;
}
rep(i, 0, 7) A[4][i] = 0;
Mat dp = Mat::kuai(A, n);
// dp.out();
// A.out();
cout << dp[0][4] << endl;
return 0;
}
到此为止,我们算是将矩阵加速的基础题过了一遍,本人剩下的训练内容来自洛谷的矩阵题单,可以自行搜索。
我在这里面的题当中抽出来几道讲讲:
4.习题
4.1 P4159 [SCOI2009] 迷路
题目描述
该有向图有 \(n\) 个节点,节点从 \(1\) 至 \(n\) 编号,windy 从节点 \(1\) 出发,他必须恰好在 \(t\) 时刻到达节点 \(n\)。
现在给出该有向图,你能告诉 windy 总共有多少种不同的路径吗?
答案对 \(2009\) 取模。
注意:windy 不能在某个节点逗留,且通过某有向边的时间为该边长度。
输入格式
第一行包含两个整数,分别代表 \(n\) 和 \(t\)。
第 \(2\) 到第 \((n + 1)\) 行,每行一个长度为 \(n\) 的字符串,第 \((i + 1)\) 行的第 \(j\) 个字符 \(c_{i, j}\) 是一个数字字符,若为 \(0\),则代表节点 \(i\) 到节点 \(j\) 无边,否则代表节点 \(i\) 到节点 \(j\) 的边的长度为 \(c_{i, j}\)。
- 对于 \(100\%\) 的数据,保证 \(2 \leq n \leq 10\),\(1 \leq t \leq 10^9\)。
题解:
这里我们知道,如果有向边的长度是1的话,就直接变成模板题了,但是长度是权值,我们不能这么做。细心一点,会发现因为输入的是字符串,所以长度最大就是9,边权的范围是在1-9之间。我们可以像网络流那样来进行拆点,每一个点\(i\)拆成9个点,\(i_1,i_2,...,i_9\),而我们每一次从一个点走,都是从\(i_1\)走,举个例子,我们从\(i\)到\(j\),权值是3,我们可以建立\(i_1 -> j_3\),权值是1的边,然后再从\(j_3->j_2->j_1\),每一条边权值都是1,这样用拆点的方法解决了权值的问题,剩下的就和正常的板子题一样了。
int fan(int x, int y) {
return (x - 1) * 10 + y;
}
signed main() {
read(), kuaidu();
cin >> n >> m;
Mat A(100, 100);
rep(i, 1, n) {
string S; cin >> S;
int len = S.size();
rep(j, 0, len - 1) {
if (S[j] == '0') continue;
int x = fan(i, 1), y = fan(j + 1, (S[j] - '0'));
A[x][y] = 1;
}
}
rep(i, 1, n) {
rep(j, 2, 10) A[fan(i, j)][fan(i, j - 1)] = 1;
}
A = Mat::kuai(A, m);
cout << A[fan(1, 1)][fan(n, 1)] << endl;
return 0;
}
4.2 P3216 [HNOI2011] 数学作业
题目描述
给定正整数 \(n,m\),要求计算 \(\text{Concatenate}(n) \bmod \ m\) 的值,其中 \(\text{Concatenate}(n)\) 是将 \(1 \sim n\) 所有正整数 顺序连接起来得到的数。
例如,\(n = 13\),\(\text{Concatenate}(n) = 12345678910111213\)。小 C 想了大半天终于意识到这是一道不可能手算出来的题目,于是他只好向你求助,希望你能编写一个程序帮他解决这个问题。
对于 \(100\%\) 的数据,\(1\le n \le 10^{18}\),\(1\le m \le 10^9\)。
题解:
这里我们先用递推的形式,大概能写出来,当i是个位数的时候,我们只需要\(F_{i-1}\)乘10,再加上\(i\)就好了,但是我们发现当i是两位数的时候,我们就是乘以100而不是10,以此类推,当我们是k位数时,我们需要乘\(10^k\),所以这里我们没有办法像之前那样,找到转移矩阵一口气直接乘到最后就好了,我们可以先写出来当i是个位数时的转移矩阵,然后需要每当位数+1的时候我们的转移矩阵也更新,将10变成100,再变成1000...,就可以了,时间复杂度会比之前的log多一个lg出来。
(顺便一提,这个题需要开unsigned long long,并且不要使用std的pow函数,返回类型是int,还有判断位数的时候不要使用log10函数,要手写!!不要问我怎么知道的qwq)
int kuai(int a, int b) {
int tem = 1;
while (b) {
if (b % 2) tem = tem * a;
a = a * a, b /= 2;
}
return tem;
}
int fan(int x) {
int cnt = 0;
while (x) {
x /= 10;
cnt++;
}
return cnt;
}
signed main() {
read(), kuaidu();
// cout << log10(124551) << endl;
cin >> n >> mod;
Mat base(3, 3);
base[1][1] = 10, base[2][1] = 1, base[2][2] = 1, base[3][2] = 1, base[3][3] = 1;
Mat dp(1, 3);
dp[1][1] = 0, dp[1][2] = 1, dp[1][3] = 1;
int k = fan(n) - 1;
int las = n - kuai(10, k);
int q = 1;
while (1) {
base[1][1] = q * 10 % mod;
q *= 10;
if (q <= n) { dp = dp * Mat::kuai(base, q - q / 10); }
else break;
}
dp = dp * Mat::kuai(base, las + 1);
cout << dp[1][1] << endl;
return 0;
}
关于矩阵加速的内容先写这么多,之后还会再更一篇矩阵的题,是2024杭电7的循环图。就是因为这个题才让我开始补矩阵的-_-


 浙公网安备 33010602011771号
浙公网安备 33010602011771号