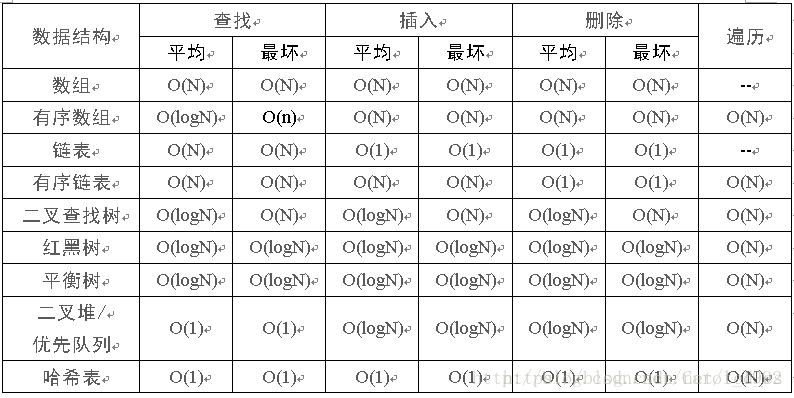
常用算法时间空间复杂度

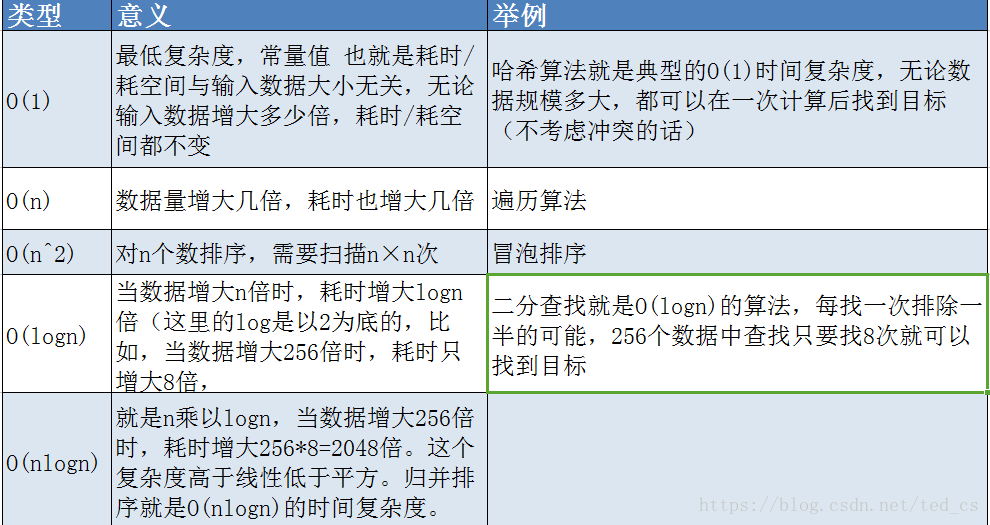
在描述算法复杂度时，经常用到O(1), O(n), O(logn), O(nlogn)来表示对应复杂度程度, 不过目前大家默认也通过这几个方式表示空间复杂度 。

那么，O(1), O(n), O(logn), O(nlogn)就可以看作既可表示算法复杂度，也可以表示空间复杂度。

大O加上（）的形式，里面其实包裹的是一个函数f(),O（f()）,指明某个算法的耗时/耗空间与数据增长量之间的关系。其中的n代表输入数据的量。

 

 

 

若aⁿ=b(a>0，且a≠1)，称为a的n次幂等于b。在这里，a叫作底数，n叫作指数，

b叫作以a为底的n次幂。

若写成对数形式就是：

 

在这里，a仍然叫作底数，b叫作真数，而n叫作以a为底b的对数。

由此可见，指数和对数都是n，即它们是指同一个东西，只是在不同场合叫不同的名字。

特别地，我们称以10为底的对数叫做常用对数（common logarithm），并记为lg。

称以无理数e（e=2.71828...）为底的对数称为自然对数（natural logarithm），并记为ln。