P7706 文文的摄影布置 题解

合集 - 题解(15)

1.[ABC347C] Ideal Holidays题解2024-03-312.《扶苏的问题》题解2024-06-023.[ABC366C] Balls and Bag Query 题解2024-08-124.[ABC366D] Cuboid Sum Query 题解2024-08-12

5.P7706 文文的摄影布置 题解2024-08-21

6.[ABC370C] Word Ladder 题解2024-09-087.P11020 「LAOI-6」Radiation 题解2024-09-088.P11019 「LAOI-6」[太阳]] 请使用最新版手机 QQ 体验新功能 题解2024-09-089.[ABC371D] 1D Country 题解2024-09-1510.[ABC371D] 1D Country 线段树解法2024-09-1511.P1955 程序自动分析 题解2024-10-1812.[ABC376E] Max × Sum 题解2024-10-2013.[ABC379D] Home Garden 题解2024-11-1014.P11276 第一首歌 题解2024-11-1515.[ABC380C] Move Segment 题解2024-11-18

收起

P7706 文文的摄影布置 题解

原题

读完题，发现是线段树。单点修改+区间查询。

不过查询的值有些奇怪，就是了，我们考虑用线段树维护这个 ψ 值(下称待求值)。

对于一个区间的待求值，大概有四种情况：

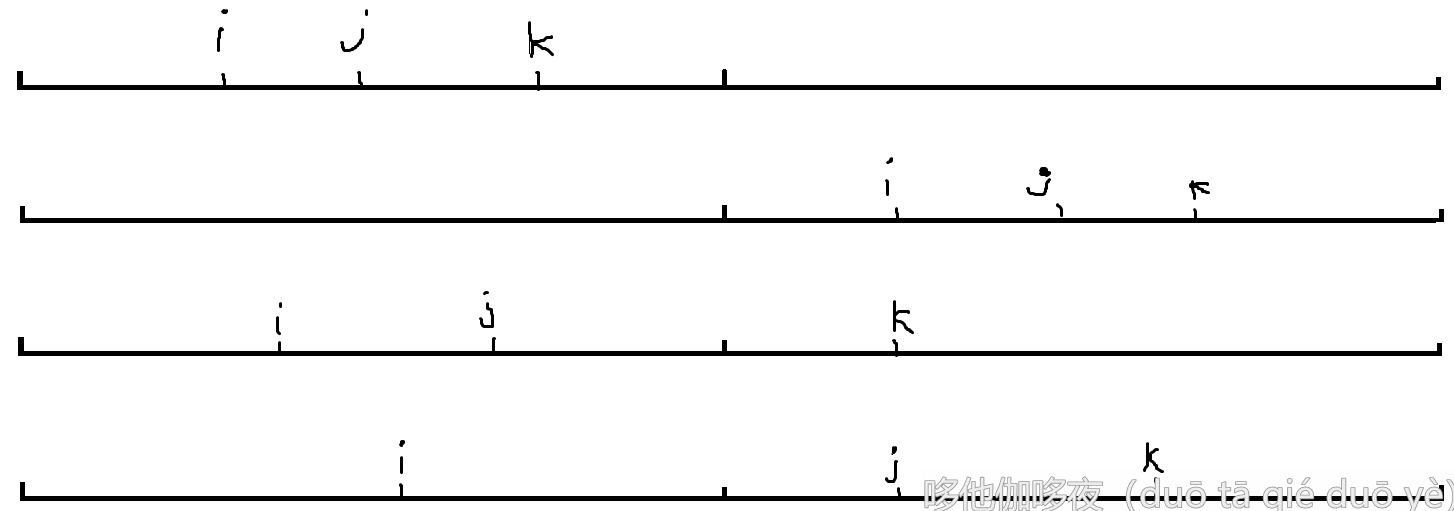
如上图四种情况分别为：

1. 待求值最大值在左区间
2. 待求值最大值在右区间
3. $a_i\mathrm{与}{b}_j$ 在左区间
4. $b_j\mathrm{与}{a}_k$ 在右区间

考虑合并的方式：

对于1,2，返回左右区间的较大的待求值。

对于3,4，维护左右区间的 $lt$ 与 $rt$ ,分别代表，较大的 $a_i-b_j$ 及 较大的 $a_k{-}_j$ ，更新时加上另一侧较大值即可。

由此，得出线段树结构体需要维护的值有：$maxx,minn,lt,rt,mx$ ,分别为最大的 $a$ ，最小的 $b$ ，较大的 $a_i-b_j$ 及 较大的 $a_k{-}_j$ ，和本区间的最大待求值。

于是可得代码：

#include <bits/stdc++.h>
#define seq(q, w, e) for (int q = w; q <= e; q++)
#define ll long long
using namespace std;
const int maxn = 5e5+10;
const ll inf=-1e8-10;
struct pect{
    ll s,b;                                          //存图片
}a[maxn];
struct node{
    ll maxx,minn;                                    //maxx为区间a最大，minn为区间b最小
    ll lt,rt,mx;                                     //lt为区间 min(bj)-ai,rt为区间 ak-min(bj)
}tree[maxn<<2];

ll ls(ll p){return p<<1;}
ll rs(ll p){return p<<1|1;}

node up_date(node a,node b){
    node p;
    p.maxx=max(a.maxx,b.maxx);
    p.minn=min(a.minn,b.minn);
    p.lt=a.maxx-b.minn;
    p.rt=b.maxx-a.minn;
    p.lt=max(p.lt,max(a.lt,b.lt));                //三种情况取最大
    p.rt=max(p.rt,max(a.rt,b.rt));
    p.mx=max(a.lt+b.maxx,b.rt+a.maxx);            //情况取最大
    p.mx=max(p.mx,max(a.mx,b.mx));
    return p;
}

void push_up(ll p){
    tree[p]=up_date(tree[ls(p)],tree[rs(p)]);
}

void build(ll p,ll pl,ll pr){
    if(pl==pr){
        tree[p].maxx=a[pl].s;
        tree[p].minn=a[pl].b;
        tree[p].lt=tree[p].rt=tree[p].mx=inf;
        return;
    }
    ll mid=(pl+pr)>>1;
    build(ls(p),pl,mid);
    build(rs(p),mid+1,pr);
    push_up(p);
}

void change(ll x,ll d,ll p,ll pl,ll pr,ll op){
    if(pl==pr){
        if(op==1) tree[p].maxx=d;
        if(op==2) tree[p].minn=d;
        return;
    }
    ll mid=(pl+pr)>>1;
    if(x<=mid) change(x,d,ls(p),pl,mid,op);
    else change(x,d,rs(p),mid+1,pr,op);
    push_up(p);
}

node query(ll l,ll r, ll p,ll pl,ll pr){
    if(l<=pl&&r>=pr)
        return tree[p];
    ll mid=(pl+pr)>>1;
    if(l>mid) return query(l,r,rs(p),mid+1,pr);
    if(r<=mid) return query(l,r,ls(p),pl,mid);
    return up_date(query(l,r,ls(p),pl,mid),query(l,r,rs(p),mid+1,pr));
}

ll n,m,op;

signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin>>n>>m;
    seq(i,1,n){
        cin>>a[i].s;
    }
    seq(i,1,n){
        cin>>a[i].b;
    }
    build(1,1,n);
    while(m--){
        int x,y;
        cin>>op>>x>>y;
        if(op==1){
            change(x,y,1,1,n,1);
        }
        if(op==2){
            change(x,y,1,1,n,2);
        }
        if(op==3){
            cout<<query(x,y,1,1,n).mx<<endl;
        }    
    }
    return 0;
}