排列组合:公式及推导
引入
定义:
排列:从指定个数的元素中取出指定个数的元素进行排序;(考虑元素的顺序)
组合:从给定个数的元素中仅仅取出指定个数的元素;(不考虑元素的顺序)
加法&乘法原理
加法原理:
完成一个工程可以有 类办法, 代表第 类方法的数目。则完成这件事共有 种不同的方法。
乘法原理:
完成一个工程需要 个步骤, 代表第 个步骤的不同方法的数目。那么完成这个工程共有 种不同的方法。
排列与组合基础
排列数:
从 个不同的元素中,任取 个元素按照一定的顺序排成一列,叫做从 个不同元素中 个元素的一个排列;从 个不同元素中取出 个元素的所有排列个数,叫做从 个元素中取出 个元素的排列数,用符号 (或者是 )表示。
排列的计算公式如下:
代表 的阶乘,即 。
公式可以这样理解: 个人选 个来排队,队长为 ( ),第一个位置可以选的人为 个,第二个位置可以选的人为 个,以此类推,第 个(最后一个)可以选 个,得:
全排列: 个人来排队,队长为 。第一个位置 可以选 个,第二个位置可以选 个,依此类推得:
全排列是排列数的一个特殊情况。
组合数:
从 个不同元素中,任取 个元素组成一个集合,叫做从 个不同元素中取出 个元素的一个组合;从 个不同元素中q取出 个元素组成的所有组合的个数,叫做从 个不同元素中取出 个元素的组合数,用符号 来表示,读作 。
组合数计算公式:
如何理解上述公式?考虑 个人选 个出来 ,不排队,不在乎顺序。如果关心顺序,则为 ,若不关心那么就要除掉重复,那么重复了多少?同样 个人,还要 得 ,所以得:
组合数也常用 表示,即 。
组合数也被称为 ,下文会阐述其联系。
特别的,当 时, 。
插板法
插板法是用于求一类给相同元素分组的方案数的一种技巧,也可用于求一类线性方程组的解的组数。
正整数和的题目
:现有 个完全相同的元素,要求将其分为 组,保证每组至少有一个元素,共有多少种分法?
对于这个问题我们可以抽象理解为在 个空隙中插入 块隔板,将 整个长队分为 部分,两块隔板不能相邻。这样就变成了经典的组合数问题。可得
其本质是求 的正整数解的组数。
非负整数和的题目
:若允许为空呢?
此时没法插板了,因为可能会出现很多板子插到一个空的情况,非常不好计算。因此,我们考虑加以约束,使其转化为有限制的 。先借 个元素,平均分配到 组,在 个元素形成的 个空里插板,则
由于元素是完全相同的,在分完组后,从每一组中都拿走一个,对结果是完全没有影响的,也就是结果相等。
其本质是求 的非负整数解的组数。
不同下界整数和的题目
:若每组至少有 个元素呢?
此时,对于插板法,会导致版的间隔增大,不好计算。同 ,看看如何转化为 。先将 个元素压入各组,则转化为在 个空隙中插板。
不相邻的排列
在 中选 个,这 个数中任何两个数都不相邻的组合由有 种。
二项式定理
二项式定理阐明了一个展开式的系数:
采用数学归纳法:
手演一遍,会发现对于 当 时,此时等于 ,以此类推,分别为
为一时:
为二时:
为三时:
现在可以找一下规律。
我们将其写作一个塔的样子:
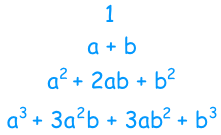
现在只看系数:
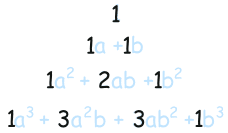
是不是非常熟悉?
是的,这便是杨辉三角:
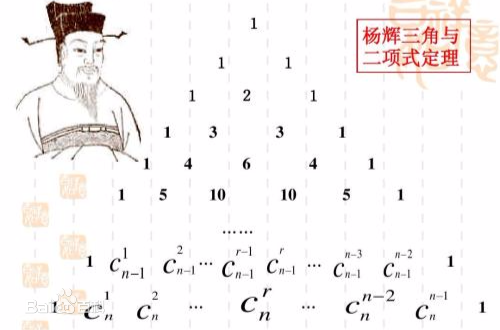
杨辉三角是二项式定理的一种图形上的显式呈现,杨辉三角向我们呈现了组合的一个性质,即:
不仅如此,对于 的展开式来说,其中的各项系数依次对应杨辉三角的第 行中的每一项 (二项式定理)。
二项式系数
二项式系数可以排列成帕斯卡三角形(杨辉三角形)。若将二项式系数排成一行,在从上向下排列,则构成帕斯卡三角形。
二项式系数常见于各数学领域中,尤其是组合数学。事实上,其可以理解为从 个相异的的元素中选出 个元素的方法数。二项式系数的定义可以推广至 是复数的情况,而且仍被称为二项式系数。
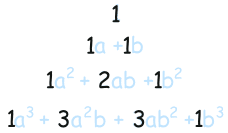




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异