搜索
搜索
发现上一篇写的有点简略，于是重发一遍吧；
（BFS）待更新（to be continue）；
概述：
主要分为DFS与BFS；
本质上为暴力枚举，但是要充分发挥人类智慧
当F为栈时，则算法为DFS（先进后出，即回溯的过程）；
当F为队列时，则算法为BFS（先进先出，先处理的为相近的节点）；
结束条件：点集F为空时；
具体处理看题目操作；
DFS与BFS不同：
DFS: 操作步骤字典序最小的解
BFS:操作步骤最小的解
DFS（深度优先搜索）
顾名思义，深度优先搜索，即搜索的一种；
在搜索时，优先向下一深度搜索，可以被用作实现回溯算法。
主要实现方法一种是依靠递归函数，另一种为栈；
（回溯算法）：
在枚举时，枚举所有可能的选项，然后判断是否合法。合法则填写下一个选项，后继续。
否则就没有继续的必要了，不用再往下枚举了，而是尝试更换上一个选项的填空（即回溯）
继续枚举；
这种算法称作回溯算法，常用深度优先搜索来实现；
流程框架：
删除部分与蓝字部分为递归DFS与一般搜索不同之处；
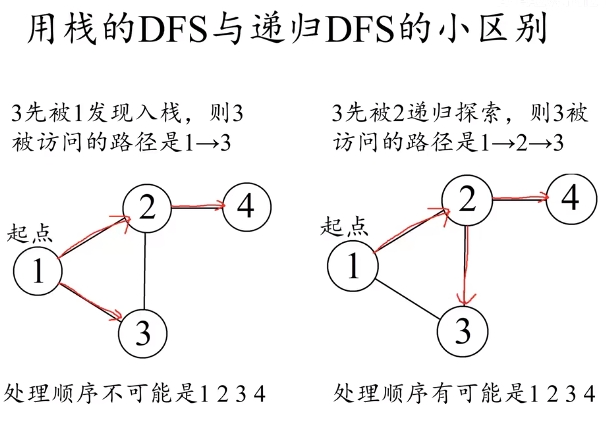
虽然在结果上应该没有问题，但具体的代码方面两者可能大有不同
遍历经历：
若使用DFS的搜索方法；
在下图树各点中的遍历方法为：
0 - > 1 - > 3 - > 5 - >3 - > 6 - > 3 - > 1 - > 4 - > 7 - > 9 - > 7 - > 4 - > 1 - > 0 - > 2 - > 8 - >9;
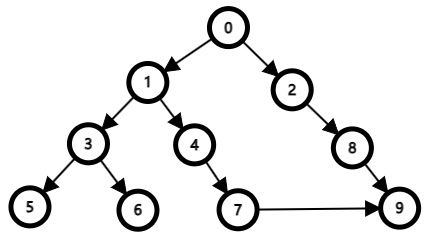
可以看到遍历方法优先增加深度（即 层数）
即能向下一层移动，就先向下一层移动，若没有，则回溯到上一层
形象点说是 《长驱直入》，也可以说是一条路走到黑（再回头）；
典型的递归（不是吗）
DFS模版
int dfs(int k) //k为递归层数，或要填第几个空
{
if(满足输出条件，或空全被填完) //即递归出口
{
输出解; //若有特殊输出格式，用自定义的 void print 函数
}
else
{
for(int i=1;i<=尝试方法数;i++)
if(满足进一步搜索条件（合法）)
{
为进一步搜索所需要的状态打上标记（保存现场）;
dfs(k+1);
恢复到打标记前的状态（恢复现场）; //也就是说的{回溯一步}
}
}
}
此上为DFS的模版（一般的）可以看出主要依靠不断回溯来找到问题的解；
注意事项：
-
第一个
if是符合输出解的条件，第二个if是符合进一步搜索的条件； -
下一步搜索时，不是使用
return dfs(k+1)而是直接dfs(k+1)（可能会注意不到这个关键的地方，以至于每次写完不知道为什么只得到一个答案就返回主程序了）
-
for循环之后的if可以是多个; -
for循环边界
例题
- 排列型枚举：P1706 全排列问题
- 组合型枚举：P1157 组合的输出
一种为说排列型：
题意：
按照字典序输出自然数 1 到 n 所有不重复的排列；
可以看出输出解的条件为当前已选的数的个数为n时，打印解（用print函数）;
否则继续搜索；
代码如下：
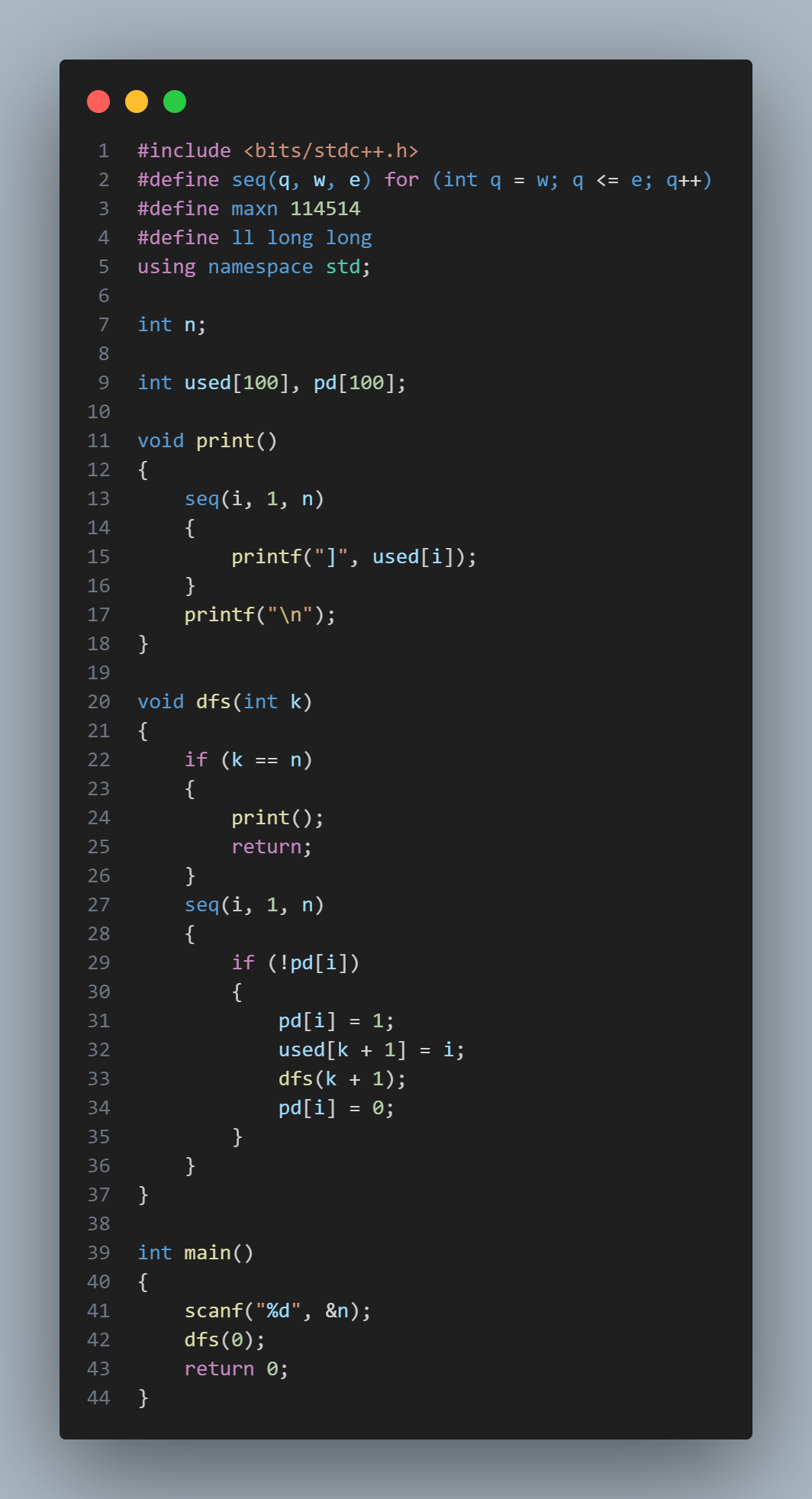
此题还有另外一种解法；（即全排列函数）
此为主角:
next_permutation
这个函数每运行一次就可以排列出下一个全排列的序列；
用法即是 next_permutation(数组开头，数组结尾)；
在此列一个例题：P1088 火星人
全排列问题的杀手锏；
另一种为组合型
题意：
从\(n\)个元素中选\(r\)个，共有多少种组合
思路：
由于是组合，所以与排列不同，组合不考虑元素的顺序
顺序：依次枚举每个位置放哪个数
具体代码：
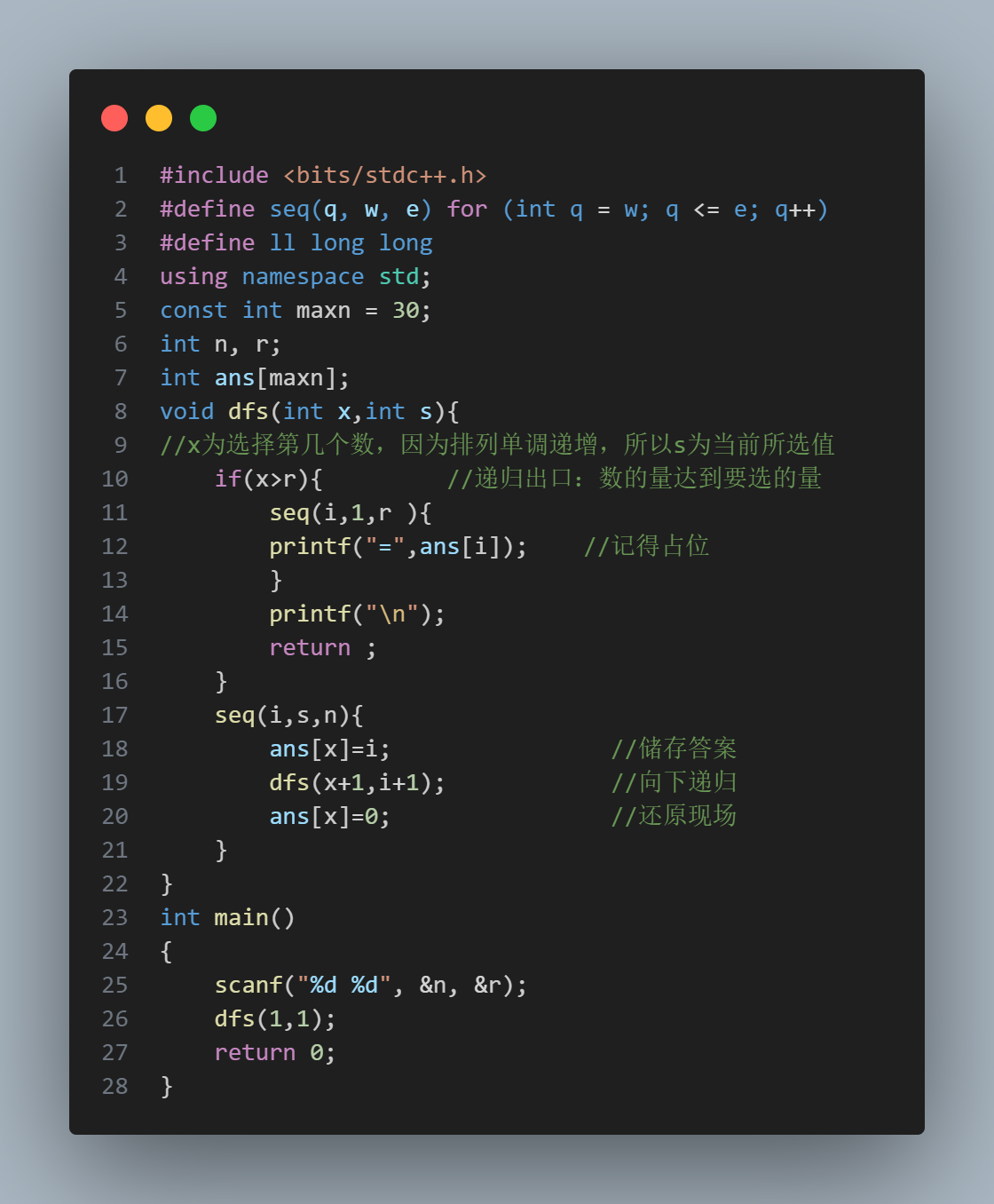
后记
不过这种方法也有不足之处
也用此图解释，若解为 \(2\) 时（或解答树比较稀疏时），这时遍历全部的树节点是完全没有必要的；
当然我们也有解决的办法（即广度优先搜索（BFS））
这也就显现出了DFS与BFS的不同和各自的适用范围
