算法心得
算法心得
选择排序与冒泡排序之间的关系
这几天学习算法,发现了一个有意思的现象。选择排序与冒泡排序的时间复杂度都是O(n^2)
并且呢,冒泡排序是两两相邻的去比较。而选择排序是一次比较所有。
/**
* 功能描述: 选择排序算法 --> int[] 是引用传递,即使不return input的指也会改变
* @Param: [input]
* @Return: int[]
* @Author: ADROITWOLF
* @Date: 2021/2/27 21:33
*/
public static int[] selectSort(int [] input){
int min = 0;
for (int i =0;i<input.length;i++ ){
min = i;
for(int j = i+1;j<input.length;j++){
min = input[min] > input[j] ? j:min;
}
if(i != min){ //说明最小值已经是那啥了
int tmp = input[i];
input[i] = input[min];
input[min] = tmp;
}
}
return input;
}
/**
* 功能描述: 冒泡排序
* @Param: [input]
* @Return: int[]
* @Author: ADROITWOLF
* @Date: 2021/2/27 21:56
*/
public static int[] bubbleSort(int [] input){
for (int i=0;i<input.length;i++){
for(int j=0;j<input.length-1;j++){
if(input[j] > input[j+1]){
int tmp = input[j];
input [j] = input[j+1];
input[j+1] = tmp;
}
}
}
return input;
}
为什么HashMap的时间复杂度可以为O(1)
通过《算法图解》这本书得知,散列表的查找时间复杂度是O(1)。具体实现方法是将输入数据和索引坐标做一个映射,并且散列表是通过数组来实现存储的,数组的查找时间复杂度为O(1)。HashMap的底层实现原理也是利用的散列表,所以他的时间复杂度为O(1).
并且,HashMap的使用极为广泛:
- 用作去重
- 作为缓存
- 映射查找遍历。
尾递归
尾递归说白了就是,在函数的后面直接return 自己,且没有任何的计算操作。举个例子:
public int recursion(int a){
if xxx{
return 1;
}else{
return recursion(a*x);
}
}
我们都知道递归会将函数压栈,不仅消耗大量的时间,而且有很大的不确定性,稳定性无法保证。 尾递归,则是编译器自动的将不重复调用栈,而是直接覆盖函数栈,使空间复杂度从O(n)变成了O(1)
递归和迭代的区别
首先这里一定要忘记迭代就是要比递归牛逼的想法,我记得我们老师说,尽量不要用递归,这纯属瞎扯淡误人子弟。
递归存在就有他的必要性,经过查阅发现,递归在用编译语言编写的时候更加的方便。对,就是方便!这是递归的非常大的优势。
并且只要能递归,就一定能转化成迭代,无非就是压栈的操作让我们手动模拟了而已。
求子集算法(回溯)
此题是leetcode 1886。
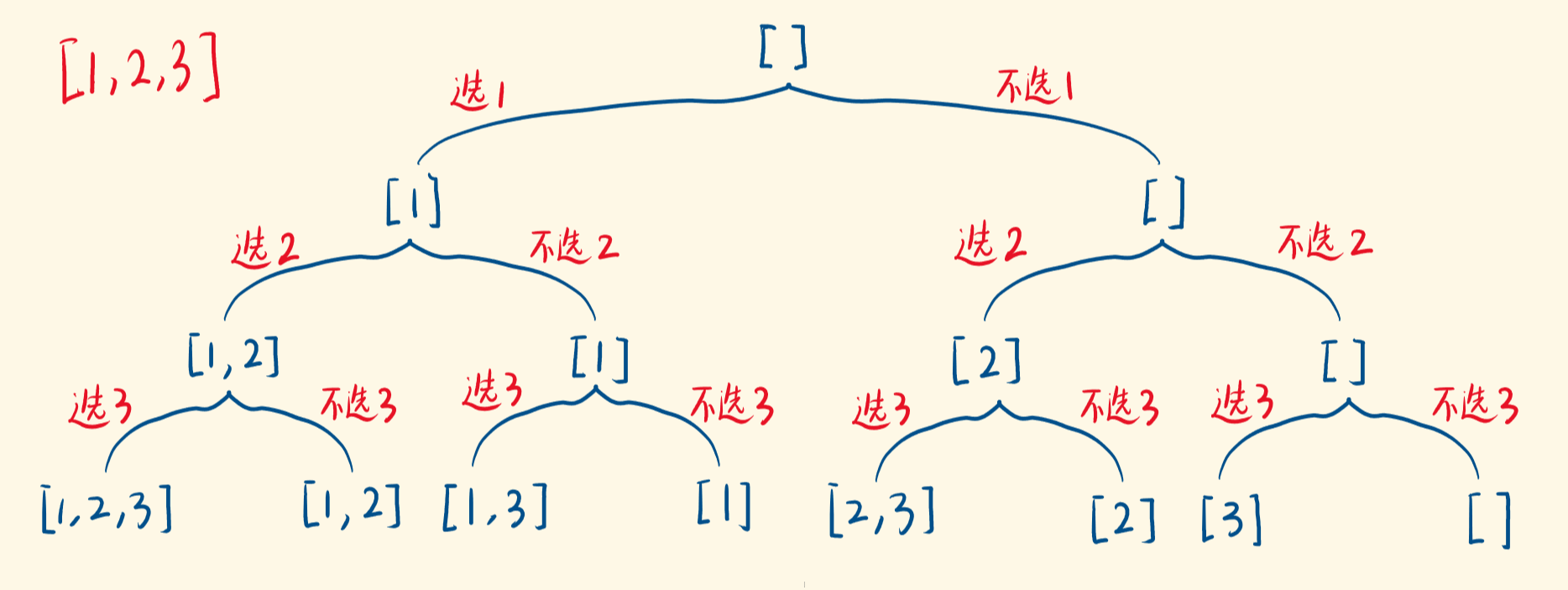
该题说白了,就是需要弄出一个决策树来,就像下面这样:
我们在遍历每个元素的时候都会面临着选和不选两个选项,这样我们就可以把子集就可以全部求出来了,具体代码如下(伪代码):
private int[][] res = new int [nums.length][nums.length];
public dfs(int [] nums,int index,int [] temp){
if(index == nums.length){
// 把当前的集合添加到结果中
res.add(temp);
}
dfs(nums,index+1,temp.add(nums[index])); // 选择当前元素
dfs(nums,index+1,temp); // 不选择当前元素
}
c语言入参和形参
在学习861的时候,偶然翻出自己之前的代码,c语言这方面我现在完全不懂了,需要重新开始学,这里就遇到了一个入参和形参的问题。 记得没错的话,当入参传入的是值的话,入参的改变和形参是毫无关系的,但是当入参传入一个地址的时候,并且修改当前入参地址的里面的值的时候,形参会随之改变。
当我们传入数组p的时候,我们其实传入的是p的首地址,也就是&p[0]。后面动态修改数组也是默认*p,所以形参数组也会跟着改变。
top K 问题
topk 一般使用顶堆去解决