有关求学习强连通的心得!
现在学了求强连通的两个算法(Tarjan算法和Kosaraju算法);其实还有其他一个算法的!没学所以就不写上来了!
Tarjan算法:
这个算法是在一次的dfs遍历的情况下完成的!每个节点都只有一次的访问的机会!我们在这个算法要用到栈!每碰到未访问的节点就进栈!如果不符合上述的条件就退栈!(怎么那么像走迷宫的?其实不是啊!相似而已,莫激动)!在这里我们用到low[n],dfs[n],这两个数组!dfs(u)为节点u搜索的次序编号(时间戳),low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。
算法伪代码如下
tarjan(u)
{
DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值
Stack.push(u) // 将节点u压入栈中
for each (u, v) in E // 枚举每一条边
if (v is not visted) // 如果节点v未被访问过
tarjan(v) // 继续向下找
Low[u] = min(Low[u], Low[v])
else if (v in S) // 如果节点v还在栈内
Low[u] = min(Low[u], DFN[v])
if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
repeat
v = S.pop // 将v退栈,为该强连通分量中一个顶点
print v
until (u== v)
}
接下来是对算法流程的演示。
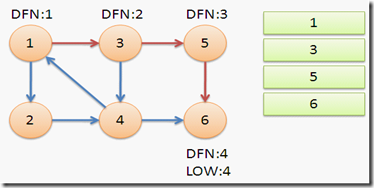
从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。
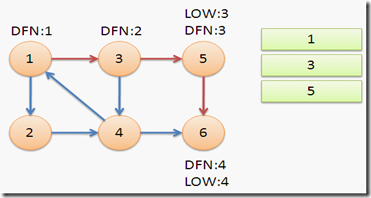
返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
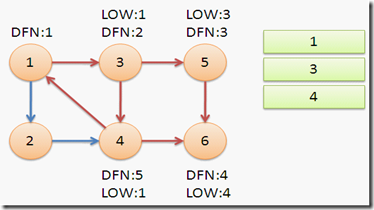
返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。
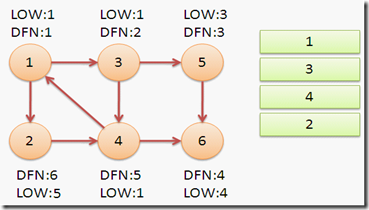
继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
至此,算法结束。经过该算法,求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
Kosaraju算法:
这个算法是基于两次的dfs操作的!操作大概如下:
1:dfs图并记录节点的访问时间:
2:根据记录的节点的访问时间降序遍历反向图,得到的每个连通块就是一个强连通分量:
Kosaraju算法的显著特征是,第一,引用了有向图的逆图;第二,需要对图进行两次DFS(一次在逆图上,一次在原图上)。而且这个算法依赖于一个事实:一个有向图的强连通分量与其逆图是一样的(即假如顶点任意顶点s与t属于原图中的一个强连通分量,那么在逆图中这两个顶点必定也属于同一个强连通分量,这个事实由强连通性的定义可证)。由于算法的时间取决于两次DFS,因此时间复杂度,对于稀疏图是O(V+E),对于稠密图是O(V²),可见这是一个线性算法。Kosaraju的结论是,在第二次DFS中,同一棵搜索树上的结点属于一个强连通分量。
下面我们来举例::

第1 步:对于有向图G 一次DFS 遍历得到的森林:
有上面可得到如下结论:
●在每个生成树中,根的时间戳最大;
●根可以到达该树的任何一个结点(其他结点不一定能到达根);
●每棵子树的根的时间戳都大于其后代结点;他也可以到达它的所有
后代;
第2 步:现在我们对图进行反向,然后按时间戳由大到小进行dfs
得到森林如下:

通俗讲,这个原理就是:第一次dfs 的生成树中若存在回边,那么
边反方向后仍然可以相互到达,于是就是一个连通分量。这一点需要细
细体会。
另此算法
可将DFS换为BFS
不过在第一步中每次BFS要反序
在此题中
第一步
DFS为
3 5 2 4 1 7 6
BFS为
5 3 4 2 1 7 6
第2步
DFS为
6
7
1 4 5 2
3
BFS为
6
7
1 5 2 4
3
说真的我个人认为DFS的时间比BFS慢!没验证!
这是我的一些心得,可能会不正确!请指出和原谅啊!