发表于 2016-05-28 | 分类于 CNN ， Op | 阅读次数： 16077

在训练深层神经网络的过程中, 由于输入层的参数在不停的变化, 因此, 导致了当前层的分布在不停的变化, 这就导致了在训练的过程中, 要求 learning rate 要设置的非常小, 另外, 对参数的初始化的要求也很高. 作者把这种现象称为 internal convariate shift. Batch Normalization 的提出就是为了解决这个问题的. BN 在每一个 training mini-batch 中对每一个 feature 进行 normalize. 通过这种方法, 使得网络可以使用较大的 learning rate, 而且, BN 具有一定的 regularization 作用.

为什么需要 Batch Normalization

在神经网络的优化中最常用最进本的方法是 SGD, 其目标是寻找最小化 loss function 的参数:

minibatch 计算出来的 loss 可以看做是整个 trainset 的 loss 的近似值.
minibatch 中, 可以并行地计算 m 各样本, 因此, 使用 minibatch 的方法比原始的 SGD 方法速度更快.

然而, SGD 算法有其固有缺点:

对初始值要求很高, 如果参数的初始化不好, 经常不能收敛
学习率比较难设置, 由于每一层 input 数据的 scale 不同, 导致 backward 的梯度的 scale 也不同, 为了保证不会 gradient vanish, 只能设置较小的 learning rate, 而, 较小的 learning rate 使得整个学习过程很慢
第 N 层的输入受前面 N-1 层的影响, 在深度学习中, 网络层数很多, 因此, 及时前面 layer 的很小的影响, 当到达第 N 层的时候, 会被放大很多倍.

在深度神经网络中, 每一层输入数据的分布都不同, 因此, 每一层的参数都要去学习不同的分布. 而主要由于上述 #3 的原因, 使得这个过程比较困难. 为了说明这个问题, 使用一个简单的例子. 考虑如下的一个两层的神经网络:

Batch Normalization 是什么

Input: Values of

为什么 Batch Normalization 可以加速训练

允许网络使用较高的 learning rate. 在传统的深度网络训练中, 如果使用较大的 learning rate 很容易导致 gradient vanish 或者 gradient explode. 通过在整个网络中 normalize activations, 可以防止参数的较小的改变被应用到较大的或者次优的 activation 中. 另一方面, BN 使得网络对于 parameter 的 scale 更加鲁棒. 通常情况下, large learning rate 会 increase the scale of layer parameters, 进而会放大 BP 的梯度, 导致了 model explosion. BN 的使用使得网络在 BP 的时候不会受到 parameter scale 的影响. 这是因为:
具有一定的 regularization 作用, 可以减少 Dropout 的使用. dropout 的作用是方法 overfitting, 实验发现, BN 可以 reduce overfitting.
降低
取消 LRN(Local Response Normalization).
Reduce the photomatric distortions. 因为 BN 使得训练过程更快, 能 observe 到的 sample 次数变少, 所以, 减少 distorting 使得网络 focus 在真实的图片上面.
BN 不仅仅限定在 ReLU 上, 而且, 对其它的 activation 也同样适用.

基础 | batchnorm原理及代码详解

前言：Batchnorm是深度网络中经常用到的加速神经网络训练，加速收敛速度及稳定性的算法，可以说是目前深度网络必不可少的一部分。
本文旨在用通俗易懂的语言，对深度学习的常用算法–batchnorm的原理及其代码实现做一个详细的解读。本文主要包括以下几个部分。

Batchnorm主要解决的问题
Batchnorm原理解读
Batchnorm的优点
Batchnorm的源码解读

第一节：Batchnorm主要解决的问题

首先，此部分也即是讲为什么深度网络会需要 $b a t c h n o r m$

1.1 Internal Covariate Shift

$I n t e r n a l$

$B a t c h$

1.2 covariate shift

$I n t e r n a l$

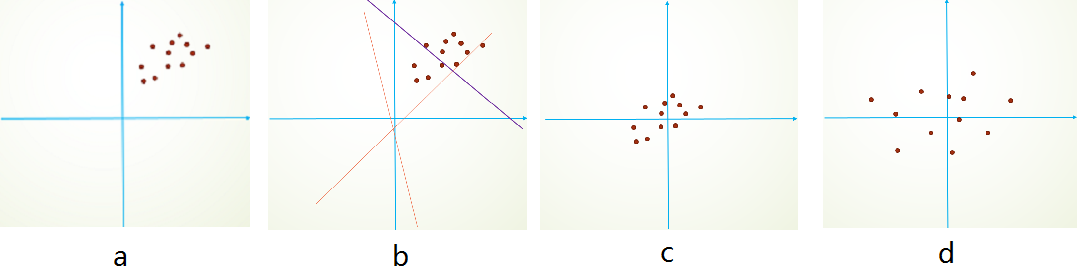
图片来自网络

举个简单线性分类栗子，假设我们的数据分布如a所示，参数初始化一般是0均值，和较小的方差，此时拟合的 $y = w x + b$

$C o v a r i a t e$

第二节：Batchnorm 原理解读

本部分主要结合原论文部分，排除一些复杂的数学公式，对 $B a t c h N o r m$

之前就说过，为了减小 $I n t e r n a l$

之所以称之为batchnorm是因为所norm的数据是一个batch的，假设输入数据是 $β = x_{1... m}$

1.先求出此次批量数据 $x$

接下来详细介绍一下这额外的两个参数，之前也说过如果直接做归一化不做其他处理，神经网络是学不到任何东西的，但是加入这两个参数后，事情就不一样了，先考虑特殊情况下，如果 $γ$

先用一个简单的代码举个小栗子：

def Batchnorm_simple_for_train(x, gamma, beta, bn_param):
"""
param:x    : 输入数据，设shape(B,L)
param:gama : 缩放因子  γ
param:beta : 平移因子  β
param:bn_param   : batchnorm所需要的一些参数
    eps      : 接近0的数，防止分母出现0
    momentum : 动量参数，一般为0.9， 0.99， 0.999
    running_mean ：滑动平均的方式计算新的均值，训练时计算，为测试数据做准备
    running_var  : 滑动平均的方式计算新的方差，训练时计算，为测试数据做准备
"""
    running_mean = bn_param['running_mean']  #shape = [B]
    running_var = bn_param['running_var']    #shape = [B]
    results = 0. # 建立一个新的变量

    x_mean=x.mean(axis=0)  # 计算x的均值
    x_var=x.var(axis=0)    # 计算方差
    x_normalized=(x-x_mean)/np.sqrt(x_var+eps)       # 归一化
    results = gamma * x_normalized + beta            # 缩放平移

    running_mean = momentum * running_mean + (1 - momentum) * x_mean
    running_var = momentum * running_var + (1 - momentum) * x_var

    #记录新的值
    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var 

    return results , bn_param

看完这个代码是不是对batchnorm有了一个清晰的理解，首先计算均值和方差，然后归一化，然后缩放和平移，完事！但是这是在训练中完成的任务，每次训练给一个批量，然后计算批量的均值方差，但是在测试的时候可不是这样，测试的时候每次只输入一张图片，这怎么计算批量的均值和方差，于是，就有了代码中下面两行，在训练的时候实现计算好 $m e a n$

running_mean = momentum * running_mean + (1 - momentum) * x_mean
running_var = momentum * running_var + (1 - momentum) * x_var

所以，测试的时候是这样的：

def Batchnorm_simple_for_test(x, gamma, beta, bn_param):
"""
param:x    : 输入数据，设shape(B,L)
param:gama : 缩放因子  γ
param:beta : 平移因子  β
param:bn_param   : batchnorm所需要的一些参数
    eps      : 接近0的数，防止分母出现0
    momentum : 动量参数，一般为0.9， 0.99， 0.999
    running_mean ：滑动平均的方式计算新的均值，训练时计算，为测试数据做准备
    running_var  : 滑动平均的方式计算新的方差，训练时计算，为测试数据做准备
"""
    running_mean = bn_param['running_mean']  #shape = [B]
    running_var = bn_param['running_var']    #shape = [B]
    results = 0. # 建立一个新的变量

    x_normalized=(x-running_mean )/np.sqrt(running_var +eps)       # 归一化
    results = gamma * x_normalized + beta            # 缩放平移

    return results , bn_param

你是否理解了呢？如果还没有理解的话，欢迎再多看几遍。

第三节：Batchnorm源码解读

本节主要讲解一段tensorflow中 $B a t c h n o r m$

def batch_norm_layer(x, train_phase, scope_bn):
    with tf.variable_scope(scope_bn):
        # 新建两个变量，平移、缩放因子
        beta = tf.Variable(tf.constant(0.0, shape=[x.shape[-1]]), name='beta', trainable=True)
        gamma = tf.Variable(tf.constant(1.0, shape=[x.shape[-1]]), name='gamma', trainable=True)

        # 计算此次批量的均值和方差
        axises = np.arange(len(x.shape) - 1)
        batch_mean, batch_var = tf.nn.moments(x, axises, name='moments')

        # 滑动平均做衰减
        ema = tf.train.ExponentialMovingAverage(decay=0.5)

        def mean_var_with_update():
            ema_apply_op = ema.apply([batch_mean, batch_var])
            with tf.control_dependencies([ema_apply_op]):
                return tf.identity(batch_mean), tf.identity(batch_var)
        # train_phase 训练还是测试的flag
        # 训练阶段计算runing_mean和runing_var，使用mean_var_with_update（）函数
        # 测试的时候直接把之前计算的拿去用 ema.average(batch_mean)
        mean, var = tf.cond(train_phase, mean_var_with_update,
                            lambda: (ema.average(batch_mean), ema.average(batch_var)))
        normed = tf.nn.batch_normalization(x, mean, var, beta, gamma, 1e-3)
    return normed

至于此行代码tf.nn.batch_normalization（）就是简单的计算batchnorm过程啦，代码如下：
这个函数所实现的功能就如此公式： $\frac{γ (x - μ)}{σ} + β$

def batch_normalization(x,
                        mean,
                        variance,
                        offset,
                        scale,
                        variance_epsilon,
                        name=None):

    with ops.name_scope(name, "batchnorm", [x, mean, variance, scale, offset]):
        inv = math_ops.rsqrt(variance + variance_epsilon)
        if scale is not None:
            inv *= scale
        return x * inv + (offset - mean * inv
                      if offset is not None else -mean * inv)

第四节：Batchnorm的优点

主要部分说完了，接下来对BatchNorm做一个总结：

没有它之前，需要小心的调整学习率和权重初始化，但是有了BN可以放心的使用大学习率，但是使用了BN，就不用小心的调参了，较大的学习率极大的提高了学习速度，
Batchnorm本身上也是一种正则的方式，可以代替其他正则方式如dropout等
另外，个人认为，batchnorm降低了数据之间的绝对差异，有一个去相关的性质，更多的考虑相对差异性，因此在分类任务上具有更好的效果。

注：或许大家都知道了，韩国团队在2017NTIRE图像超分辨率中取得了top1的成绩，主要原因竟是去掉了网络中的batchnorm层，由此可见，BN并不是适用于所有任务的，在image-to-image这样的任务中，尤其是超分辨率上，图像的绝对差异显得尤为重要，所以batchnorm的scale并不适合。

参考文献：
【1】http://blog.csdn.net/zhikangfu/article/details/53391840
【2】http://geek.csdn.net/news/detail/160906
【3】 https://www.zhihu.com/question/53133249

http://shuokay.com/2016/05/28/batch-norm/

Notes on Batch Normalization

发表于 2016-05-28 | 分类于 CNN ， Op | 阅读次数： 16072

为什么需要 Batch Normalization

在神经网络的优化中最常用最进本的方法是 SGD, 其目标是寻找最小化 loss function 的参数:

θ = a r g m i n θ 1 N \sum i = 1 N L ( x i , θ )

在求解的过程中, 一般是使用 minibatch 的方法, 简单来说, 就是计算下面的梯度:

1 m \sum \partial L ( x i , θ ) \partial θ

使用 minibatch 的方法有两个好处:

minibatch 计算出来的 loss 可以看做是整个 trainset 的 loss 的近似值.
minibatch 中, 可以并行地计算 m 各样本, 因此, 使用 minibatch 的方法比原始的 SGD 方法速度更快.

然而, SGD 算法有其固有缺点:

对初始值要求很高, 如果参数的初始化不好, 经常不能收敛
学习率比较难设置, 由于每一层 input 数据的 scale 不同, 导致 backward 的梯度的 scale 也不同, 为了保证不会 gradient vanish, 只能设置较小的 learning rate, 而, 较小的 learning rate 使得整个学习过程很慢
第 N 层的输入受前面 N-1 层的影响, 在深度学习中, 网络层数很多, 因此, 及时前面 layer 的很小的影响, 当到达第 N 层的时候, 会被放大很多倍.

F 2 (F 1 (θ 1, x), θ 2)

F_{1}

Batch Normalization 是什么

Input: Values of $x$

μ β σ 2 β x^i y i = 1 m \sum

为什么 Batch Normalization 可以加速训练

允许网络使用较高的 learning rate. 在传统的深度网络训练中, 如果使用较大的 learning rate 很容易导致 gradient vanish 或者 gradient explode. 通过在整个网络中 normalize activations, 可以防止参数的较小的改变被应用到较大的或者次优的 activation 中. 另一方面, BN 使得网络对于 parameter 的 scale 更加鲁棒. 通常情况下, large learning rate 会 increase the scale of layer parameters, 进而会放大 BP 的梯度, 导致了 model explosion. BN 的使用使得网络在 BP 的时候不会受到 parameter scale 的影响. 这是因为: $B N (W u) = B N ((a W) u) \partial B N ( ($
具有一定的 regularization 作用, 可以减少 Dropout 的使用. dropout 的作用是方法 overfitting, 实验发现, BN 可以 reduce overfitting.
降低 $L_{2}$
取消 LRN(Local Response Normalization).
Reduce the photomatric distortions. 因为 BN 使得训练过程更快, 能 observe 到的 sample 次数变少, 所以, 减少 distorting 使得网络 focus 在真实的图片上面.
BN 不仅仅限定在 ReLU 上, 而且, 对其它的 activation 也同样适用.

posted on 2018-06-06 16:36 Maddock 阅读(1898) 评论(0) 编辑收藏举报

刷新页面返回顶部

Image Process

基础 | batchnorm原理及代码详解

https://blog.csdn.net/qq_25737169/article/details/79048516

Notes on Batch Normalization

Notes on Batch Normalization

为什么需要 Batch Normalization

Batch Normalization 是什么

为什么 Batch Normalization 可以加速训练

基础 | batchnorm原理及代码详解

第一节：Batchnorm主要解决的问题

1.1 Internal Covariate Shift

1.2 covariate shift

第二节：Batchnorm 原理解读

第三节：Batchnorm源码解读

第四节：Batchnorm的优点

Notes on Batch Normalization

为什么需要 Batch Normalization

Batch Normalization 是什么

为什么 Batch Normalization 可以加速训练

导航

公告