机器学习之梯度提升决策树GBDT

集成学习总结

简单易学的机器学习算法——梯度提升决策树GBDT

 GBDT(Gradient Boosting Decision Tree)

Boosted Tree：一篇很有见识的文章

https://www.zhihu.com/question/54332085

AdaBoost与GBDT的区别

通俗来说不是很好说，我这里简单说说两者的相同点和不同点。相同点：模型都是加法模型、学习算法都是前向分布算法；每一步都需要训练一个弱分类器来弥补上一轮弱分类器的不足。不同点：Adaboost是新的弱学习器拟合不同权值或概率分布训练样本，而Gradient Boost是新的弱学习器拟合损失函数的负梯度在上一个模型的值。梯度提升树（回归树）的算法与原始的提升树（回归树）算法的核心区别主要在于残差计算这里，由于原始的回归树指定了平方损失函数所以可以直接计算残差，而梯度提升树针对一般损失函数，所以采用负梯度来近似求解残差。

作者：大器不早成
链接：https://www.zhihu.com/question/54332085/answer/281676652
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

 

梯度提升树(GBDT)原理小结

从回归树到GBDT

http://blog.csdn.net/zqxnum1/article/details/44337557

回归树

 

 

 

 

 

 

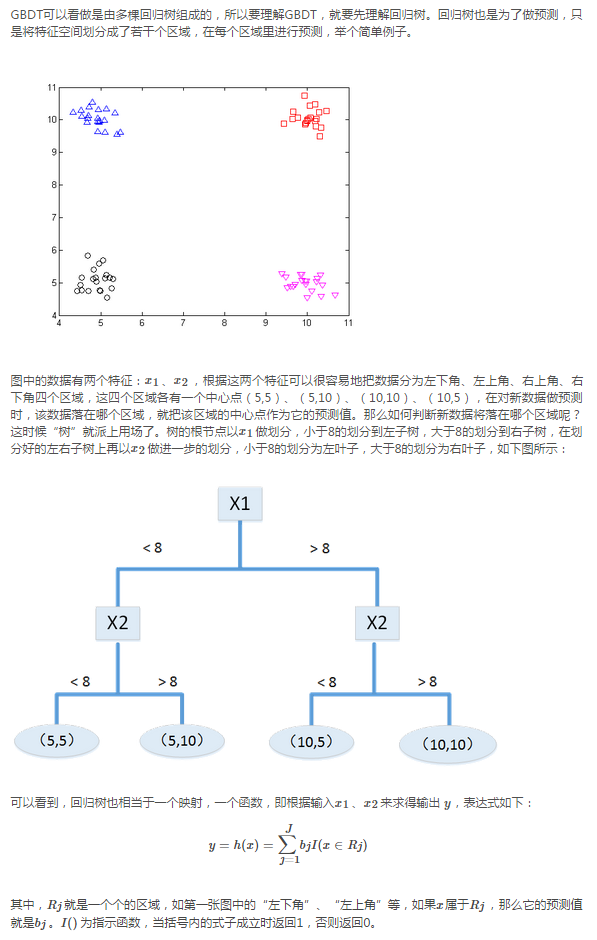
7、GBDT

 https://www.2cto.com/kf/201605/509184.html

此处，请仅关注GBDT的流程那个例子

 

 

一、DT：回归树RegressionDecisionTree

提起决策树（DT,DecisionTree)绝大部分人首先想到的就是C4.5分类决策树。但如果一开始就把GBDT中的树想成分类树，那就是一条歪路走到黑，一路各种坑，最终摔得都要咯血了还是一头雾水说的就是LZ自己啊有木有。咳嗯，所以说千万不要以为GBDT是很多棵分类树。决策树分为两大类，回归树和分类树。前者用于预测实数值，如明天的温度、用户的年龄、网页的相关程度；后者用于分类标签值，如晴天/阴天/雾/雨、用户性别、网页是否是垃圾页面。这里要强调的是，前者的结果加减是有意义的，如10岁+5岁-3岁=12岁，后者则无意义，如男+男+女=到底是男是女？GBDT的核心在于累加所有树的结果作为最终结果，就像前面对年龄的累加（-3是加负3），而分类树的结果显然是没办法累加的，所以GBDT中的树都是回归树，不是分类树，这点对理解GBDT相当重要（尽管GBDT调整后也可用于分类但不代表GBDT的树是分类树）。那么回归树是如何工作的呢？

 

下面我们以对人的性别判别/年龄预测为例来说明，每个instance都是一个我们已知性别/年龄的人，而feature则包括这个人上网的时长、上网的时段、网购所花的金额等。

 

作为对比，先说分类树，我们知道C4.5分类树在每次分枝时，是穷举每一个feature的每一个阈值，找到使得按照feature<=阈值，和feature>阈值分成的两个分枝的熵最大的feature和阈值（熵最大的概念可理解成尽可能每个分枝的男女比例都远离1:1），按照该标准分枝得到两个新节点，用同样方法继续分枝直到所有人都被分入性别唯一的叶子节点，或达到预设的终止条件，若最终叶子节点中的性别不唯一，则以多数人的性别作为该叶子节点的性别。

 

回归树总体流程也是类似，不过在每个节点（不一定是叶子节点）都会得一个预测值，以年龄为例，该预测值等于属于这个节点的所有人年龄的平均值。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是最大熵，而是最小化均方差--即（每个人的年龄-预测年龄）^2的总和/N，或者说是每个人的预测误差平方和除以N。这很好理解，被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最靠谱的分枝依据。分枝直到每个叶子节点上人的年龄都唯一（这太难了）或者达到预设的终止条件（如叶子个数上限），若最终叶子节点上人的年龄不唯一，则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。若还不明白可以Google"RegressionTree"，或阅读本文的第一篇论文中RegressionTree部分。

 

二、GB：梯度迭代GradientBoosting

好吧，我起了一个很大的标题，但事实上我并不想多讲GradientBoosting的原理，因为不明白原理并无碍于理解GBDT中的GradientBoosting。喜欢打破砂锅问到底的同学可以阅读这篇英文wikihttp://en.wikipedia.org/wiki/Gradient_boosted_trees

 

Boosting，迭代，即通过迭代多棵树来共同决策。这怎么实现呢？难道是每棵树独立训练一遍，比如A这个人，第一棵树认为是10岁，第二棵树认为是0岁，第三棵树认为是20岁，我们就取平均值10岁做最终结论？--当然不是！且不说这是投票方法并不是GBDT，只要训练集不变，独立训练三次的三棵树必定完全相同，这样做完全没有意义。之前说过，GBDT是把所有树的结论累加起来做最终结论的，所以可以想到每棵树的结论并不是年龄本身，而是年龄的一个累加量。GBDT的核心就在于，每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学。这就是GradientBoosting在GBDT中的意义，简单吧。

 

三、GBDT工作过程实例。

还是年龄预测，简单起见训练集只有4个人，A,B,C,D，他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生；C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练，会得到如下图1所示结果：

 

现在我们使用GBDT来做这件事，由于数据太少，我们限定叶子节点做多有两个，即每棵树都只有一个分枝，并且限定只学两棵树。我们会得到如下图2所示结果：

在第一棵树分枝和图1一样，由于A,B年龄较为相近，C,D年龄较为相近，他们被分为两拨，每拨用平均年龄作为预测值。此时计算残差（残差的意思就是：A的预测值+A的残差=A的实际值），所以A的残差就是16-15=1（注意，A的预测值是指前面所有树累加的和，这里前面只有一棵树所以直接是15，如果还有树则需要都累加起来作为A的预测值）。进而得到A,B,C,D的残差分别为-1,1，-1,1。然后我们拿残差替代A,B,C,D的原值，到第二棵树去学习，如果我们的预测值和它们的残差相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的，第二棵树只有两个值1和-1，直接分成两个节点。此时所有人的残差都是0，即每个人都得到了真实的预测值。

 

换句话说，现在A,B,C,D的预测值都和真实年龄一致了。Perfect!：

A:14岁高一学生，购物较少，经常问学长问题；预测年龄A=15–1=14

B:16岁高三学生；购物较少，经常被学弟问问题；预测年龄B=15+1=16

C:24岁应届毕业生；购物较多，经常问师兄问题；预测年龄C=25–1=24

D:26岁工作两年员工；购物较多，经常被师弟问问题；预测年龄D=25+1=26

 

那么哪里体现了Gradient呢？其实回到第一棵树结束时想一想，无论此时的costfunction是什么，是均方差还是均差，只要它以误差作为衡量标准，残差向量(-1,1,-1,1)都是它的全局最优方向，这就是Gradient。