最小生成树算法

正文
      所谓最小生成树，就是在一个具有N个顶点的带权连通图G中，如果存在某个子图G'，其包含了图G中的所有顶点和一部分边，且不形成回路，并且子图G'的各边权值之和最小，则称G'为图G的最小生成树。
      由定义我们可得知最小生成树的三个性质：
      • 最小生成树不能有回路。
      • 最小生成树可能是一个，也可能是多个。
      • 最小生成树边的个数等于顶点的个数减一。

本文将介绍两种最小生成树的算法，分别为克鲁斯卡尔算法(Kruskal Algorithm)和普利姆算法(Prim Algorithm)。

一、克鲁斯卡尔算法(Kruskal Algorithm)

克鲁斯卡尔算法的核心思想是：在带权连通图中，不断地在边集合中找到最小的边，如果该边满足得到最小生成树的条件，就将其构造，直到最后得到一颗最小生成树。

克鲁斯卡尔算法的执行步骤：
第一步：在带权连通图中，将边的权值排序；
第二步：判断是否需要选择这条边（此时图中的边已按权值从小到大排好序）。判断的依据是边的两个顶点是否已连通，如果连通则继续下一条；如果不连通，那么就选择使其连通。
第三步：循环第二步，直到图中所有的顶点都在同一个连通分量中，即得到最小生成树。

下面我用图示法来演示克鲁斯卡尔算法的工作流程，如下图：

 

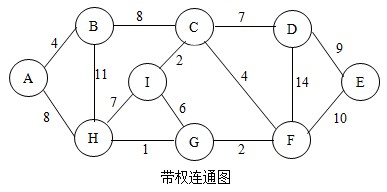
首先，将图中所有的边排序（从小到大），我们将以此结果来选择。排序后各边按权值从小到大依次是：

HG < (CI=GF) < (AB=CF) < GI < (CD=HI) < (AH=BC) < DE < BH < DF

接下来，我们先选择HG边，将这两个点加入到已找到点的集合。这样图就变成了，如图

 

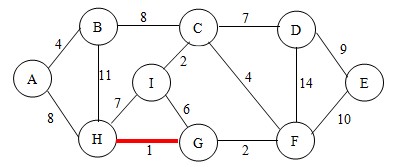
继续，这次选择边CI（当有两条边权值相等时，可随意选一条），此时需做判断。

判断法则：当将边CI加入到已找到边的集合中时，是否会形成回路？
     1.如果没有形成回路，那么直接将其连通。此时，对于边的集合又要做一次判断：这两个点是否在已找到点的集合中出现过？
          ①.如果两个点都没有出现过，那么将这两个点都加入已找到点的集合中；
          ②.如果其中一个点在集合中出现过，那么将另一个没有出现过的点加入到集合中；
          ③.如果这两个点都出现过，则不用加入到集合中。
     2.如果形成回路，不符合要求，直接进行下一次操作。

根据判断法则，不会形成回路，将点C和点I连通，并将点C和点I加入到集合中。如图：

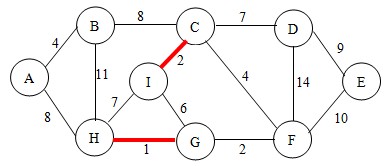
继续，这次选择边GF，根据判断法则，不会形成回路，将点G和点F连通，并将点F加入到集合中。如图：

继续，这次选择边AB，根据判断法则，不会形成回路，将其连通，并将点A和点B加入到集合中。如图：

继续，这次选择边CF，根据判断法则，不会形成回路，将其连通，此时这两个点已经在集合中了，所以不用加入。如图：

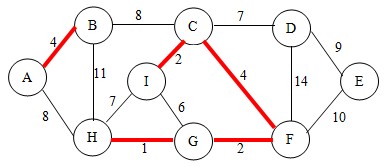
继续，这次选择边GI，根据判断法则，会形成回路，如下图，直接进行下一次操作：

 继续，这次选择边CD，根据判断法则，不会形成回路，将其连通，并将点D加入到集合中。如图：

继续，这次选择边HI，根据判断法则，会形成回路，直接进行下一次操作。
继续，这次选择边AH，根据判断法则，不会形成回路，将其连通，此时这两个点已经在集合中了，所以不用加入。
继续，这次选择边BC，根据判断法则，会形成回路，直接进行下一次操作。
继续，这次选择边DE，根据判断法则，不会形成回路，将其连通，并将点E加入到集合中。如图：

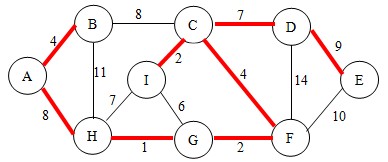
继续，这次选择边BH，根据法则，会形成回路，进行下一次操作。
最后选择边DF，根据法则，会形成回路，不将其连通，也不用加入到集合中。

好了，所有的边都遍历完成了，所有的顶点都在同一个连通分量中，我们得到了这颗最小生成树。

通过生成的过程可以看出，能否得到最小生成树的核心问题就是上面所描述的判断法则。
那么，我们如何用算法来描述判断法则呢？我认为只需要三个步骤即可：
    ⒈将某次操作选择的边XY的两个顶点X和Y和已找到点的集合作比较，如果
         ①这两个点都在已找到点的集合中，那么return 2；
         ②这两个点有一个在已找到点的集合中，那么return 1；
         ③这两个点都不在一找到点的集合中，那么return 0；
    ⒉当返回值为0或1时，可判定不会形成回路；
    ⒊当返回值为2时，判定能形成回路的依据是：假如能形成回路，设能形成回路的点的集合中有A,B,C,D四个点，那么以点A为起始点，绕环路一周后必能回到点A。如果能回到，则形成回路；如果不能，则不能形成回路。

#include<iostream>
#include<algorithm>
using namespace std;

const int size = 128; 
int n;
int father[size];
int rank[size];

//把每条边成为一个结构体，包括起点、终点和权值 
typedef struct node
{
    int val;
    int start;
    int end;    
}edge[SIZE * SIZE / 2];

//把每个元素初始化为一个集合 
void make_set()
{
    for(int i = 0; i < n; i ++){
        father[i] = i;
        rank[i] = 1;    
    }    
    return ;
}

//查找一个元素所在的集合,即找到祖先 
int find_set(int x)
{
    if(x != father[x]){
        father[x] = find_set(father[x]);    
    }    
    return father[x];
}

//合并x,y所在的两个集合：利用Find_Set找到其中两个
//集合的祖先，将一个集合的祖先指向另一个集合的祖先。
void Union(int x, int y)
{
    x = find_set(x);    
    y = find_set(y);
    if(x == y){
        return ;    
    }
    if(rank[x] < rank[y]){
        father[x] = find_set(y);    
    }
    else{
        if(rank[x] == rank[y]){
            rank[x] ++;    
        }    
        father[y] = find_set(x);
    }
    return ;
}

bool cmp(pnode a, pnode b)
{
    return a.val < b.val;    
}

int kruskal(int n) //n为边的数量 
{
    int sum = 0;
    make_set();
    for(int i = 0; i < n; i ++){   //从权最小的边开始加进图中 
        if(find_set(edge[i].start) != find_set(edge[i].end)){
            Union(edge[i].start, edge[i].end);
            sum += edge[i].val;    
        }    
    }
    return sum;    
}

int main()
{
    while(1){
        scanf("%d", &n);    
        if(n == 0){
            break;    
        }
        char x, y;
        int m, weight;
        int cnt = 0;
        for(int i = 0; i < n - 1; i ++){
            cin >> x >> m; 
            //scanf("%c %d", &x, &m);    
            //printf("%c %d ", x, m);
            for(int j = 0; j < m; j ++){
                cin >> y >> weight; 
                //scanf("%c %d", &y, &weight);
                //printf("%c %d ", y, weight);    
                edge[cnt].start = x - 'A';
                edge[cnt].end = y - 'A';
                edge[cnt].val = weight;
                cnt ++;
            }
        }
        
        sort(edge, edge + cnt, cmp); //对边按权从小到大排序 
        cout << kruskal(cnt) << endl; 
    }    
}

 

 二、普利姆算法(Prim Algorithm)

普利姆算法的核心步骤是：在带权连通图中，从图中某一顶点v开始，此时集合U={v}，重复执行下述操作：在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边，将(u,w)这条边加入到已找到边的集合，并且将点w加入到集合U中，当U=V时，就找到了这颗最小生成树。

其实，由步骤我们就可以定义查找法则：在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边。

ok，知道了普利姆算法的核心步骤，下面我就用图示法来演示一下工作流程，如图：

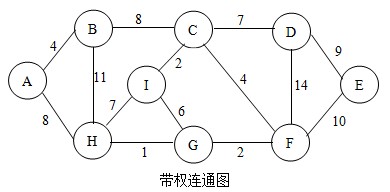
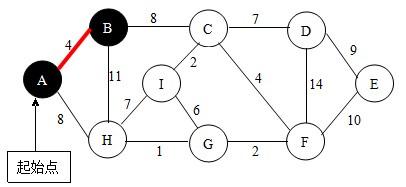
首先，确定起始顶点。我以顶点A作为起始点。根据查找法则，与点A相邻的点有点B和点H，比较AB与AH，我们选择点B，如下图。并将点B加入到U中。

继续下一步，此时集合U中有{A,B}两个点，再分别以这两点为起始点，根据查找法则，找到边BC（当有多条边权值相等时，可选任意一条），如下图。并将点C加入到U中。

继续，此时集合U中有{A,B,C}三个点，根据查找法则，我们找到了符合要求的边CI，如下图。并将点I加入到U中。

继续，此时集合U中有{A,B,C,I}四个点，根绝查找法则，找到符合要求的边CF，如下图。并将点F加入到集合U中。

继续，依照查找法则我们找到边FG,如下图。并将点G加入到U中。

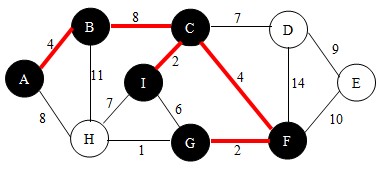
继续，依照查找法则我们找到边GH,如下图。并将点H加入到U中。

 

 继续，依照查找法则我们找到边CD,如下图。并将点D加入到U中。

 

 继续，依照查找法则我们找到边DE,如下图。并将点E加入到U中。

 

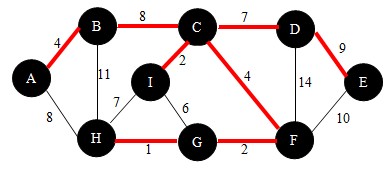
此时，满足U = V，即找到了这颗最小生成树。
附注：prim算法最小生成树的生成过程中，也有可能构成回路，需做判断。判断的方法和克鲁斯卡尔算法一样。

int prime(int cur)
{
    int index;
    int sum = 0;
    memset(visit, false, sizeof(visit));
    visit[cur] = true;
    for(int i = 0; i < m; i ++){
        dist[i] = graph[cur][i];    
    }
    
    for(int i = 1; i < m; i ++){
        
        int mincost = INF;
        for(int j = 0; j < m; j ++){
            if(!visit[j] && dist[j] < mincost){
                mincost = dist[j];
                index = j;    
            }    
        }
        
        visit[index] = true;
        sum += mincost;
        
        for(int j = 0; j < m; j ++){
            if(!visit[j] && dist[j] > graph[index][j]){
                dist[j] = graph[index][j];
            }    
        }    
    } 
    return sum;    
}

 

 

转载：http://blog.csdn.net/fengchaokobe/article/details/7521780
        http://www.cnblogs.com/aiyelinglong/archive/2012/03/26/2418707.html