本篇重点
1. 什么是堆,有什么特性?
2. 堆排序概述
3. 堆排序图解
4. 代码
5. 堆排序时间复杂度/空间复杂度/稳定性
6. 堆排序/堆适用场景
什么是堆
1. 堆是完全二叉树。一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的节点的位置相同,则这棵二叉树称为完全二叉树。
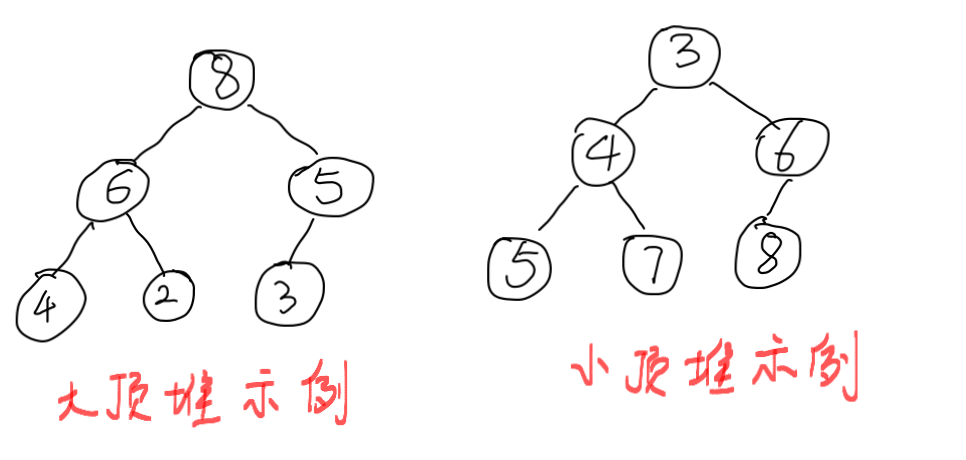
2. 堆分为大顶堆(大根堆)和小顶堆(小根堆)。 大顶堆中,每个父节点的数字都大于等于其左右子节点的数字;小顶堆中,每个父节点的数字都小于等于其左右子节点的数字。如下示例:
3. 为了更好的理解后面的算法,我们需要知道完全二叉树的特性:
1)叶子节点只可能在最后两层出现,且有空缺(叶子节点或只有一个叶子节点的父节点)的节点只能出现在右边。
2)完全二叉树的节点总数= (叶子节点数*2) or (叶子节点数*2-1) 如上图的示例中,叶子节点数为3, 总数为6. 如果”大顶堆示例“中的数字5有右边子节点的话,叶子节点数为4,节点总数7 = 4*2 -1.
3) 根据上面第二点我们反过来推,假设节点总数为n,叶子节点数为m, 那么n = (m*2) or (m*2 - 1) 。如果已知总节点数n,则m=n/2(n为偶数时),或者m=(n+1)/2(n为奇数时)。 一般在编程时,完全二叉树(我们这里的堆)是用数组表示,像上面说的, 对树的节点从上到下从左到右排列,根节点下标为0。我们假设第一个叶子节点的下标为i,那么i = n-m(因为第一个叶子节点后面都是叶子节点嘛)。则如下图:
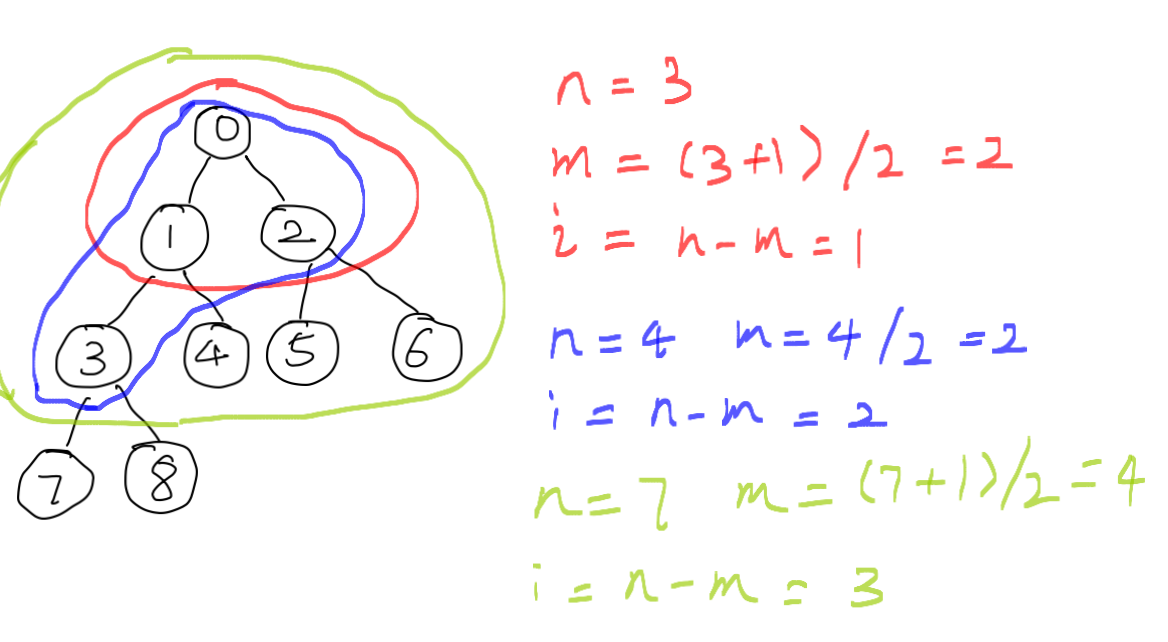
我们可以发现规律, 无论n为奇数或者偶数,i = n/2(向下取整)。 现在我们得到了第一个叶子节点的下标,最后一个非叶子节点就是它前面一个,下标为n/2-1
记住这最后一个非叶子节点的坐标,后面要用。
3) 已知节点下标为i,那么其父节点的下标为(i-1)/2(向下取整). 其左子节点下标为2*i+1, 右子节点下标为2*i+2
4) 已知节点总数为n,那么完全二叉树的高度为 log(n+1) 向上取整。推导:
这里说的高度是从根节点到叶子节点的最多节点数,也就是只有一个根节点的话高度是1, 2或者3个节点高度是2。。
我们知道完全二叉树的节点数是小于等于和它相同高度的满二叉树的节点数的,但是一定大于比它高度小1的的满二叉树的节点数的。 满二叉树的节点数与高度的公式为:n = 2^h-1, 其中h为高度。可以得到如下不等式:2^(h-1)-1 < n <= 2^h-1 , 两边同时加1再同时取以2为底的log得: h-1< log(n+1) <= h
堆排序概述
我们以进行升序排序为例:
1. 首先我们把待排序数组构建为一颗完全二叉树, 按照从上到下,从左到右的顺序安排节点。然后将其调整为大顶堆(如果是降序则是小顶堆,其他的一样),这时候根元素是最大的数字,将其和最后一个叶子节点,也就是数组中的最后一个位置交换。 这样最大的数字的位置就确定了。
2. 然后将除了最后一个数字的其他数字再次调整成大顶堆, 这时候根元素是全局第二大的数字,将其跟数组的倒数第二个元素交换。再将剩下的元素调整为大顶堆,以此来找到剩下元素中最大的,然后放到正确的位置。如此循环,直到所有的元素找到位置。
3. 所以此算法的重点在于如何将数组中的数字调整为大顶堆。调整的原则如下:
1)每次的调整都是三个节点为一个单位的:父节点,左子节点,右子节点。 如果左子节点或者右子节点比父节点大,那么从中选择最大的数字与父节点交换。
2)调整时是从最后一个非叶子节点(父节点)开始的,也就是我们上面推算出来的n/2-1的位置。方向是从下到上,从右到左。从最后一个父节点->倒数第二个父节点->...->根节点。下标的位置是依次递减。这是一个循环的过程。
3)调整时还有一个方向,如果在调整时发生了左子节点或者右子节点与根节点交换的情况。那么被交换的节点也是要进行一次调整,因为相当于我们把比较小的数字交换下来了,可能就不符合大顶堆的条件了。这是一个递归(也可以是循环)的过程。
4) 是上面的第2步,在初始建堆完成后,将待排序的最后一个数字和根节点交换,然后将除了最后一个数字的其他数字再次调整成大顶堆,这个步骤和后面循环的步骤中,由于只变化了根节点,其他的节点还保留着大顶堆的特性。所以不需要从最后一个父节点进行调整(因为它符合大顶堆特性),从根节点往下调整即可。
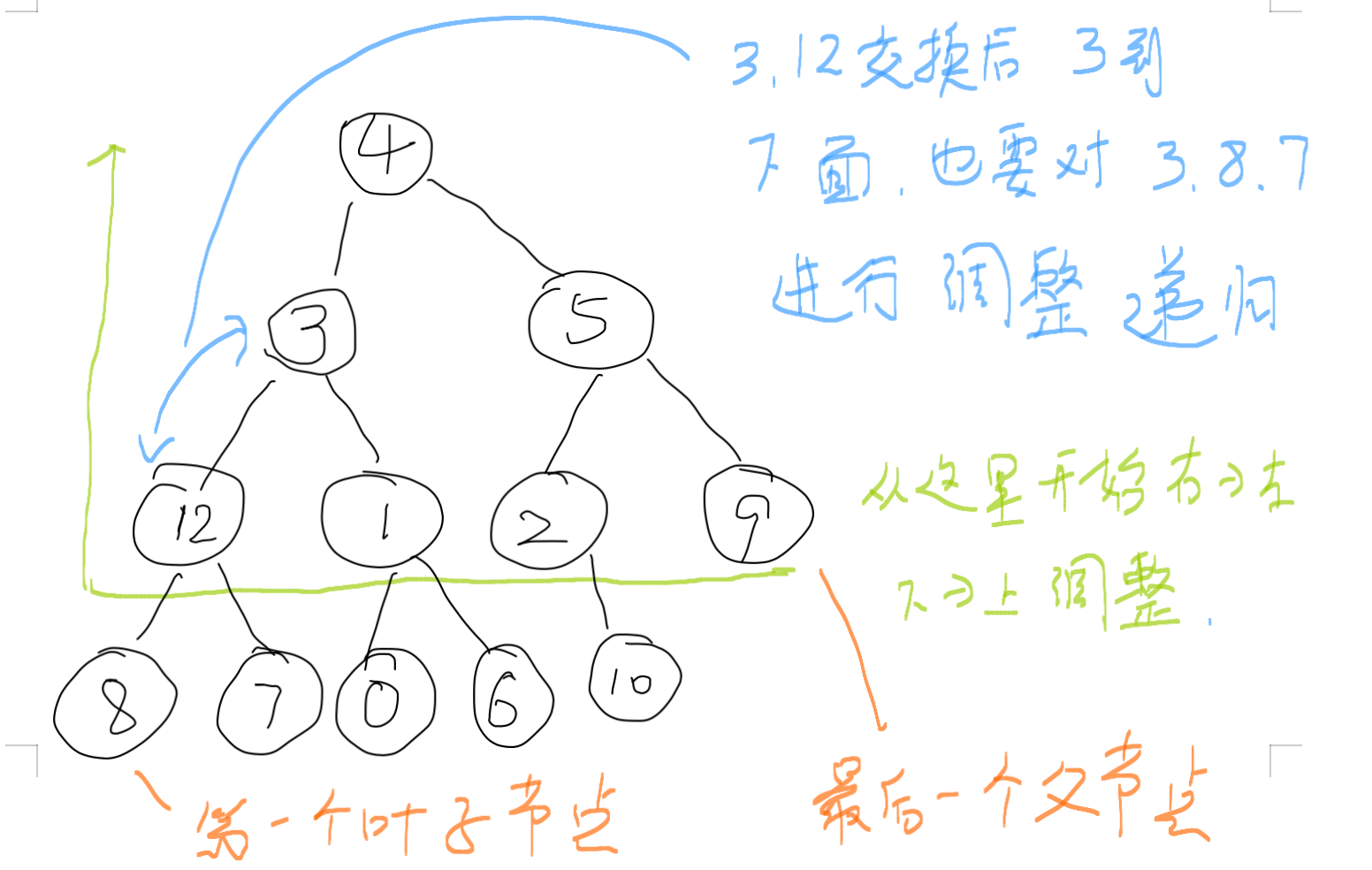
初始建堆时的调整顺序:
堆排序图解
我们仍然用上一篇手撕快速排序(含图解和两种实现代码含改进) 中的例子:
[4,3,8,1,-1,2,5,4] 初始完全二叉树如下图所示:
1. 从最后一个父节点开始调整,上面得出结论,最后一个父节点的坐标为n/2-1,这里n=8,所以是下标为3的节点,也就是数字1,它只有左子节点4,比它大,需要交换一下。交换后如右边所示,交换下来的1是叶子节点,没有必要继续调整。然后进入到进入到倒数第二个父节点,也就是下标为3的节点,也就是数字8,它比俩子节点都大,不用调整。 以下图中绿色的数字都表示在每次建堆的过程中,调整的节点的顺序。
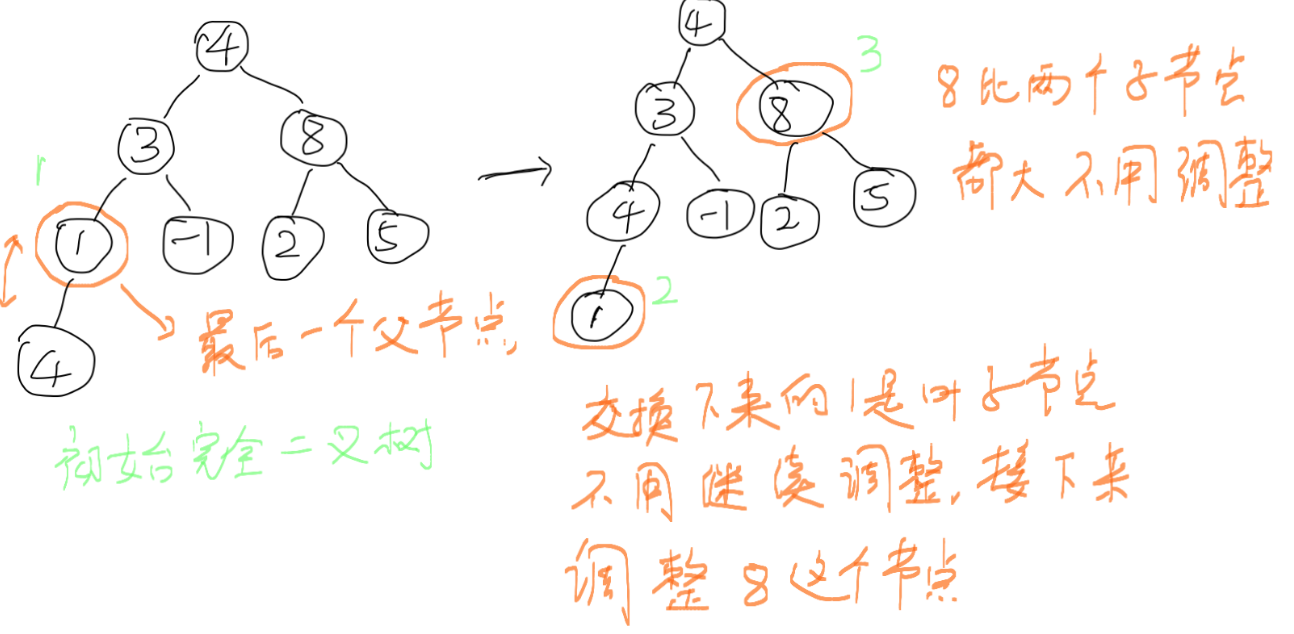
2. 下面调整下标为1的父节点,也就是数字3,需要跟左子节点4,交换一下。交换完成后如图中右侧所示,3比子节点1要大,不用交换,下面轮到调整下标为0的父节点,也就是根节点。
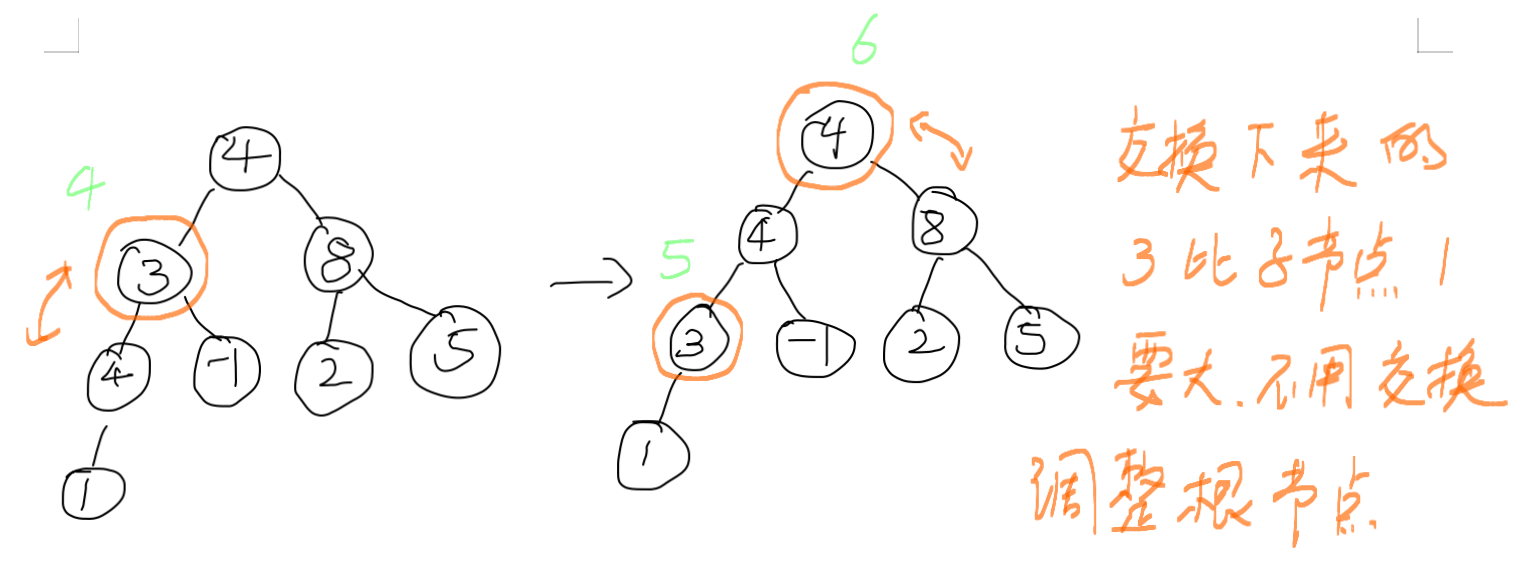
3. 根节点跟8交换。4交换下来之后,右子节点比它大,需要再调整一下。调整后完成了大顶堆。根元素最大
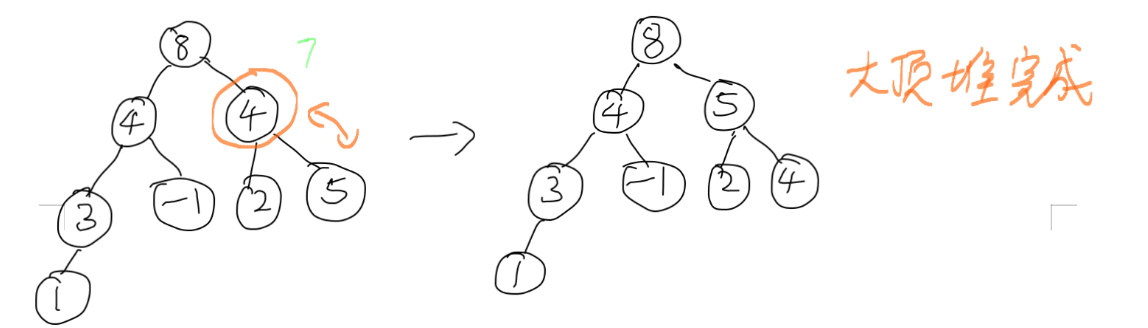
4. 把根元素跟最后的一个元素交换位置,最大元素的位置就确定了,可以排除在后面的操作之外了。然后把剩下的元素重新调整为大顶堆。 注意数字8虽然在图里,但是我用虚线表示,不参与到后面的操作中。这时候跟初始建堆的时候不一样,只有根节点的数字是从最后一个换上来的,其余的部分还是基本保持大顶推的特性的,所以从根节点开始调整即可。这里根节点1需要跟5交换一下。1交换下来之后还要跟4再交换一下。然后重新形成了大顶堆。
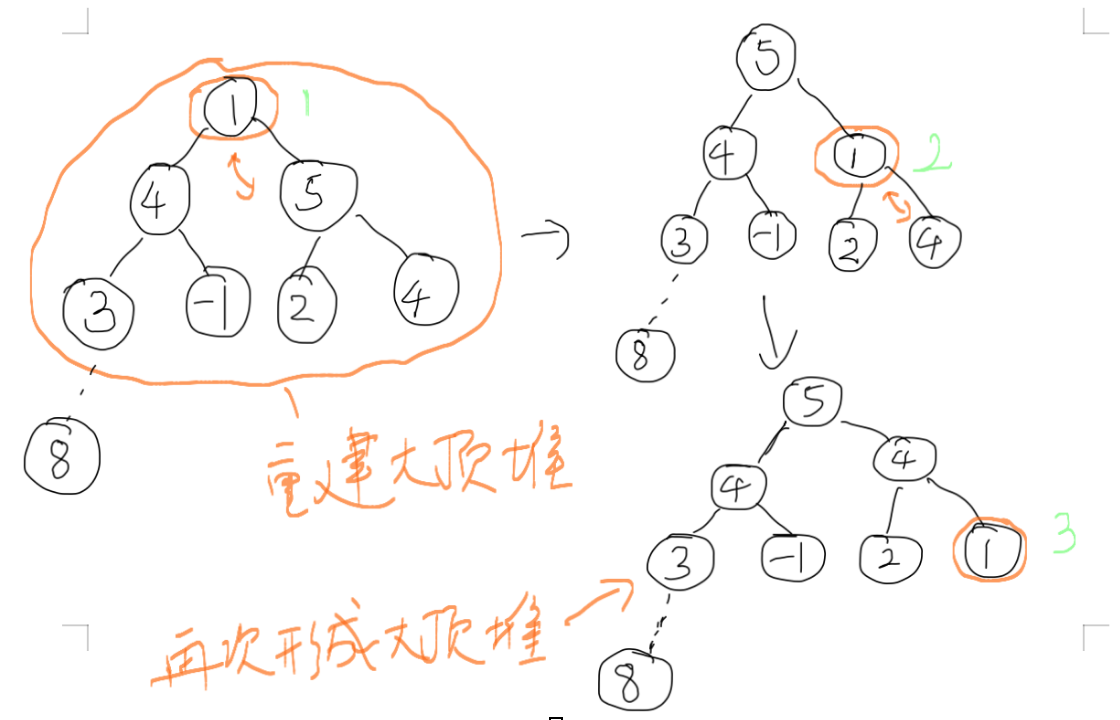
5. 这次的堆顶元素5是剩下的数字里面最大的,把它跟剩下的元素中的最后一个(全局的倒数第二个元素交换),然后把5也排除,剩下的重新调整为大顶堆。
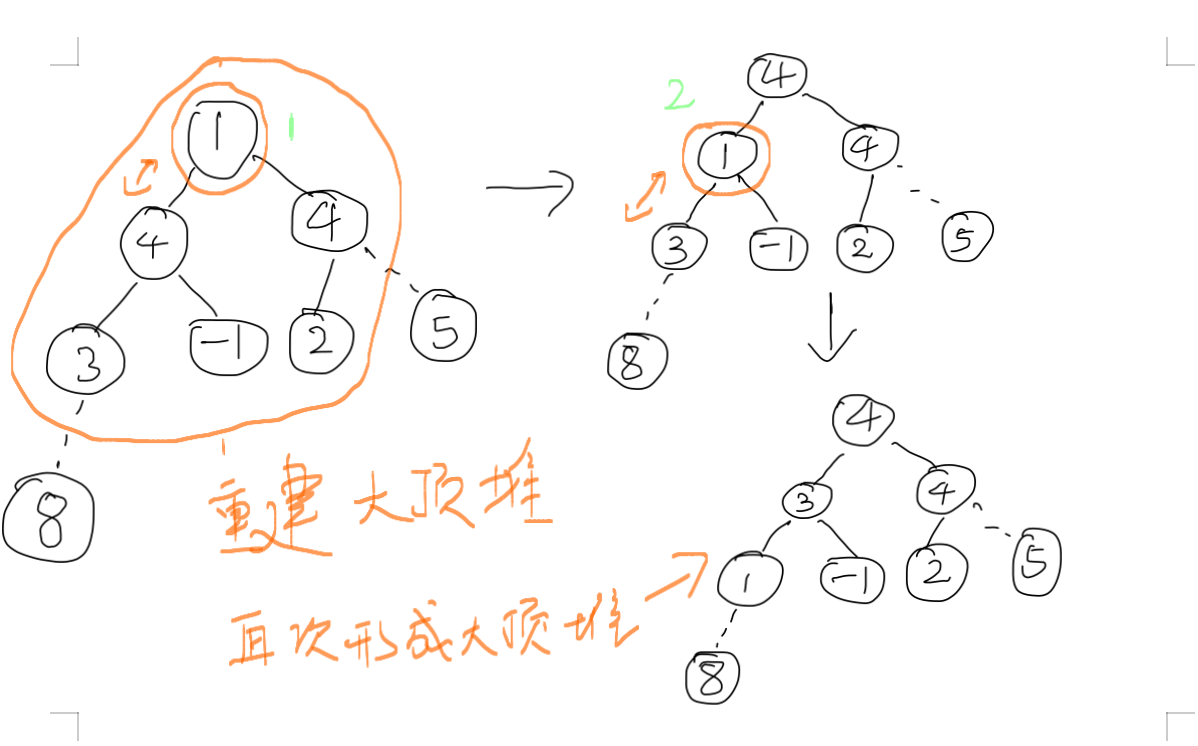
6.这次确定了4的位置,继续把剩下的元素调整,再把对顶元素跟剩下元素的最后一位交换,循环这种操作。
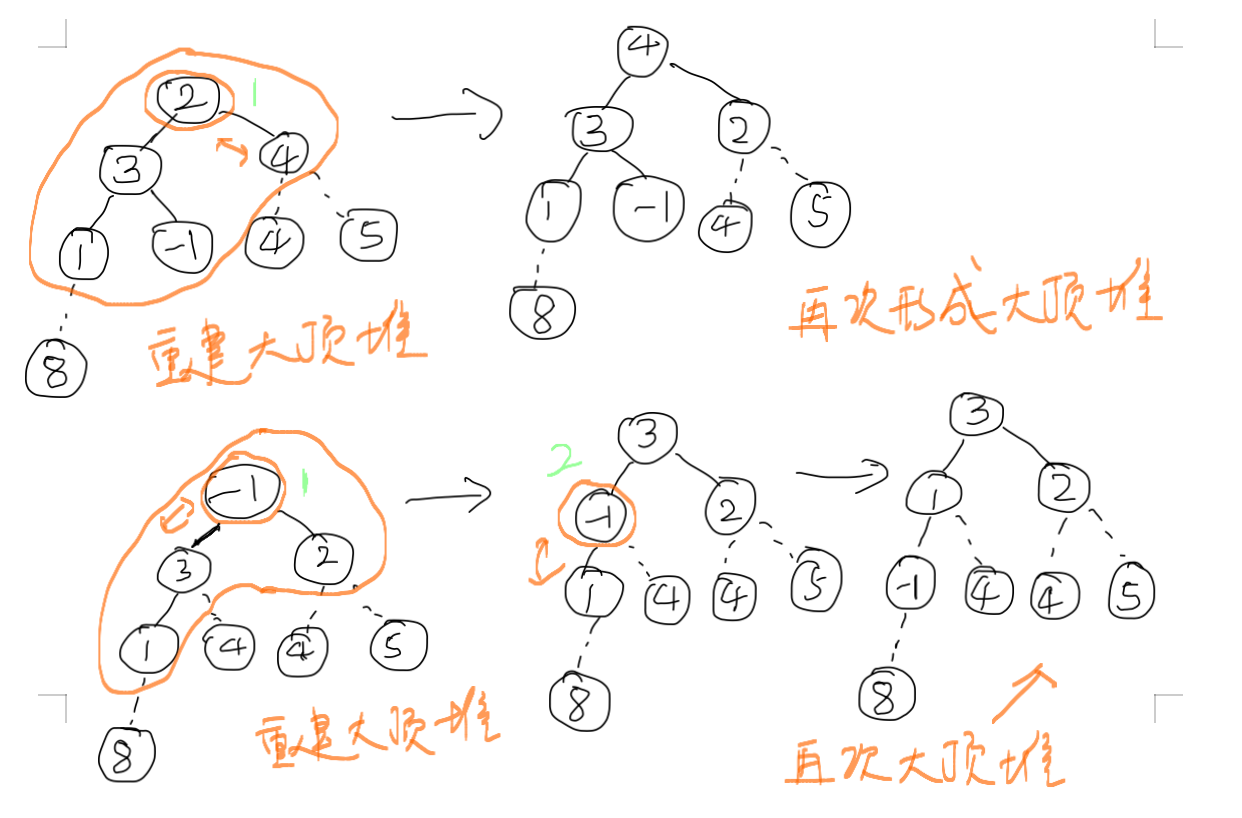
7. 图中我们展示了4,4,5,8几个元素都找到了位置,后面再重复如上的操作即可完成整个数组排序,此处不再赘述。
代码
private static void heapify(int[] tree, int n, int i) { //n 表示需要调整的节点总数 //i 表示要开始调整的节点下标 if(i>=n) {return;} int lefti = 2*i + 1; //左子节点下标 int righti = 2*i + 2; //右子节点下标 int maxi = i; if(lefti < n && tree[lefti] > tree[maxi]) { maxi = lefti; } if(righti < n && tree[righti] > tree[maxi]) { maxi = righti; } if(i != maxi) { swap(tree,i,maxi); heapify(tree,n,maxi); //如果发生了交换,则递归地对被交换下来的数字进行调整.最多次数为树的高度,O(logN)级别 } } private static void buildHeap(int[] tree,int n) { int lastNode = n/2-1; //初始建堆,从最后一个父节点开始调整 for (int i = lastNode; i >=0 ; i--) {//复杂度为O(N)级别 heapify(tree,n,i);//复杂度为O(logN)级别 } } public static void heapSort(int[] tree) { buildHeap(tree,tree.length); //O(N*logN) for (int i = tree.length-1; i >= 0; i--) { //O(N) swap(tree,0,i); //把根节点跟待排序数字中的最后一个进行交换。O(1) heapify(tree,i,0); //重新调整为大顶堆,这时从根节点开始调整即可. O(logN) } } public static void main(String[] args) { int[] testArr = {4,3,8,1,-1,2,5,4}; heapSort(testArr); for (int i = 0; i < testArr.length; i++) { System.out.println(testArr[i]); } }
堆排序时间复杂度/空间复杂度/稳定性
时间复杂度:O(N*logN), 更详细见上面代码中的注释。简单的理解是每次针对一个节点调整为堆的复杂度是O(logN)级别,需要调整N次,所以乘积可得。这么理解并不十分的精确,但大概意思正确,也比较好理解。
空间复杂度:O(1) ,只在交换的时候用了额外的一个空间。此处值得一提的是,在heapify方法中,我们这个版本的code使用了递归,由于递归的深度是logN级别,如果考虑递归栈,空间复杂度应该是O(logN),而不是O(1). 而这里的递归其实是可以改为迭代的。如下图所示:
private static void heapify(int[] tree, int n, int i) { while (i < n) { int maxi = i, lefti = 2*i + 1, righti = 2*i + 2; if(lefti < n && tree[lefti] > tree[maxi]) {maxi = lefti;} if(righti < n && tree[righti] > tree[maxi]) {maxi = righti;} if(i != maxi) { swap(tree, i, maxi); i = maxi; } else { break; } } }
稳定性:如果我们说一个排序算法是稳定的,那么是说相同的数字,在应用这个算法排序后,他们之间的相对位置保持不变。如果排序的对象只是数字,是不必在意这个的。但在实际的应用中,往往要排序的是一系列对象,按照某一个关键字排序,可能关键字相同,但是其他的内容不一样,这时候就有关系了。 举例来说,如果我们要排序的是班级学生和总成绩,我们先按照学号升序排序,然后按照成绩降序排序,如果成绩相同,我们希望学号小的排在前面。这时候稳定性就体现出来了,在第一次排序完学号靠前的学生,如果成绩与另一个学号靠后的学生相同,第二次按照成绩排序后我们仍然希望他排在前面。
堆排序不是稳定排序。见下面的例子,排序前红色的3在前面,排序后绿色的3在前面。
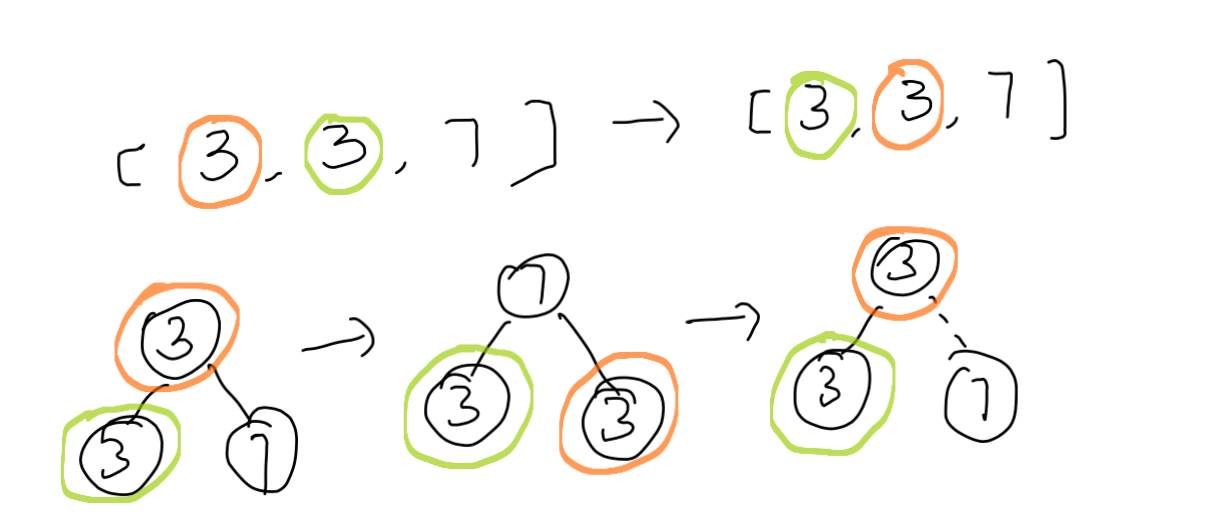
堆排序/堆适用场景
1. 在数据中寻找top(K)的操作。不需要都排序完成,只要做K次的堆调整即可。
2. 数据基本有序,比如数据在原始数组中的位置跟排好序之后的位置最多不超过K的情况。可以通过创建一个元素个数为K+1的小顶堆,不停地弹出堆顶元素,然后加入新的元素来完成排序。极大减少时间和空间复杂度。
3. 需要以O(1)的时间复杂度返回最大或者最小元素的时候,适合于优先级的情况。比如Java的PriorityQueue,默认的实现就是小顶堆。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号