一道题入门深度优先和广度优先遍历图

1 原题转载

废话不多说，直接上原题
这是洛谷的P5318

【深基18.例3】查找文献

题目描述

小K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个（也有可能没有）参考文献的链接指向别的博客文章。小K 求知欲旺盛，如果他看了某篇文章，那么他一定会去看这篇文章的参考文献（如果他之前已经看过这篇参考文献的话就不用再看它了）。

假设洛谷博客里面一共有 \(n(n\le10^5)\) 篇文章（编号为 1 到 \(n\)）以及 \(m(m\le10^6)\) 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章，请帮助小 K 设计一种方法，使小 K 可以不重复、不遗漏的看完所有他能看到的文章。

这边是已经整理好的参考文献关系图，其中，文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。

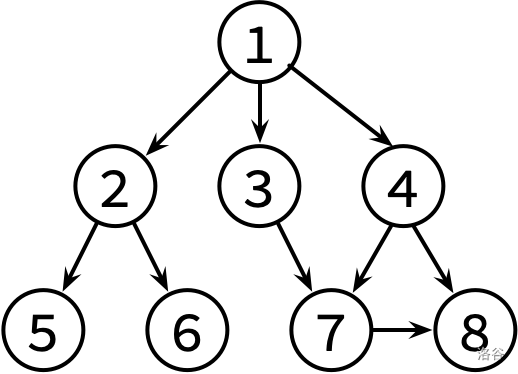
请对这个图分别进行 DFS 和 BFS，并输出遍历结果。如果有很多篇文章可以参阅，请先看编号较小的那篇(因此你可能需要先排序)。

输入格式

共 \(m+1\) 行，第 1 行为 2 个数，\(n\) 和 \(m\)，分别表示一共有 \(n(n\le10^5)\) 篇文章（编号为 1 到 \(n\)）以及\(m(m\le10^6)\) 条参考文献引用关系。

接下来 \(m\) 行，每行有两个整数 \(X,Y\) 表示文章 X 有参考文献 Y。

输出格式

共 2 行。
第一行为 DFS 遍历结果，第二行为 BFS 遍历结果。

样例 #1

样例输入 #1

8 9
1 2
1 3
1 4
2 5
2 6
3 7
4 7
4 8
7 8

样例输出 #1

1 2 5 6 3 7 8 4 
1 2 3 4 5 6 7 8

2 我的答案

#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int MAX =100010;

vector<int> g[MAX];
bool used[MAX],used2[MAX];

void dfs(int u){
    if(used[u]) return;
    used[u] = 1;
    cout<<u<<" ";
    for(auto e:g[u]) dfs(e);
}

void bfs(int u){
    queue<int> q;
    q.push(u);
    while(!q.empty()){
        int u =q.front();
        q.pop();
        if(used2[u]) continue;
        cout<<u<<" ";
        used2[u] =1;
        for(auto e:g[u]) q.push(e);
    }
}
int main(){
    int a,b;
    cin>>a>>b;
    for(int i = 1;i<=b;i++){
        int c,d;
        cin>>c>>d;
        g[c].push_back(d);
    }
    for(int i =1;i<=a;i++){
        sort(g[i].begin(),g[i].end());
    }
    dfs(1);
    cout<<endl;
    bfs(1);
}

3 讲解

这是很经典的一道图的遍历题，同时考察了深度优先遍历和广度优先遍历
所谓深度优先遍历就是所谓一条路走到黑，撞了南墙再回头，我们把根节点传入dfs函数，输出了根节点，再依次将其子节点传入dfs函数，每个子节点传入完后，再传入下一个，递归调用，就达到了深度优先的条件。
而广度优先则是要维护一个队列，先将根节点传入，再将其弹出，转而把其子节点全部压入队中，再从队首去取节点弹出，压入其根节点，如果压入重复的节点，则不输出，直到这个队列为空，那么也就遍历完成