[Leetcode]827.使用回溯+标记解决最大人工岛问题

在二维地图上， 0代表海洋， 1代表陆地，我们最多只能将一格 0 海洋变成 1变成陆地。

进行填海之后，地图上最大的岛屿面积是多少？（上、下、左、右四个方向相连的 1 可形成岛屿）

示例 1:

输入: [[1, 0], [0, 1]]
输出: 3
解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。

示例 2:

输入: [[1, 1], [1, 0]]
输出: 4
解释: 将一格0变成1，岛屿的面积扩大为 4。

示例 3:

输入: [[1, 1], [1, 1]]
输出: 4
解释: 没有0可以让我们变成1，面积依然为 4。

说明:

• 1 <= grid.length = grid[0].length <= 50
• 0 <= grid[i][j] <= 1

思路：

通过题目我们寻找一种遍历的方法，对每个数字0，判断如果将其填海，面积为多少，记为area。

用中文叙述就是：

area初始化为0
如果此海上面为陆地，area+上面连成片的陆地面积。
如果此海右面为陆地，area+右面连成片的陆地面积。
如果此海下面为陆地，area+下面连成片的陆地面积。
如果此海左面为陆地，area+左面连成片的陆地面积。

代码表示则是:

if(g[i-1][j]==1)area+=上面连成片的陆地面积;
if(g[i][j+1]==1)area+=右面连成片的陆地面积;
if(g[i+1][j]==1)area+=下面连成片的陆地面积;
if(g[i][j-1]==1)area+=左面连成片的陆地面积;

本题的目的就是找到这个最大的area。

可是遍历的时候会有两个麻烦点

1. 如果上下左右为连成一片的陆地呢，那按照上面的公式则会重复计算面积
2. 边界判断

其实2好解决，每次查询的时候进行边界检查即可。

但是1的解决方式就很复杂，我的解决方式是通过增加两个记录数组，给连成片的陆地进行编号，计算上下左右的陆地面积，若遇到有相同的陆地编号则不进行计算。

unsigned tag[50][50]={0};
/*用来记录第X,Y块属于哪块陆地片,如果是0则表示这块属于海洋，初始化全部为0*/
int area[700]={0};
/***
每个块号面积为多少，记作area[tag_number]=the_area_of_this tag
也可以用容器unordered_map<int,unsigned>area节省空间
***/

举个例子，比如有一海洋为(X,Y)，其中上面为陆地编号为1，右面为陆地(编号为1)，下面的陆地编号也为1(说明这块土地与(X,Y)上面那块土地相连)，左面为海(编号为0)
如下图画的，则area只用加一个标记为1的陆地面积其中一个就行了。

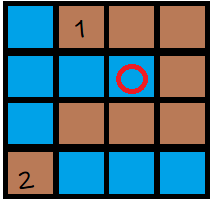
避开重复的数字有很多种方法，如unordered_map，或者建一个大小为4的数组，进行位运算这些都是一种方法，就不一一介绍了。

Solution

/*对代码解释在代码的后面*/
class Solution
{
  public:
    unsigned tag[50][50] = {0};
    int area[700] = {0};
    unsigned landNum = 0, X, Y;
    void search(const vector<vector<int>> &grid, const unsigned x, const unsigned y)
    {
        if (grid[x][y] == 1 && tag[x][y] == 0)
        {
            area[landNum]++;
            tag[x][y] = landNum;
            /*四个if是边界检查*/
            if (x >= 1)
                search(grid, x - 1, y);
            if (x < X - 1)
                search(grid, x + 1, y);
            if (y >= 1)
                search(grid, x, y - 1);
            if (y < Y - 1)
                search(grid, x, y + 1);
        }
    }
    int largestIsland(vector<vector<int>> &grid)
    {
        unsigned maxAnswer = 0, ans;
        X = grid.size();
        Y = grid[0].size();
        for (unsigned i = 0; i < X; i++)
        {
            for (unsigned j = 0; j < Y; j++)
            {
                if (grid[i][j] == 1 && tag[i][j] == 0)
                {
                    landNum++;
                    search(grid, i, j);
                }
            }
        }
        /*define the direction*/
        enum
        {
            UP = 0,
            RIGHT,
            DOWN,
            LEFT
        };
        unsigned tagIsland[4];
        unordered_map<unsigned,unsigned> count;

        for (unsigned i = 0; i < X; i++)
        {
            for (unsigned j = 0; j < Y; j++)
            {
                if (grid[i][j] == 0)
                {
                    ans = 1;
                    tagIsland[UP] = i >= 1 ? tag[i - 1][j] : 0;
                    tagIsland[RIGHT] = j < Y - 1 ? tag[i][j + 1] : 0;
                    tagIsland[DOWN] = i < X - 1 ? tag[i + 1][j] : 0;
                    tagIsland[LEFT] = j >= 1 ? tag[i][j - 1] : 0;
                    for (unsigned k = UP; k <= LEFT;k++){
                        if(count[tagIsland[k]]==0&&tagIsland[k]!=0){
                            ans += area[tagIsland[k]];
                            count[tagIsland[k]]=1;
                        }
                    }
                    maxAnswer = max(ans, maxAnswer);
                    count.clear();
                }
            }
        }
        if(maxAnswer==0)
            return X * Y;
        return maxAnswer;
    }
};

1. 我们首先通过search()函数对整个表进行回溯初始化，使所有单独的陆地都被编号。

2. 然后通过对每块海洋填海后的总area进行判断，保留最大面积maxAnswer，即每次计算出新的area后都有

   maxAnswer=area>maxAnswer?area:maxAnswer;
   

3. 在最后return前，如果maxAnswer=0则表示全部都是陆地，可以用反证法验证: 如果至少有一个海洋，maxAnswer至少为1。全是陆地的话只用return整片陆地的总面积即可，即X*Y。

至此，这道题的其中一种做法就完成了。