二分法和牛顿迭代法求平方根

实际上求平方根的算法方法主要有两种：二分法(binary search)和牛顿迭代法(Newton iteration)

二分法，以5为例

求根号5

a:折半：       5/2=2.5

b:平方校验:  2.5*2.5=6.25>5，并且得到当前上限2.5

c:再次向下折半:2.5/2=1.25

d:平方校验：1.25*1.25=1.5625<5,得到当前下限1.25

e:再次折半:2.5-(2.5-1.25)/2=1.875

f:平方校验：1.875*1.875=3.515625<5,得到当前下限1.875

 

每次得到当前值和5进行比较，并且记下下下限和上限，依次迭代，逐渐逼近平方根：

from math import sqrt

def sqrt_binary(n):

    sqrt1 = sqrt(n)  # 与库函数默认开方比对小数点
    y = n / 2  # n 第一次 二分以后的值，是移动在low和up之间的变量

    low = 0
    up = n

    count = 0  # count 迭代次数

    while abs(y - sqrt1) > 0.00000001:
        count += 1
        print(count, y)
        if y * y > n:
            up = y
            y = low + (up - low) / 2
        else:
            low = y
            y = up - (up - low) / 2

    return y


print(sqrt_binary(7))
print(sqrt(7))



# 1 3.5
# 2 1.75
# 3 2.625
# 4 3.0625
# 5 2.84375
# 6 2.734375
# 7 2.6796875
# 8 2.65234375
# 9 2.638671875
# 10 2.6455078125
# 11 2.64892578125
# 12 2.647216796875
# 13 2.6463623046875
# 14 2.64593505859375
# 15 2.645721435546875
# 16 2.6458282470703125
# 17 2.6457748413085938
# 18 2.6457481384277344
# 19 2.645761489868164
# 20 2.645754814147949
# 21 2.645751476287842
# 22 2.645749807357788
# 23 2.645750641822815
# 24 2.6457510590553284
# 25 2.645751267671585
# 26 2.6457513719797134
# 2.6457513198256493
# 2.6457513110645907

　　

牛顿迭代

 

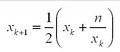
def sqrt_newton(n):
    
    sqrt1 = sqrt(n)  # 与库函数默认开方比对小数点
    y = n / 2  # n 第一次 二分以后的值，是移动在low和up之间的变量
    count = 0  # count 迭代次数

    while abs(y - sqrt1) > 0.00000001:
        count += 1
        print(count, y)
        y = (y + (n / y)) / 2

    return y


print(sqrt_newton(7))
print(sqrt(7))


# 1 3.5
# 2 2.75
# 3 2.6477272727272725
# 4 2.6457520483808037
# 2.6457513110646933
# 2.6457513110645907

　　

牛顿法只迭代了3次，而二分法迭代了26次

牛顿法开三次方

def cube_newton(num):
    x = num / 3
    y = 0
    count = 1
    while abs(x - y) > 0.00000001:
        print(count, x)
        count += 1
        y = x
        x = (2 / 3) * x + num / (x * x * 3)
    return x


print(cube_newton(27))

　

你只想敲代码，然而你确需要数学。

原文地址：http://blog.csdn.net/ycf74514/article/details/48996383