【信息安全数学基础】Fermat素性检测
算法背景与原理：
1、Fermat小定理：给定素数p，a∈Z，则有a^(p-1)%p=1
2、Fermat素性检测算法：奇整数m，若任取一整数2<=a<=m-2，gcd（a，m）=1，使得a^(m-1)%m=1，则m至少有1/2的概率为素数
算法步骤：
1、从文本中读取数字作为待判定的大数m
2、给出安全参数k
3、随机选取整数a，满足a∈[2,m-2]
4、计算g=gcd（a，m），如果g=1进行下一步，否则不是素数跳出
5、计算r=a^(m-1)%m，如果r=1则m可能是素数，否则不是素数跳出
6、重复上述过程k次，如果每次判定m都可能是素数，那么m是素数的概率是1-1/2^k
代码设计及注释：
1 extern "C" 2 { 3 #include<miracl.h> 4 #include<mirdef.h> 5 } 6 #include <stdio.h> 7 8 int main() 9 { 10 FILE *fp; 11 int i = 0, k, probability = 1;//k是安全参数，pr是概率 12 printf("请输入安全参数k："); 13 scanf("%d",&k); 14 big m, r, g, a, b, m_4; 15 miracl *mip = mirsys(4000, 10);//初始化MIRACL系统,4000位的10进制数 16 m = mirvar(0);//big类型初始化函数 17 m_4 = mirvar(0); 18 r = mirvar(0); 19 g = mirvar(0); 20 a = mirvar(0); 21 b = mirvar(1); 22 fp = fopen("20.txt", "r+"); 23 mip->IOBASE = 10; 24 cinnum(m, fp);//将大数字符串转换成大数 25 fclose(fp); 26 //奇数m,若取任意整数2<=a<=m-2，gcd（a，m）=1，使得a^(m-1)=1（mod m），则m有1/2的概率为素数 27 for (i = 0;i<k;i++) 28 { 29 probability = probability * 2; 30 decr(m, 4, m_4);//m_4=m-4 31 bigrand(m_4, a);//产生一个小于m-4的大数随机数a 32 printf("随机数a="); 33 cotnum(a, stdout); 34 incr(a, 2, a);//a=a+2，这样可以保证a>=2且a<=m-2 35 decr(m, 1, g);//g=m-1，作为计算模的指数 36 powmod(a, g, m, r);//r=a^g （mod m），如果r=1，那么m就有二分之一的概率为素数 37 egcd(a, m, g);//g=gcd(a,m) 38 if (mr_compare(g, b) || mr_compare(b, r))//如果gcd(a,m)不等于1或模值r不等于1，不是素数，跳出 39 { 40 printf("gcd(a.m)不等于1或r不等于1\n"); 41 break; 42 } 43 else 44 printf("最大公约数为1，模值为1，因此输入有%d/%d可能为素数\n",probability - 1, probability); 45 } 46 printf("由此可得所输入的数字：\n"); 47 cotnum(m, stdout);//输出m 48 if (i == k) 49 printf("有%d/%d的可能性输入的是素数\n",probability - 1, probability); 50 else 51 puts("不是素数\n"); 52 mirexit(); 53 return 0; 54 }
以验收数据10、20，安全参数k=5为例
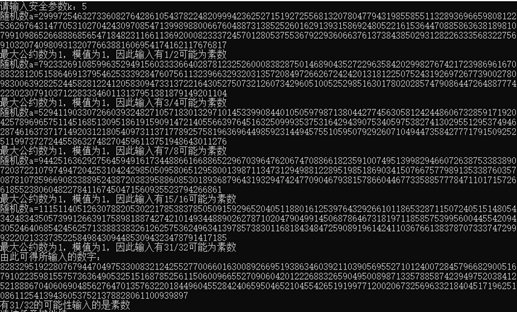
第10个验收数据在k次运算之后符合判断条件，因此有31/32的概率是素数
第20个验收数据在第一次判定就发生错误，因此不是素数
