[模板]ST表浅析

ST表，稀疏表，用于求解经典的RMQ问题。即区间最值问题。

Problem：

给定n个数和q个询问，对于给定的每个询问有l,r，求区间[l,r]的最大值。.

Solution:

主要思想是倍增和区间dp。

状态：dp[i][j] 为闭区间[i,i+2^j-1]的最值。

这个状态与转移方程的关系很大，即闭区间的范围涉及到了转移方程的简便性。

转移方程：dp[i][j]=max(dp[i][j-1],dp[i+2^(j-1)][j-1])。

这是显然的，但这里有个细节：第一个项的范围为[i,i+2^(j-1)-1]，即第i个数到第i+2^(j-1)个数的前一个数，而第二个项的范围是[i+2^(j-1),i+2^j-1]。这里容易弄混，所以导致无法理解整个方程，或者写错。

询问：[l,r]区间的最大值。

令g=log2(r-l+1)向下取整。则区间的最值就是max(dp[l][g],dp[r-2^g+1][g])。

好的，我们开始对这些方程做一番分析。假设现在有5个数，为如下情况。这些分别是，dp[1][0],dp[2][0]....dp[5][0]

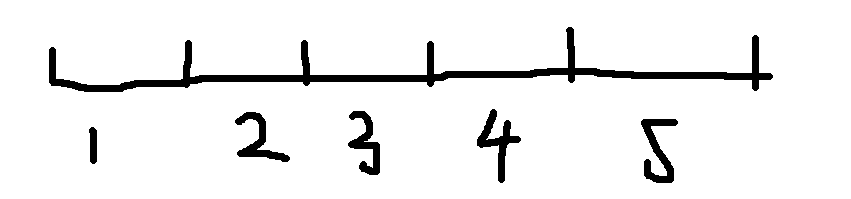
接着，我们可以统计到红色区域的最大值。这些分别是dp[1][1],dp[2][1]...dp[4][1]

 最后，我们再统计到dp[1][2],dp[2][2]，也就是1~1+4-1和2~2+4-1的最大值。

 

直到整个求完。（5后面的点因为皆为0，所以在取区间最大值的时候可以直接忽略）

有了这些后，如果要求l~r的最大值，我们需要让两个区间覆盖这个区间。假设我们询问1~5的最大值。

按道理来讲，我们假设2^x=5-1+1，然后dp[1][x]不就完事了？然而很可惜，x可能为小数。因此，x我们应当向下取整x'，那么显然这样子取dp[1][x']会比dp[1][x]少一段。

于是我们再采用dp[5-2^x'+1][x']的方式来弥补。什么意思呢？

 

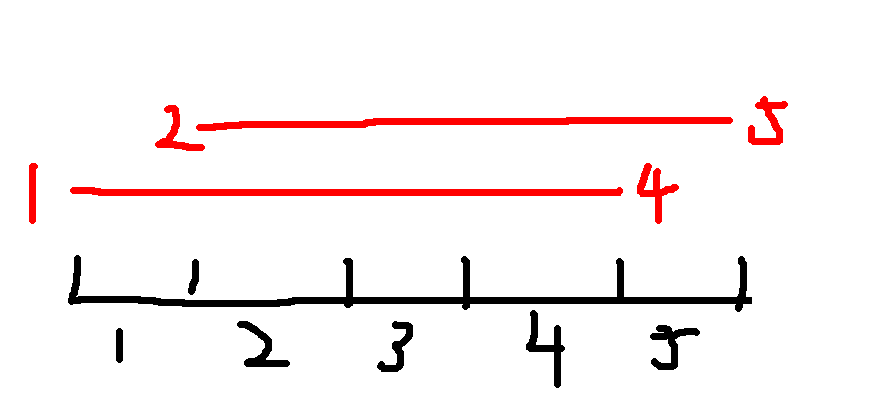
像这样，在两个互相被覆盖的区间里取一个最大值，是不是完美的解决了这个问题呢？而这个x就等于log2(x)，x'即为log2(x)向下取整。

你可能会说这样有没有可能会没有全部覆盖，这很显然不可能。因为l+2^x'<r-2^x' 等价于 2^(x'+1)<r-l。而显然这个x'+1>=x，所以2^(x‘+1)>2^x=r-l+1>r-l。因此原不等式绝对不成立。

以上，ST表是一个很好的倍增思想入门。在LCA中也用到了与ST表非常类似的倍增思想。

ST表很简单。请注意常数，很容易就会了。Luogu P3865即为模板题。

下面是代码：

#include<bits/stdc++.h>
using namespace std;
template <typename T> T gn(T &x){
    x=0;
    T plus=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')plus=(ch=='-'?-1:1),ch=getchar();
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*plus;
}
const int N=1e5+10;
int a[N][25];
template <typename T> inline int mmax(T &a,T &b){return a<b?b:a;}
inline int dpow(int a,int x){
    int ret=1;
    while(x){
        if(x&1)ret*=a;
        a*=a;
        x>>=1;
    }
    return ret;
}

int main(){
    int n,m;
    gn(n),gn(m);
    for(int i=1;i<=n;i++)
        gn(a[i][0]);
    int plus=1;
    for(int j=1;j<25;j++){
        for(int i=1;i+plus<=n;i++)
            a[i][j]=mmax(a[i][j-1],a[i+plus][j-1]);
        plus*=2;
    }
    int na,nb,x;
    for(int i=0;i<m;i++){
        gn(na),gn(nb);
        x=log2(nb-na+1);
        printf("%d\n",mmax(a[na][x],a[nb-dpow(2,x)+1][x]));
    }
    return 0;
}