[模板]LCA的倍增求法解析
题目描述
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
输入输出格式
输入格式:
第一行包含三个正整数N、M、S,分别表示树的结点个数、询问的个数和树根结点的序号。
接下来N-1行每行包含两个正整数x、y,表示x结点和y结点之间有一条直接连接的边(数据保证可以构成树)。
接下来M行每行包含两个正整数a、b,表示询问a结点和b结点的最近公共祖先。
输出格式:
输出包含M行,每行包含一个正整数,依次为每一个询问的结果。
输入输出样例
5 5 4 3 1 2 4 5 1 1 4 2 4 3 2 3 5 1 2 4 5
4 4 1 4 4
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
样例说明:
该树结构如下:

第一次询问:2、4的最近公共祖先,故为4。
第二次询问:3、2的最近公共祖先,故为4。
第三次询问:3、5的最近公共祖先,故为1。
第四次询问:1、2的最近公共祖先,故为4。
第五次询问:4、5的最近公共祖先,故为4。
故输出依次为4、4、1、4、4。
Solution:
题目来源:Luogu P3379
我们来讲讲LCA的倍增求法,来自于LS学长神犇的教授,加上我自身的理解,可能对各位新人的帮助会更有理解作用,所以我决定分享一下。(蒟蒻一本正经)
LCA——最近公共祖先。最朴素的算法无疑是从两个点一个个往上走,出现的第一个两个点都走过的点即为两点的LCA。这个无需多加解释。
然而这样时间复杂度非常高。尤其是当树退化成一条链的时候,每次查询的复杂度将会飙到O(N)。
为此,倍增的作用就是将两点上升所需的复杂度减低。而原理就是,把两点往上跳,跳到LCA.-.
流程概括为:将深度不同的两点跳到同一层(深一点的跳到浅一点的一层),然后再将两点向上跳到LCA的下面一层,最后再向上跳一层。(后面一部分下面会解释,为什么不能直接跳到LCA。)
快速跳的方法,每次向上跳的层数都为2^i层。(i为非负整数),相当于把层数差转成2进制数,一位一位往上跳,使层数差快速减小。这样,每次查询复杂度最高就只会为log2(N)。
实现方法:
我们首先需要两个数组。f[i][j]代表从i点向上跳2^j层后所到达的点,dep[i]代表这棵树中点i的深度。
dep数组可以在从根深度遍历整棵树的时候求得。
f数组利用了递推的思想。递推式为:f[i][j]=f[f[i][j-1]][j-1]。初始化f[i][0]也可以在遍历整棵树的时候求得。
之后,我们处理LCA时,按照上面的流程。我们先将较深的点一次次往上逼近较浅的点,直至他们层数相同。(相当于把层数差的二进制一位一位减去,直至变成0)
然后,两点再同时向上逼近。i从最高位开始枚举,假设两点分别为x,y,那么能向上跳的判断式为:if f[x][i]!=f[y][i] then x=f[x][i],y=f[y][i]。翻译成人话就是如果两点向上跳了2^i层以后不到同一个点就接着往上跳。为什么这样?因为如果往上跳了2^i层,即使到了同一个点,它不一定是两点的LCA。(为什么?)
这样做,最终就会到达LCA的下面一层。随后,我们再将两点向上跳一层。LCA求得。
为什么最终会到达LCA的下面一层?
我们假设从a,b点开始,往上跳2^j层,跳到同一点。不跳。往上跳2^(j-1)层,不跳到同一点,往上跳,分别到了A',B'。显然,这种情况是一定会存在的。
那么,从A',B’再往上跳到原来那个决定不跳的点,显然要跳2^(j-1)层。那么,那个点有可能是LCA,也有可能不是,对吧?所以,从A',B'往上跳到LCA所需的层数,是≤2^(j-1)的。
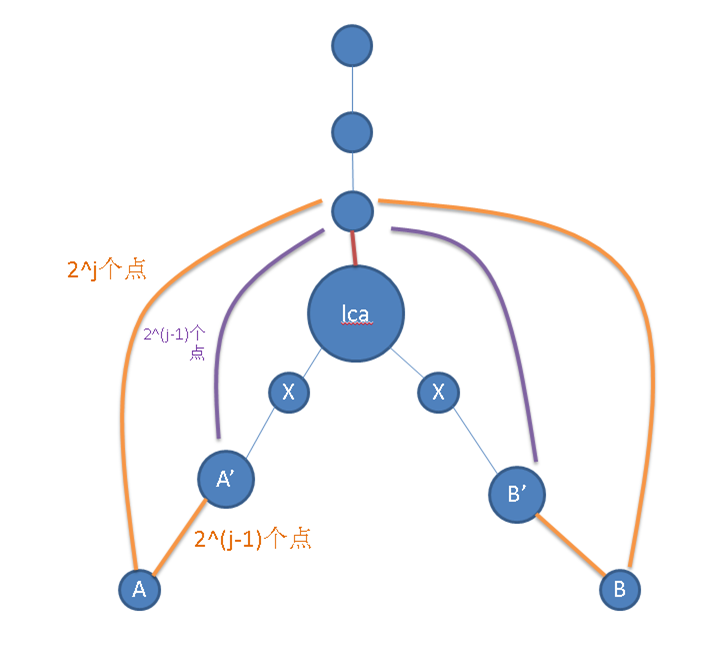
所以,从A',B'跳到LCA的下面一层X的所需层数,会是<2^(j-1)的。换句话来说,A',B'到X的层数变成了一个j-2位的二进制数(可能会有前导零,也就是还可能会跳到点数相同的地方)。而此时,刚好枚举到j-2位。那么,前导零不减,再这么减下去,你发现,这个层数差最终会变成0,而你最终也会到达第X层。(为什么?)
如果不懂,也可以先放着。你只需要知道这么做可以到LCA的下面一层就OK了orz
请最好自己手画一棵树模拟一下整个算法的过程。
蒟蒻解释难免有错误,如果出现错误,请回复我,我将感激不尽orz
代码如下:
#include<bits/stdc++.h> using namespace std; const int N=500010,OP=log2(500000)+1; int dpt[N][26]; int dep[N]; int gi(){ int x=0; char ch=getchar(); while(ch<'0'||ch>'9')ch=getchar(); while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar(); return x; } int h[N],to[N*2],nexp[N*2],p=1; inline void ins(int a,int b){ nexp[p]=h[a],h[a]=p,to[p]=b,p++; } void dfs(int p,int x){ dep[x]=p; for(int u=h[x];u;u=nexp[u]){ if(!dep[to[u]]){ dpt[to[u]][0]=x; dfs(p+1,to[u]); } } } int LCA(int a,int b){ if(dep[a]<dep[b])swap(a,b); for(int j=OP;j>=0;j--) if(dep[a]-(1<<j)>=dep[b])a=dpt[a][j]; if(a!=b){ for(int j=OP;j>=0;j--) if(dpt[a][j]!=dpt[b][j])a=dpt[a][j],b=dpt[b][j]; a=dpt[a][0]; } return a; } int main(){ int n,q,r; cin>>n>>q>>r; int a,b; for(int i=0;i<n-1;i++){ a=gi(),b=gi(); ins(a,b),ins(b,a); } dfs(1,r); for(int j=1;j<=OP;j++) for(int i=1;i<=n;i++) dpt[i][j]=dpt[dpt[i][j-1]][j-1]; for(int i=0;i<q;i++){ a=gi(),b=gi(); printf("%d\n",LCA(a,b)); } return 0; }
为什么与X层数差最终会变成0?
假设你已经会写这个算法了。
首先我们证明,前导零不会被减去。假设与X层的层数差为x',而你正准备往上跳y层。由于LCA的层数是X+1,而LCA往上的点它都不会跳,对吧?(反而,如果LCA往下的点,也就是层数<=X,也就是y<x'+1,它都会往上跳)所以如果y>=x'+1,那么就绝对不会往上跳。
显然,当x'的该位为0,且属于前导零,那么只需证明x'+1<=y。而这个非常易证(假设y为10000,而x'满足条件的最大值为01111)。所以保证,前导零是不会减去的。
接着我们证明,一旦枚举到了x'的第一个为1的位数,这个1绝对会被减去。按照同样的方法,假设y为10000,而x'满足条件的最小值为10000,所以y<x'+1.
两点合在一起,前导零不会减去,枚举到一个1位就减去,最终这个层数差就会变成0.证毕。


