Codeforces Round #236 (Div. 2)
You have a nuts and lots of boxes. The boxes have a wonderful feature: if you put x (x ≥ 0) divisors (the spacial bars that can divide a box) to it, you get a box, divided into x + 1 sections.
You are minimalist. Therefore, on the one hand, you are against dividing some box into more than k sections. On the other hand, you are against putting more than v nuts into some section of the box. What is the minimum number of boxes you have to use if you want to put all the nuts in boxes, and you have b divisors?
Please note that you need to minimize the number of used boxes, not sections. You do not have to minimize the number of used divisors.
The first line contains four space-separated integers k, a, b, v (2 ≤ k ≤ 1000; 1 ≤ a, b, v ≤ 1000) — the maximum number of sections in the box, the number of nuts, the number of divisors and the capacity of each section of the box.
Print a single integer — the answer to the problem.
3 10 3 3
2
3 10 1 3
3
100 100 1 1000
1
题意:就是给几个挡板,还有每个曹最多放坚果的数量,求最少用几个盒子。
ps:很坑爹的水体,wa3发,最后还是水过的,我是直接模拟
2 #include <cstring>
3 #include <algorithm>
4 typedef long long ll;
5 const int MAX = ;
6 int main()
7 {
8 int k,a,v,b; int cnt=0;
9 while(scanf("%d %d %d %d",&k,&a,&v,&b)==4)
10 {
11 int n=a/v;
12 if(a%v!=0) n++;
13 if(n<=b+1)
14 {
15 if(b%k==0) printf("%d\n",b/k);
16 else printf("%d\n",b/k+1);
17 }
18 else
19 {
20 if((b+1)%k==0) cnt+=(b+1)/k,n-=cnt;
21 else cnt+=(b+1)/k+1,n-=cnt;
22 if(n<=0) printf("%d",cnt);
23 else
24 {
25 if(n%k==0) cnt+=n/k;
26 else cnt+=n/k+1;
27 printf("%d\n",cnt);
28 }
29
30 }
31
32 }
33 return 0;
34 }
The Queen of England has n trees growing in a row in her garden. At that, the i-th (1 ≤ i ≤ n) tree from the left has height ai meters. Today the Queen decided to update the scenery of her garden. She wants the trees' heights to meet the condition: for all i (1 ≤ i < n), ai + 1 - ai = k, wherek is the number the Queen chose.
Unfortunately, the royal gardener is not a machine and he cannot fulfill the desire of the Queen instantly! In one minute, the gardener can either decrease the height of a tree to any positive integer height or increase the height of a tree to any positive integer height. How should the royal gardener act to fulfill a whim of Her Majesty in the minimum number of minutes?
The first line contains two space-separated integers: n, k (1 ≤ n, k ≤ 1000). The second line contains n space-separated integers a1, a2, ..., an(1 ≤ ai ≤ 1000) — the heights of the trees in the row.
In the first line print a single integer p — the minimum number of minutes the gardener needs. In the next p lines print the description of his actions.
If the gardener needs to increase the height of the j-th (1 ≤ j ≤ n) tree from the left by x (x ≥ 1) meters, then print in the corresponding line "+ j x". If the gardener needs to decrease the height of the j-th (1 ≤ j ≤ n) tree from the left by x (x ≥ 1) meters, print on the corresponding line "- j x".
If there are multiple ways to make a row of trees beautiful in the minimum number of actions, you are allowed to print any of them.
4 1
1 2 1 5
2
+ 3 2
- 4 1
4 1
1 2 3 4
0
题意:给出一组数列求使得这个数列公差为k对树操作的最小次数。
sl:直接模拟第一个数字。貌似还可以 枚举数列中的每个数字。
2 #include <cstring>
3 #include <algorithm>
4 #include<cmath>
5 typedef long long ll;
6 const int MAX = 1e3+10;
7 int a[MAX],b[MAX],temp[MAX][MAX],vis[MAX][MAX];
8 int x[MAX][MAX];
9 int con[MAX];
10 int main()
11 {
12 int n,k,ans; int flag;
13 while(scanf("%d %d",&n,&k)==2)
14 {
15 ans=10000; int cnt=0; int cur=0;
16 for(int i=0;i<n;i++) scanf("%d",&a[i]);
17 for(int i=1;i<MAX;i++)
18 {
19 memset(b,0,sizeof(b)); b[0]=i; cnt=0; cur=0;
20 for(int j=1;j<n;j++)
21 {
22 b[j]=b[j-1]+k;
23 }
24 for(int j=0;j<n;j++)
25 {
26 if(b[j]!=a[j])
27 {
28 cnt++;
29 if(b[j]>a[j])
30 {
31 temp[i][cur]=j;
32 x[i][cur]=abs(b[j]-a[j]);
33 vis[i][cur++]=1;
34
35 }
36 else
37 {
38 temp[i][cur]=j;
39 x[i][cur]=abs(b[j]-a[j]);
40 vis[i][cur++]=0;
41 }
42 }
43 }
44 con[i]=cur;
45 if(cnt<ans)
46 {
47 ans=cnt;
48 flag=i;
49 }
50 }
51 if(ans==0) printf("0\n");
52 else
53 {
54 printf("%d\n",ans);
55 for(int i=0;i<con[flag];i++)
56 {
57 if(vis[flag][i]==0) printf("- ");
58 else printf("+ ");
59 printf("%d ",temp[flag][i]+1);
60 printf("%d\n",x[flag][i]);
61 }
62 }
63 }
64 return 0;
65 }
Let's call an undirected graph of n vertices p-interesting, if the following conditions fulfill:
- the graph contains exactly 2n + p edges;
- the graph doesn't contain self-loops and multiple edges;
- for any integer k (1 ≤ k ≤ n), any subgraph consisting of k vertices contains at most 2k + p edges.
A subgraph of a graph is some set of the graph vertices and some set of the graph edges. At that, the set of edges must meet the condition: both ends of each edge from the set must belong to the chosen set of vertices.
Your task is to find a p-interesting graph consisting of n vertices.
The first line contains a single integer t (1 ≤ t ≤ 5) — the number of tests in the input. Next t lines each contains two space-separated integers: n,p (5 ≤ n ≤ 24; p ≥ 0; 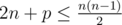 ) — the number of vertices in the graph and the interest value for the appropriate test.
) — the number of vertices in the graph and the interest value for the appropriate test.
It is guaranteed that the required graph exists.
For each of the t tests print 2n + p lines containing the description of the edges of a p-interesting graph: the i-th line must contain two space-separated integers ai, bi (1 ≤ ai, bi ≤ n; ai ≠ bi) — two vertices, connected by an edge in the resulting graph. Consider the graph vertices numbered with integers from 1 to n.
Print the answers to the tests in the order the tests occur in the input. If there are multiple solutions, you can print any of them.
1
6 0
1 2
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6
题意:给出定点的个数,对点连边,使得满足题目中所述
sl:很容易想到是贪心加构造。每轮从n个点里挑两个点进行连边即可 ,数据很小完全可以
2 #include <cstring>
3 #include <algorithm>
4 typedef long long ll;
5 const int MAX = 1000;
6 int vis[MAX][MAX]; int v1[MAX],v2[MAX];
7 int e[MAX][MAX];
8 int main()
9 {
10 int cas; int n,p;
11 scanf("%d",&cas);
12 while(cas--)
13 {
14 scanf("%d %d",&n,&p);
15 memset(vis,0,sizeof(vis));
16 memset(e,0,sizeof(e));
17 int cnt=0;
18 int flag=1;
19 while(cnt<2*n+p)
20 {
21 memset(v1,0,sizeof(v1));
22 for(int i=1;i<=n&&flag;i++)
23 {
24 for(int j=1;j<=n&&flag;j++)
25 {
26 if(i!=j&&!vis[i][j]&&!v1[i]&&!v1[j]&&!vis[j][i])
27 {
28 vis[i][j]=vis[j][i]=1;
29 cnt++;
30 if(cnt==2*n+p) flag=0;
31 }
32 }
33 }
34 }
35 for(int i=1;i<=n;i++)
36 {
37 for(int j=i+1;j<=n;j++)
38 {
39 if(vis[i][j]) printf("%d %d\n",i,j);
40 }
41 }
42 }
43 return 0;
44 }
You have an array of positive integers a[1], a[2], ..., a[n] and a set of bad prime numbers b1, b2, ..., bm. The prime numbers that do not occur in the set b are considered good. The beauty of array a is the sum 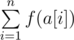 , where function f(s) is determined as follows:
, where function f(s) is determined as follows:
- f(1) = 0;
- Let's assume that p is the minimum prime divisor of s. If p is a good prime, then
![]() , otherwise
, otherwise ![]() .
.
You are allowed to perform an arbitrary (probably zero) number of operations to improve array a. The operation of improvement is the following sequence of actions:
- Choose some number r (1 ≤ r ≤ n) and calculate the value g = GCD(a[1], a[2], ..., a[r]).
- Apply the assignments:
![]() ,
, ![]() , ...,
, ..., ![]() .
.
What is the maximum beauty of the array you can get?
The first line contains two integers n and m (1 ≤ n, m ≤ 5000) showing how many numbers are in the array and how many bad prime numbers there are.
The second line contains n space-separated integers a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 109) — array a. The third line contains m space-separated integers b1, b2, ..., bm (2 ≤ b1 < b2 < ... < bm ≤ 109) — the set of bad prime numbers.
Print a single integer — the answer to the problem.
5 2
4 20 34 10 10
2 5
-2
4 5
2 4 8 16
3 5 7 11 17
10
题意:就是给出数组a,和数组b,求一个good number ,每次可以对a进行操作,操作是将a的1-i项除以其gcd;
sl:从后向前扫一遍求出所有的公约数,每一个都要进行一次判断,判断其最小因子是不是在b中如果在结果减1不在加1判断这个公约数是不是合适
不合适则将其约去即可。(参看别人代码了)
You have matrix a of size n × n. Let's number the rows of the matrix from 1 to n from top to bottom, let's number the columns from 1 to n from left to right. Let's use aij to represent the element on the intersection of the i-th row and the j-th column.
Matrix a meets the following two conditions:
- for any numbers i, j (1 ≤ i, j ≤ n) the following inequality holds: aij ≥ 0;
![]() .
.
Matrix b is strictly positive, if for any numbers i, j (1 ≤ i, j ≤ n) the inequality bij > 0 holds. You task is to determine if there is such integer k ≥ 1, that matrix ak is strictly positive.
The first line contains integer n (2 ≤ n ≤ 2000) — the number of rows and columns in matrix a.
The next n lines contain the description of the rows of matrix a. The i-th line contains n non-negative integers ai1, ai2, ..., ain (0 ≤ aij ≤ 50). It is guaranteed that 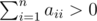 .
.
If there is a positive integer k ≥ 1, such that matrix ak is strictly positive, print "YES" (without the quotes). Otherwise, print "NO" (without the quotes).
2
1 0
0 1
NO
5
4 5 6 1 2
1 2 3 4 5
6 4 1 2 4
1 1 1 1 1
4 4 4 4 4
YES
题意:问矩阵A^k是不是每项都正
sl:很简单的图论题目,比赛时没想明白,被矩阵给蒙住了,把矩阵华为图,就是求对于图上如果存在某两点不可达那么一定是NO因为开始那两个点就没边
之后的k次方是指两点存在一条长为k的路径,所以求下强连通就好了
2 #include <cstring>
3 #include <vector>
4 #include <algorithm>
5
6 using namespace std;
7
8 vector <int> G[2002], rG[2002], t;
9 int vis[2002];
10 void add_edge(int from , int to)
11 {
12 G[from].push_back(to);
13 rG[to].push_back(from);
14 }
15 void dfs(int s){
16 vis[s]=1;
17 for(int i=0; i<G[s].size();i++)
18 {
19 if(!vis[G[s][i]])
20 dfs(G[s][i]);
21 }
22 t.push_back(s);
23 }
24
25 void rdfs(int s, int k){
26 vis[s]=k;
27 for(int i=0; i<rG[s].size(); i++)
28 {
29 if(!vis[rG[s][i]])
30 rdfs(rG[s][i],k);
31 }
32 }
33
34 int main()
35 {
36 int n, x; int sccno=0;
37 scanf("%d",&n);
38 for(int i=0; i<n; i++) for(int j=0; j<n; j++)
39 {
40 scanf("%d",&x);
41 if(x)
42 {
43 add_edge(i,j);
44 }
45 }
46 memset(vis,0,sizeof(vis));
47 for(int i=0; i<n; i++)
48 if(!vis[i]) dfs(i);
49 memset(vis,0,sizeof(vis));
50 for(int i=n-1; i>=0; i--)
51 {
52 if(!vis[t[i]])
53 {
54 ++sccno;
55 rdfs(t[i],sccno);
56
57 }
58 }
59
60 if( sccno== 1 ) puts("YES");
61 else puts("NO");
62 }


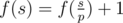 , otherwise
, otherwise 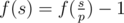 .
.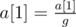 ,
, 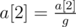 ,
, 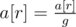 .
.
 浙公网安备 33010602011771号
浙公网安备 33010602011771号