Codeforces Round #232 (Div. 2) On Sum of Fractions
Let's assume that
- v(n) is the largest prime number, that does not exceed n;
- u(n) is the smallest prime number strictly greater than n.
Find 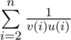 .
.
Input
The first line contains integer t (1 ≤ t ≤ 500) — the number of testscases.
Each of the following t lines of the input contains integer n (2 ≤ n ≤ 109).
Output
Print t lines: the i-th of them must contain the answer to the i-th test as an irreducible fraction "p/q", where p, q are integers, q > 0.
Sample test(s)
input
2
2
3
output
1/6
7/30
分析:把公式分解1/(p*q)=1/(p-q) * (1/q-1/p) 然后求和发现公式:ans=(-2q+2*n-2*p+2+2*q*q)/(2*u*v);
1 #include<cstdio>
2 #include<cmath>
3 #include<algorithm>
4 using namespace std;
5 bool isprime(unsigned long long x)
6 {
7 int idx=sqrt(x);
8 for(int i=2; i<=idx; ++i)
9 if(x%i==0)
10 return false;
11 return true;
12 }
13 int main()
14 {
15 int t;
16 unsigned long long n;
17 scanf("%d",&t);
18 while(t--)
19 {
20 scanf("%I64u",&n);
21 unsigned long long v=n,u=n+1;
22 while(!isprime(v))
23 --v;
24 while(!isprime(u))
25 ++u;
26 unsigned long long p=v*u-2*u+2*n-2*v+2,q=2*v*u,tmp=__gcd(p,q);
27 printf("%I64u/%I64u\n",p/tmp,q/tmp);
28 }
29 }
2 #include<cmath>
3 #include<algorithm>
4 using namespace std;
5 bool isprime(unsigned long long x)
6 {
7 int idx=sqrt(x);
8 for(int i=2; i<=idx; ++i)
9 if(x%i==0)
10 return false;
11 return true;
12 }
13 int main()
14 {
15 int t;
16 unsigned long long n;
17 scanf("%d",&t);
18 while(t--)
19 {
20 scanf("%I64u",&n);
21 unsigned long long v=n,u=n+1;
22 while(!isprime(v))
23 --v;
24 while(!isprime(u))
25 ++u;
26 unsigned long long p=v*u-2*u+2*n-2*v+2,q=2*v*u,tmp=__gcd(p,q);
27 printf("%I64u/%I64u\n",p/tmp,q/tmp);
28 }
29 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号