基于校园网络问题的最小生成树的两种算法

题目背景：

　　学校有10个学院，3个研究所，1个大型图书馆，4所实验室，现在知道他们之间的距离，想在他们之间建设网线，求最小的花费

这题暑假根本没看，不过最近正好在研究图论和树，今晚就不打游戏了，继续写博客提升自己的认识水平吧。

拿到这题一看就知道要求最小的花费，肯定是最小生成树问题了啊，最小生成树问题不存在环路的，也就是当前节点不可能通过自身或者别的节点回到自己

如何保证不能回到自身节点呢？

我们采用一种放法，叫做避圈法：在生成树的过程中，我们把已经生成树中的节点看成一个集合，把剩下的节点看成另一个集合，从连接两个集合中选取最小边即可（这里的集合就是连通分量）

最小生成树有两种算法：Prim算法和kruskal算法

首先我们先说说Prim算法：

　　Prim算法步骤：

　　我直接附上一张到来的图吧

 

 步骤

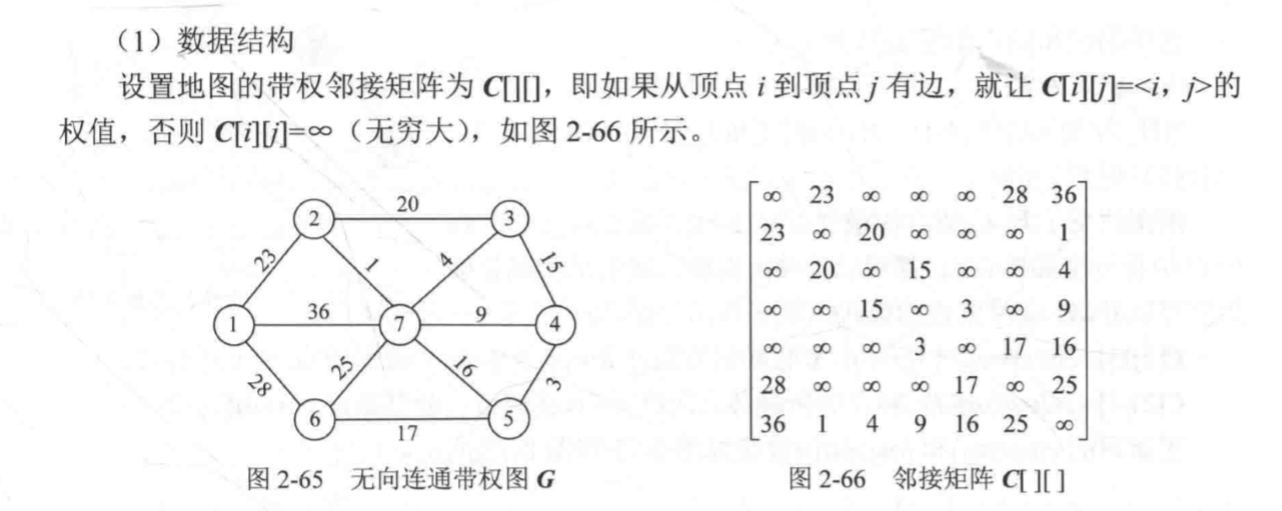
　　1： 确定合适的数据结构用邻接矩阵来存储图，就是矩阵的存储图的权值，要是存在边（u，x）那么G（u，x）=边上权值，bool 数组s[],如果s[i]=true；表示定点i加入了集合V

　　　　从图上可以直观地看出那些是最小的边，但是如何实现呢？这里可以设置两个数组，一个closeset[j],用来表示u-v中的定点j到达集合U最近的节点，另一个数组为lowcost[j]表示

　　　　v-u集合中定点j到达集合u的最小权值

　　2：初始化邻接矩阵G，数组closest[]，lowcost[]和s[]

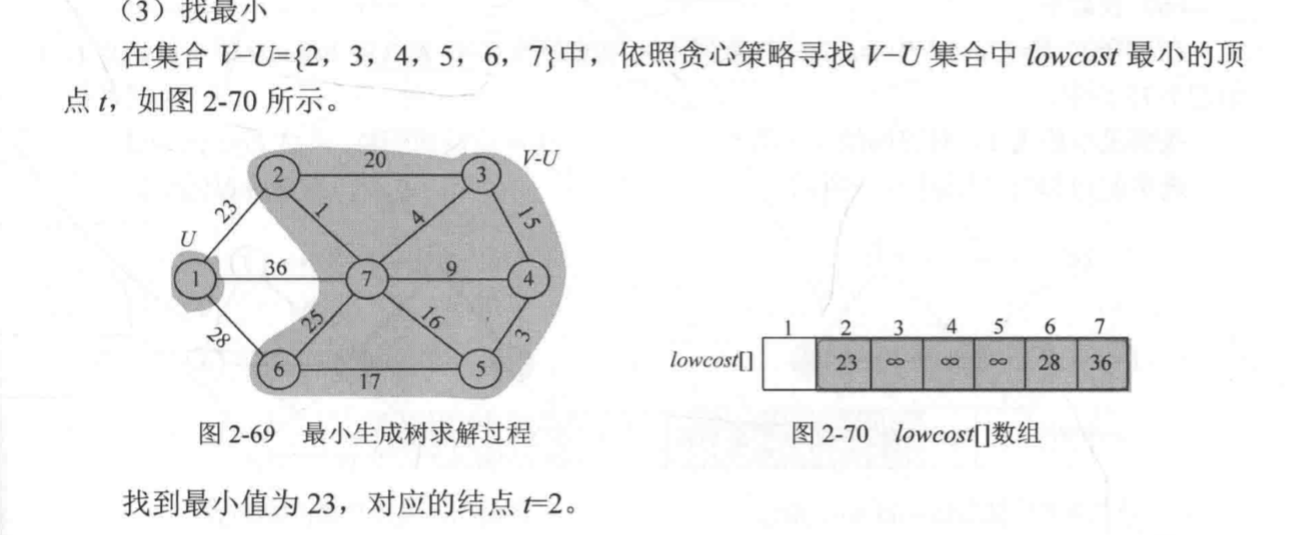
　　3：从定点u0开始，寻找距离u0最近的v-u集合中的顶点t，并更新两个数组和一个s数组

　　4：将顶点t加入集合u中

　　5：如果集合v-u，算法结束，否则，跳转步骤6

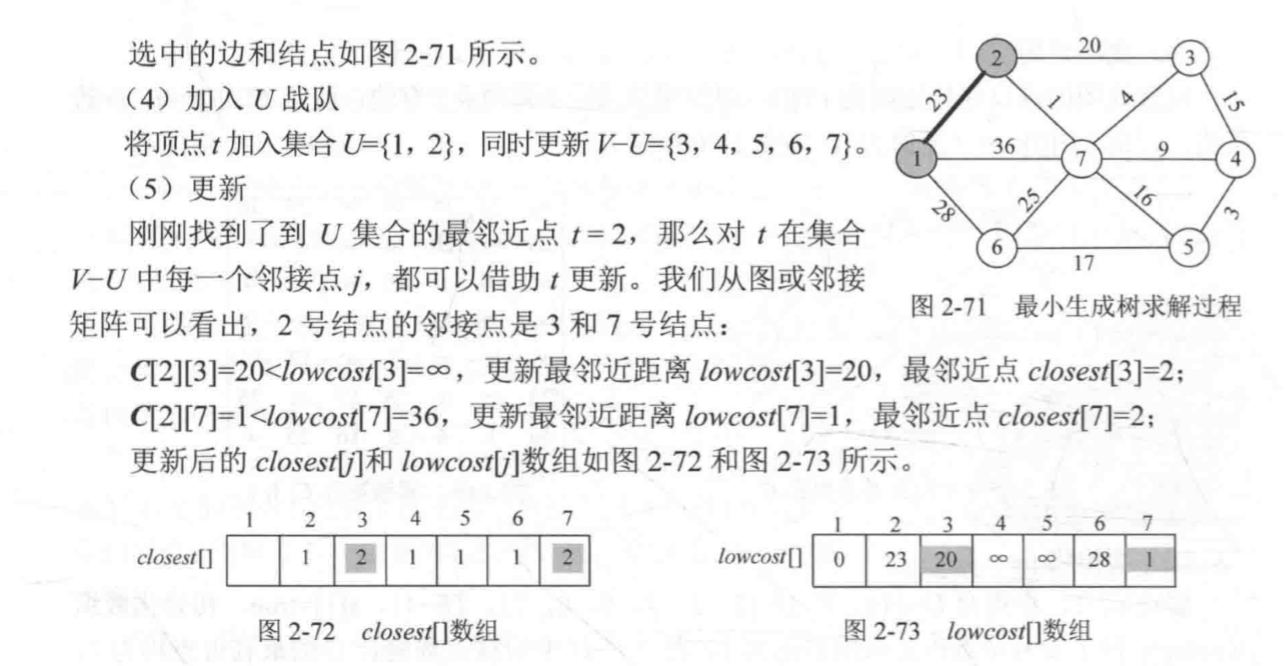
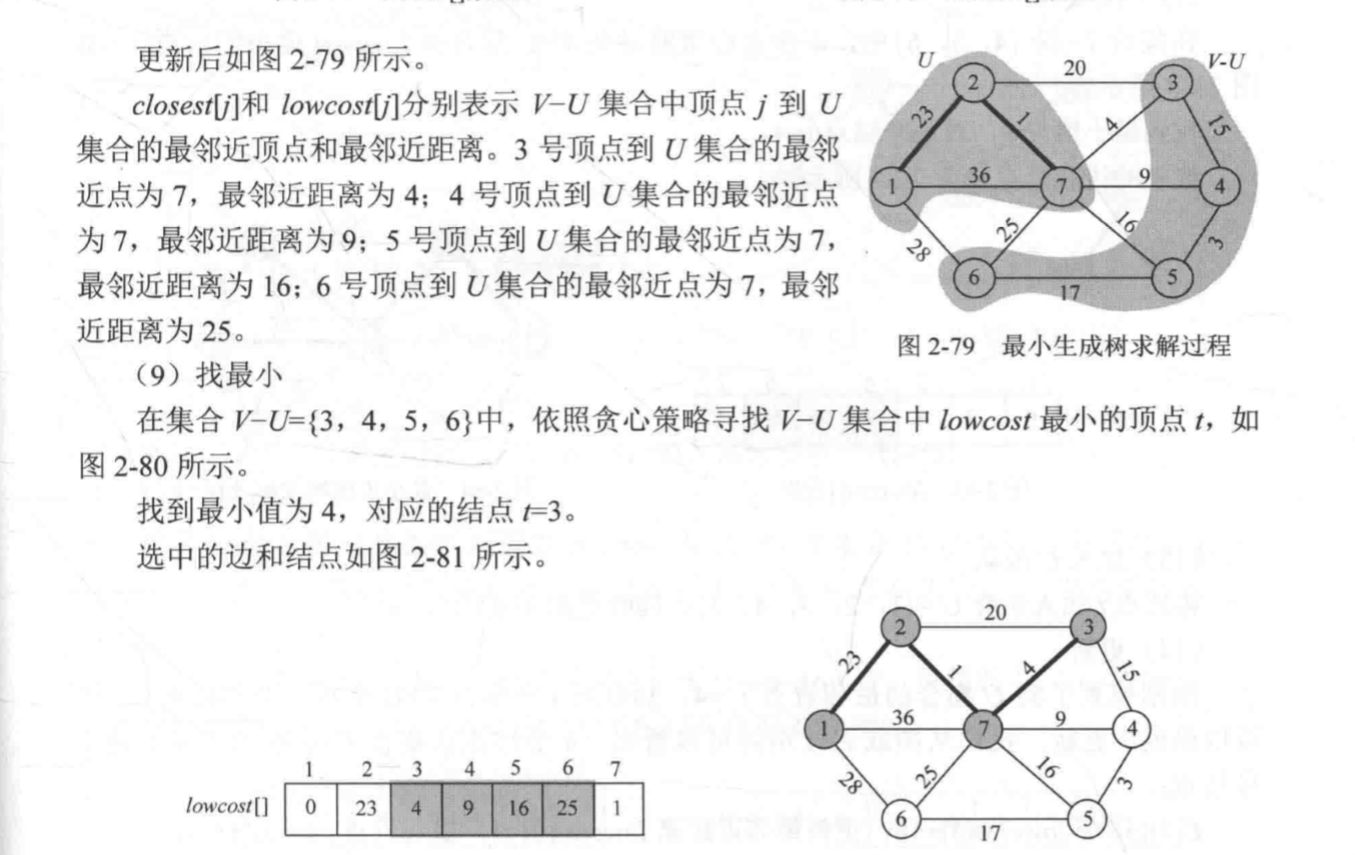
　　6：对于集合v-u中的所有顶点j，更新lowcost和closest，并转到步骤3

图解（太懒了，还是盗图来的快，哈哈哈）：

　

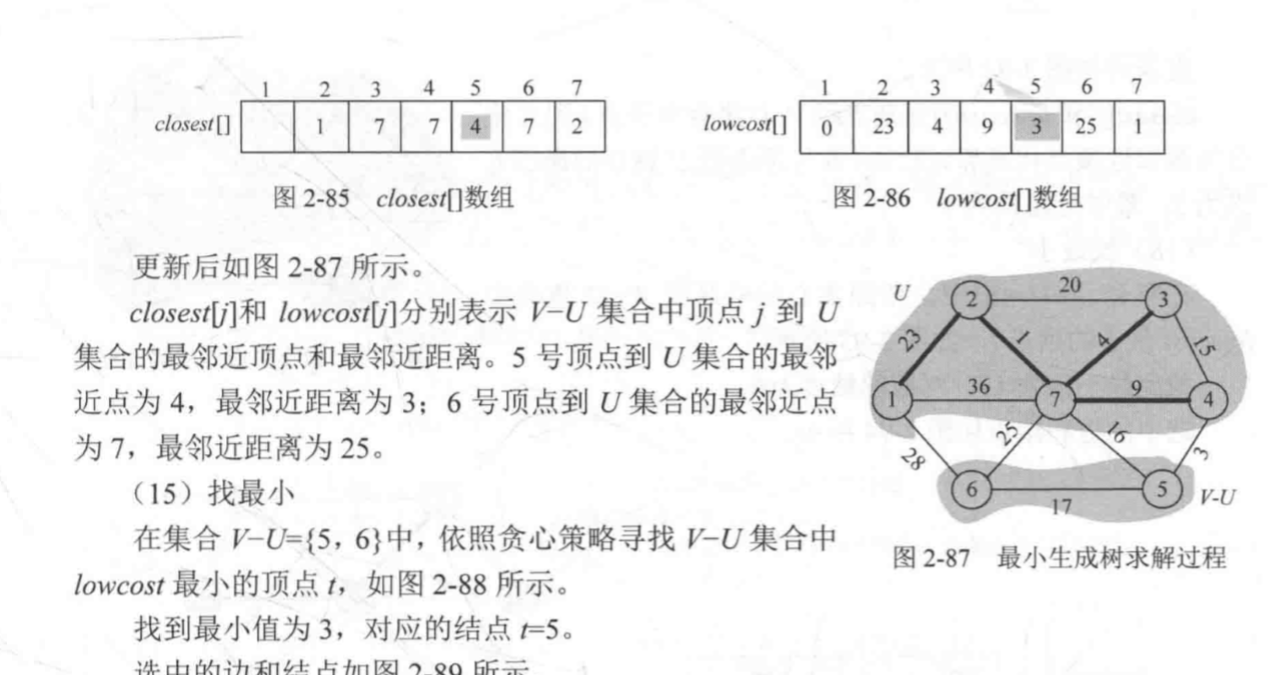
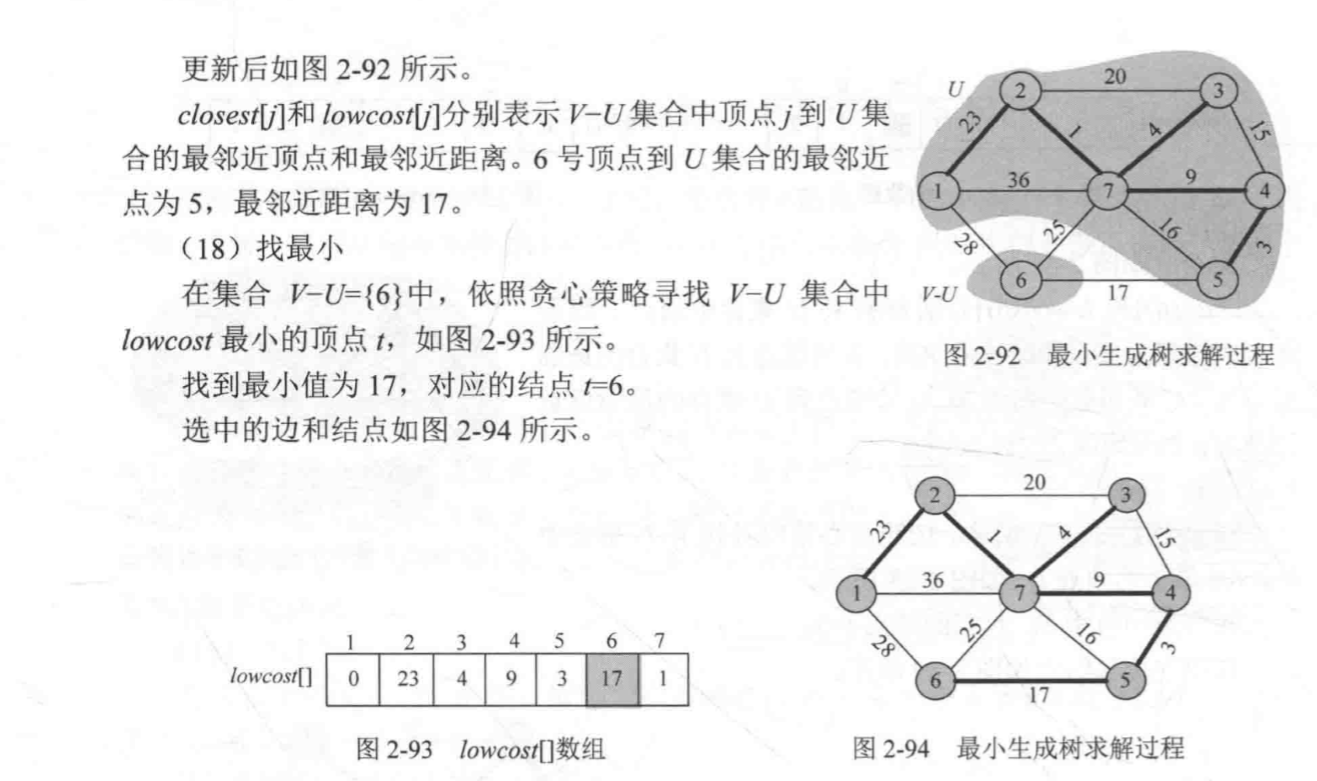
实现代码：（有点问题，过几天再改）

#include<iostream>
using namespace std;
const int INF=100000;
const int N=100;
bool s[N];
int colsest[N];
int lowcost[N];
void Prim(int n,int u,int c[N][N])
{
    int i,j;
    for(i=1;i<=n;i++)
    {
        if(i!=u)
        {
            colsest[i]=u;
            lowcost[i]=c[u][i];
            s[i]=false;
        }
        else
            lowcost[i]=0;
    }
    s[u]=true;
    for(i=1;i<=n;i++)
    {
        int temp=INF;
        int t=u;
        for(j=1;j<=n;j++)
        {
            if(!s[j]&&lowcost[j]<temp)
            {
                temp=lowcost[j];
                t=j;
            }
        }
        if(t==u)    break;
        s[t]=true;
        for(j=1;j<=n;j++)
        {
            if(!s[j]&&lowcost[j]<c[t][j])
            {
                lowcost[j]=c[t][j];
                colsest[j]=t;
            }
        }
    }
}
int main()
{
    int c[N][N];
    int n,m,u,v,w;
    int u0;
    cout<<"Please enter the number of node and edge"<<endl;
    cin>>n>>m;
    int sumcost=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            c[i][j]=INF;
    cout<<"Please enter the num of u v w"<<endl;
    for(int i=1;i<=m;i++)
    {
        cin>>u>>v>>w;
        c[u][v]=c[v][u]=w;
        
    }
    cout<<"Please enter u0 at random"<<endl;
    cin>>u0;
    Prim(n,u0,c);
    for(int i=1;i<=n;i++)
    {
        sumcost+=lowcost[i];
    }
    cout<<"The mininum of the cost"<<endl;
    cout<<sumcost<<endl;
    return 0;
}

另一种方法是利用kruskal算法，这种算法的时间复杂度当然比Prim算法低啦

首先kruskal算法用的也是一种贪心策略，不过它的实现是通过并查集啦，kruskal与prim区别

kruskal是通过找最小边，通过边联通两个分量以至于不会有环产生，而Prim是找顶点相邻的最近点

直白的说就是一个是通过边找点，另一个就是通过点找边

既然要利用并查集，那我好像还要在写一写并查集的文章了，哈哈哈，督促与激励一下自己吧

这种方法我就直接附上代码吧（步骤在注释中）

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=100;
int n,m;
int father[N];
struct Edge{
    int u,v,w;
}e[N*N];
bool cmp(Edge a,Edge b)
{
    return a.w<b.w;
}
void Init(int n)
{
    for(int i=1;i<=n;i++)
        father[i]=i;
}
int Find(int x)
{
    if(x==father[x])    return x;
    else 
    return father[x]=Find(father[x]);
}
void Merge(int a,int b)
{
    int ta=Find(a);
    int tb=Find(b);
    if(ta==tb)    return ;
    if(ta>tb)
    father[ta]=tb;
    else
    father[tb]=ta; 
}
int kruskal(int n)
{
    sort(e,e+m,cmp);
    int ans=0;
    for(int i=0;i<n;i++)
    {
        if(Merge(e[i].u,e[i].v))
        {
            ans+=e[i].w;
            n--;
            if(n==1)
            return ans;
        }
    }
    return 0;
}