递归
递归
总结:递归是一个思想,自己调用自己的一个过程
要点:
- 一定要有一个出口(结束条件)
- 写出每次重复要做的代码 包括调用自己的时机
- 递归的层级不易过多(栈溢出)
分析:
-
出口:
这个出口可以是明确的 比如说当满足特定的一个数值 如自然数的和 或阶乘中
也可以是隐藏的
- 比如递归文件操作时 file.listFiles() 的返回值 可能是 null 当为null时 也就不会在调用自身
此时是 在获得 最后一层的文件夹的 list 这时将不会在产生list 集合 递归停止(不会在调用自身)
- 比如 汉诺塔中 if(floors==1){}else{递归} 当层数为1时 就不再会取调用自身
-
调用时 是否要参数-1
这取决于你的 每次重复要做的代码是 如何书写的 如例子2 中的 实现循环功能1
其实 调用的代码也是属于 每次要重复执行的 代码
每次重复要做的代码 是不是和
for while循环体一样 所以 递归的功能 是循环
3.书写递归就是
找出什么时候不再 调用自己本身的条件 和 书写需要循环执行的代码 代码需要逻辑严密
4.注意事项
1.当两个方法相互调用时 可能出现 间接的 递归调用 可以设一个计数器来 标记调用的次数 防止栈溢出
2.递归时的判断条件 > 和>= 或需要深思熟虑 有可能平时没注意的细节 导致递归 不但预期 如二分法求元素再数组中的位置 ,当递归时 +1 -1 和判断条件是>=或结果是有区别的
- 递归的内存图和执行图
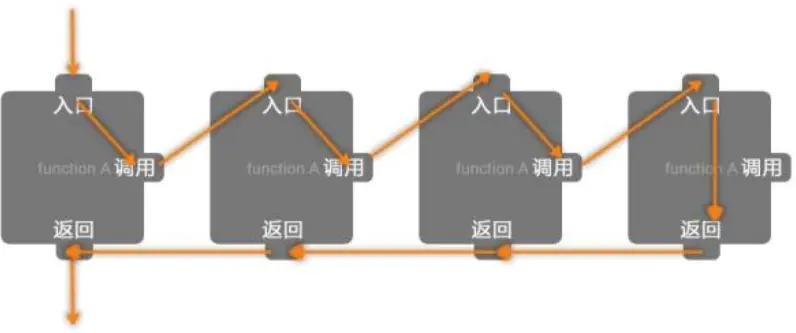
例子1-递归格式
/*
求连续自然数和 阶乘
*/
public class Recursion1 {
//递归调用
public static int sum(int num) {
if (num == 1) {
return 1;//递归出口
}
int sum =num+sum(num-1);//本次需要执行的代码
return sum;
}
//普通方法 --for循环
public static int sum1 (int num){
int sum =0;
for (int i = 1; i <= num; i++) {
sum+=i;
}
return sum;
}
public static void main(String[] args) {
System.out.println("sum(10) = " + sum(10));
System.out.println("sum1(10) = " + sum1(10));
}
}
例子2-递归功能 循环
public class One2One {
//递归-实现循环功能1
public void printNumTimes( int num){
if(num==1)return ;
System.out.println("好好学习,天天向上");
num--;
printNumTimes(num);
}
//打印1000-9999中的回文数字
//会报StackOverflowError 递归的层次太深 :感觉不是 应该是对象的引用创建的太多了
public void printNums(int num){
if (num==10000)return;
String str = num+"";
String s = new StringBuilder(str).reverse().toString();
if (str.equals(s)){
System.out.println(str);
}
printNums(num+1);
}
public static void main(String[] args) {
One2One one = new One2One();
one.printNumTimes(10);
System.out.println("----------------");
one.printNums(1000);
}
}
例子3-递归实现斐波那契数列
public class FibonacciSequence {
/*
数列: 1、1、2、3、5、8、13、21、34...
求第第12个数是多少
*/
//普通
public int method(int num_th) {
/*
想要求第12 必须知道 第11 和 第10个 ...
用变量保存 前1个 前2个 会丢失
比如说 求 第11 的时候 变量记录的值 为第10个和第9个数的值 第11个数 和第10个数 将会丢失
使用数组保存数列
*/
int [] arr = new int[num_th];
arr[0]=1;
arr[1]=1;
for (int i = 2; i < num_th; i++) {
arr[i]=arr[i-1]+arr[i-2];
}
return arr[num_th-1];
}
//递归 第n次的数量 = 第n-1次的数量+第n-2次的数量 method(int i) 就是求某次的数量
public int method2(int i){
if(i==1)return 1;
if (i==2)return 1;
return method2( i-1)+method2(i-2);
}
public static void main(String[] args) {
FibonacciSequence fq = new FibonacciSequence();
System.out.println("fq.method(12) = " + fq.method(12));
System.out.println("fq.method2(12) = " + fq.method2(12));
}
}
例子4-求文件夹中文件的全部大小
import java.io.File;
//求某个文件夹中的文件大小 (文件夹"没有大小"只是一个管理工具) 这个就没有明显的出口
public class CountFileSize {
//这个方法的功能是求文件夹中文件的大小
public int getSize(File file){
int sum=0;//记录文件中文件的大小
File[] files = file.listFiles();//获得文件夹中 所有的文件(文件和文件夹)
if (files!=null){
for (int i = 0; i < files.length; i++) {
if(files[i].isFile()){
sum+=files[i].length();//如果是文件就 累积大小
}else {
sum+=getSize(files[i]);//如果是文件夹就 就用统计好的 + 文件夹的大小
}
}
}
return sum;//最后返回统计的大小
}
public static void main(String[] args) {
File file = new File("E:\\itheima\\homework\\作业");
CountFileSize countFileSize = new CountFileSize();
System.out.println(countFileSize.getSize(file)+"b");
}
}
例子5-汉诺塔问题
//问题的描述请百度 这个原来是有明显出口的(比如if...retrun...) 后来自己改了
public class Hanoi {
int count=0;
public void innit(int floors,String A,String B ,String C){
if(floors==1){
move(floors,A ,C);
count++;
}else {
innit(floors-1,A,C,B);//这里递归调用 看参数的位置即可 实际移动的都是调用move方法
move(floors,A,C);
innit(floors-1,B,A,C);//这里递归调用 看参数的位置即可 实际移动的都是调用move方法
}
}
private void move(int floors, String A, String C) {
System.out.println("移动第"+floors+"层,从"+A +"到"+C);
}
public static void main(String[] args) {
Hanoi hanoi = new Hanoi();
long l = System.currentTimeMillis();
hanoi.innit(24,"A柱","B柱","C柱");
long l2 = System.currentTimeMillis();
System.out.println("一共移动了"+hanoi.count+"次");
System.out.println(l2-l+"ms");
}
}
例子6-二分法查找数组中是否有某个元素
//二分查找要求 数组中的元素 必须有效 升序 或 降序都可以 下面方法中的判断是基于升序数组的
public class BinarySearch {
//递归
public int binary(int findNum,int [] arr,int left,int right){
int mid=(left+right)/2;
if (left>right)return -1;//递归到了出口表示 左右 中间下标的值都不等于 查找值 没有查找到值
if(findNum>arr[mid]){
return binary(findNum,arr,mid+1,right);
}else if (findNum<arr[mid]){
return binary(findNum,arr,left,mid-1);
}else {
return mid;
}
};
//普通
public int binary2(int findNum,int [] arr,int left,int right){
while(true){
int mid=(left+right)/2;
if(findNum>arr[mid]){
left=mid+1;
}else if (findNum<arr[mid]){
right=mid+1;
}else {
return mid;
}
if(left>right){
break;
}
}
return -1;
};
public static void main(String[] args) {
//, 17, 18, 30, 39, 42, 51, 57, 58, 59, 66, 69, 69, 76, 78, 100
int [] arr = {2, 4, 6, 9, 14};
BinarySearch binarySearch =new BinarySearch();
int recursion = binarySearch.binary(15, arr, 0, arr.length - 1);
int poor = binarySearch.binary2(15, arr, 0, arr.length - 1);
System.out.println("recursion = " + recursion);
System.out.println("poor = " + poor);
}
}
例子7-快速排序
import utils.ArrOpe;
import java.util.Arrays;
public class QuickSort {
public void quick(int[] arr) {
quick0(arr, 0, arr.length-1);
}
/*
1.选取中心轴
2.右边开始找到第一个 小于中心轴的数的下标
3.左边开始找到第一个 大于中心轴的数的下标
4.如果 下标不相等 交换 第一个 左右的数 继续找第二个
下标相等 交换 较小值下标 和 基准下标
5.递归
*/
public void quick0(int[] arr, int begin, int end) {
if (begin>=end){//有可能在递归时 +1 -1 是的 begin>end
return;
}
int base = arr[begin];
int front = begin ;//front 前面 这里不能加1 对于排好序的会导致 这次front=behind=下标1 而base=下标0 if交换时 再次乱序
int behind = end;// behind 后面
while (true) {
//1.从后往前 找到第一个较小值下标
while (arr[behind] >= base && behind > front) {
behind--;
}
//2.从前往后找打第一个较大值下标
while (arr[front] <= base && behind > front) {
front++;
}
if (front != behind) {//如果 前后小标不相等 表示 这轮没有执行完 还有较小的没放左边 较大的没放右边
arr[front] = arr[front] ^ arr[behind];
arr[behind] = arr[front] ^ arr[behind];
arr[front] = arr[front] ^ arr[behind];
} else {//如果相等 表示 这轮比较完毕 把 较小值和 基准值互换位置
//细致 说是 如果是前往后 没找到较大值 此时前后下标重合 那么基准是和 这轮的某次 较小互换位置
// 如果是后往前 没找到较小值 此时前后下标重合 那么基准是和 上轮的最后一次 较小互换位置
arr[begin] = arr[front];
arr[front] = base;
break;
}
}
quick0(arr, begin, front - 1);
quick0(arr, front + 1, end);
}
public static void main(String[] args) {
QuickSort quickSort = new QuickSort();
int[] arr = ArrOpe.getArr(100, 20);
System.out.println("排序前:"+Arrays.toString(arr));
quickSort.quick(arr);
System.out.println("排序后:"+Arrays.toString(arr));
}
}
例子8-求八皇后问题--学习中
public class ...
