GCD：求2个数的最大公约数

GCD（欧几里德算法、辗转相除法）：求2个数的最大公约数

1. 举例子（转化为铺瓷砖的问题）

逻辑：每一次都用较短的部分去铺

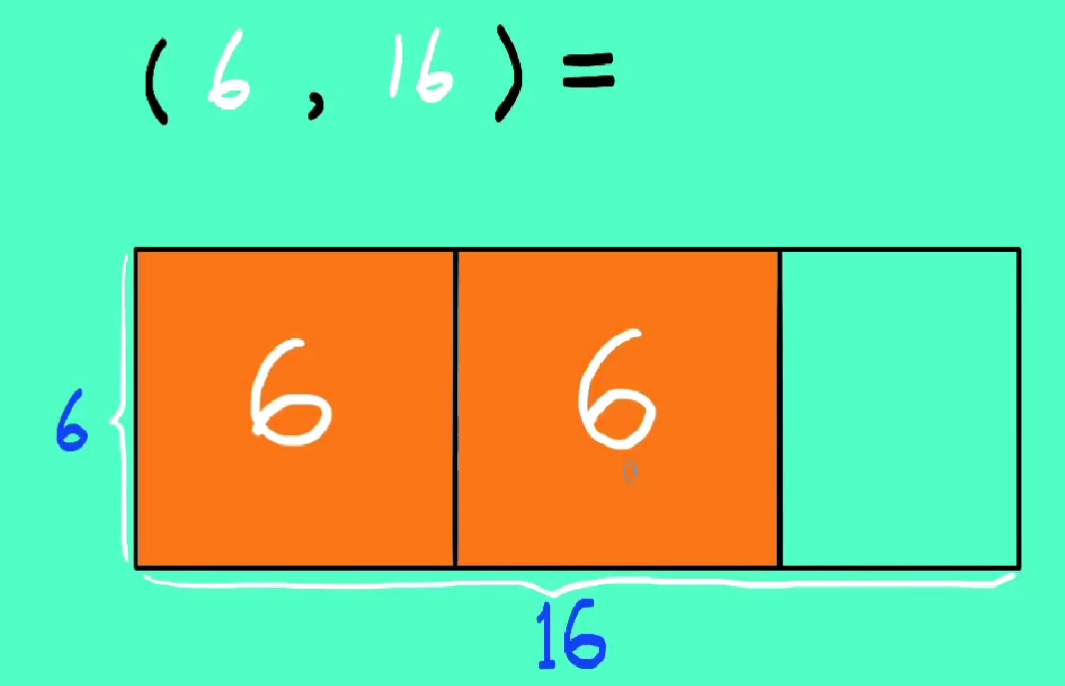
铺到最后如下：

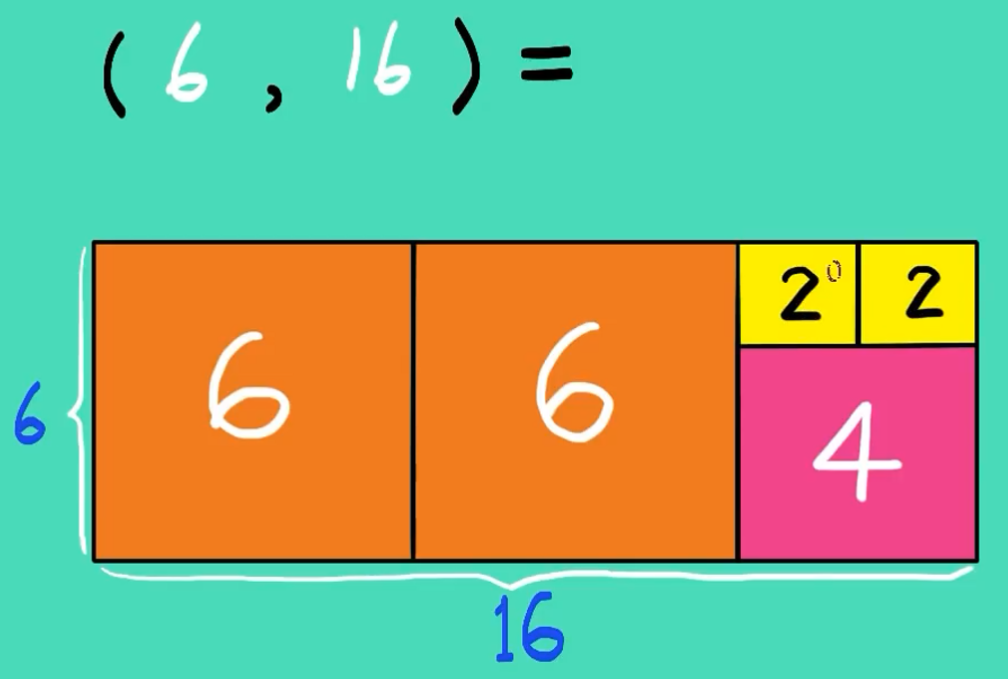
所以得到结论

2. 公式推理

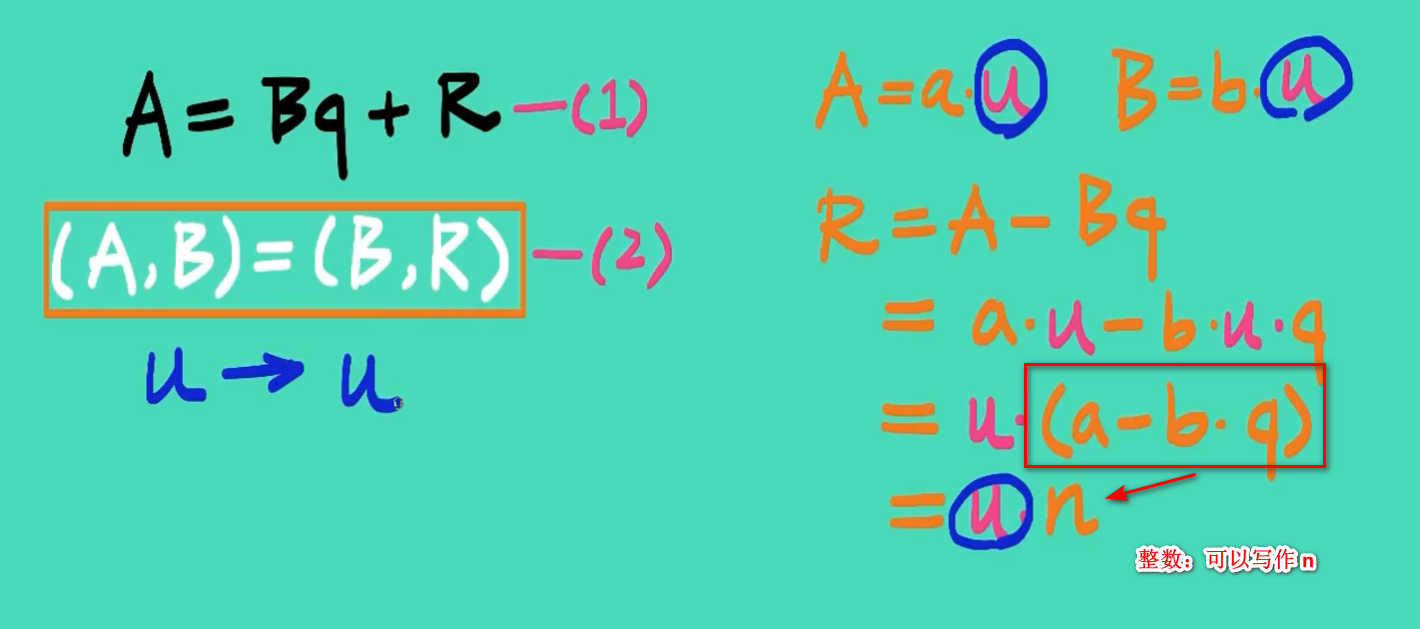
结论：
u 如果是 A 和 B 的公约数，那它必然 是 B 和 R 这 2 个数的公约数
同样反过来推理也成立

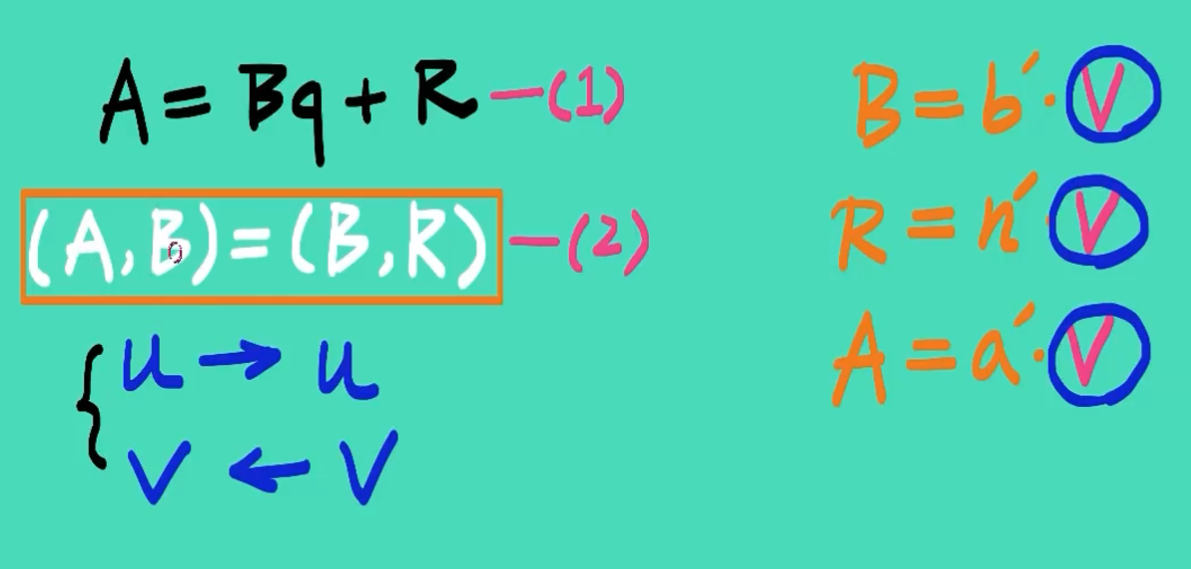
3. 代码实现

//  a：绝对值大的那个数
public int getGCD(int a, int b){
  	while (b != 0){ //【约定好除数不能为 0】
 		int temp = b; //  定义交换变量
  		b = a % b;  //  余数 R
  		a = temp;  //  除数 a 替换为 被除数 b （A，B）= （B, R）
	}
  	return a;
}

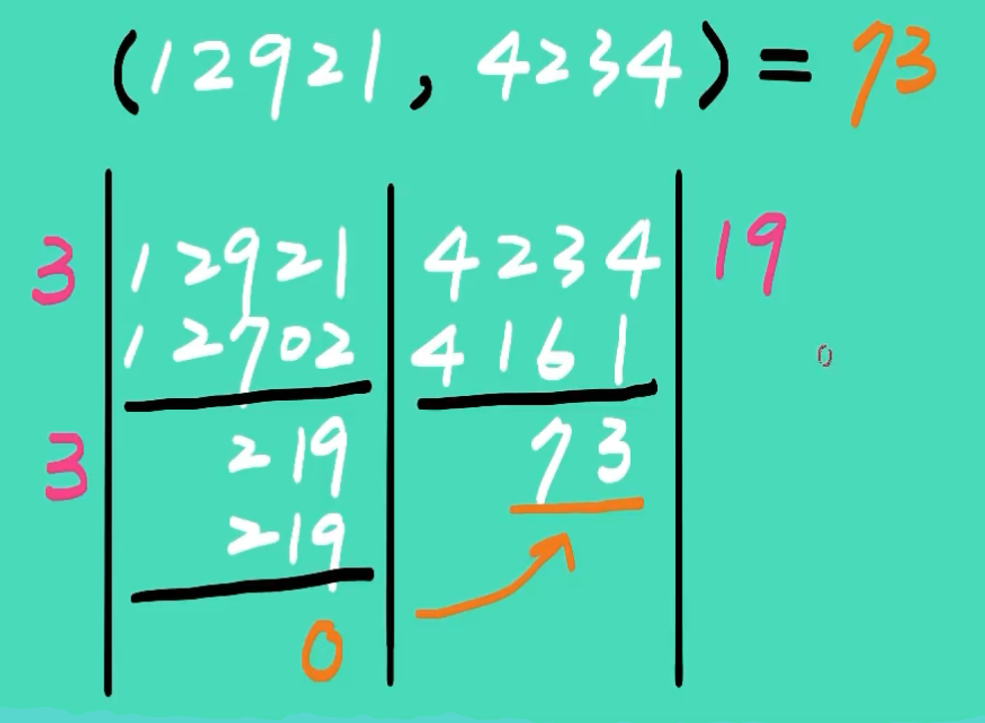
注意：余数一定小于 被除数