数论

数论

1. 数字题

注意事项：

• 0、负数、小数
• 是否需要考虑错误输入，错误输入以后应该如何处理
• 数据大小，类型范围
• int 占 4个字节，共 32位：2 ^ 32 = 4,294,967,296
• JAVA中没有无符号的数，换言之，java中的数都是有符号的
• 在计算机运算的时候，都是以 补码 的方式来运算的
• 当我们看运算结果时，要看它的原码
  Java语言中int类型的数据占4个字节，那么4个字节所能表示的最大整数是多少呢？按照补码的表示规则，这个最大的整数存储到计算机当中应该是“1个0跟31个1”： 【即：2 ^ （32 - 1）- 1 = 2147483647】
  
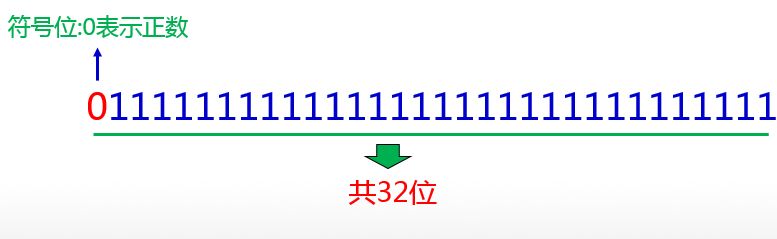
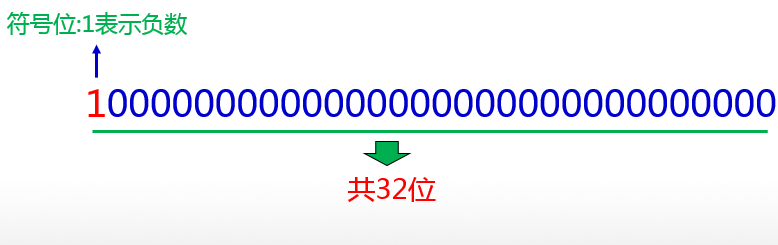
  如果我们强行给这个数再加1，按照二进制的进位规则，它会变成下面的样子： 【补码形式表示的负数】
  
  原码 = ~(反码) = ~(补码 - 1)
  补码 - 1 如下图：
  
  再取反 【表面上，这个二进制数和逆运算之前是一样的，但是它的意义已经完全不同了】
• 在进行逆运算之前，这个二进制数是一个补码形式表示的负数
• 而经过逆运算之后，这个二进制数变成了一个绝对值，既然是绝对值，它肯定不会是负数。因此，这个二进制数最前面的1并不表示负数，而是数字的一部分。
• 那么这个绝对值是多少呢？转换成十进制就是2147483648 【2 ^ (32 - 1)】。所以，我们图3中看到的那个“1开头后面跟着31个0”所表示的负数，就是-2147483648！
  

	1 1 1 1
当前位置1代表的值	2^(n - 1) 【8、4、2、1】
求和	（2 ^ n） - 1 【n：1的个数】

得出个小结论：

2 ^(n - 1)  - 【2^(n - 1)  - 1】= 1

• 当前位置代表的值 - 低位所有和 = 1
• 数据大小是否会溢出

INT_MIN 0x80000000	INT_MIN 0x80000000
-2147483648	2147483647

原码、反码、补码

Java 按位取反 ~
二进制数在内存中是以·补码 的形式存放的
符号：

• 正数：0
• 负数：1

	反码	补码
正数	\	\
负数	符号位不变，其余取反	反码 + 1

eg：

	反码	补码
9（1001）---> (0 1001)	0 1001	0 1001
-1 (0001) ---> (·1 0001)	1 1110	1 1111

因为二进制数在计算机中是以·补码 的形式存放的
求 ~9 = ?

1. 将数字9存入计算机中（以补码形式）9 ---> 0 1001
2. 进行取反 ~9 = ~(0 1001) = 1 0110 [计算机内存的数，形式位补码]
3. 现在要输出到屏幕上即（原码）

​ 原码 = ~(反码) = ~（补码 - 1） = ~(1 0110 - 1) = ~(1 0101) = 0 1010 = -10

=========================================================

求 ~5 = ?

1. 5 的 补码 = 0 0101
2. ~5 = ~(0 0101) = 1 1010 （计算机中的，形式为补码，符号位是1，代表是负数）
3. 原码 = ~(反码) = ~(补码 - 1) = ~(1 1010 - 1) = ~(1 1001) = 0 0110 = -6

==========================================================

求 ~(-2) = ?

1. -2的补码 = 1 1110
2. ~(-2) = ~(1 1110) = 0 0001 （补码状态下，现在代表一个正数）
3. 正数状态下：原码 = 补码 = 1

==========================================================

• 计算机内存只能计算 数据的补码，所以不管你想操作的是正数或者是负数，都要传入它的补码，然后进行操作
• 第二步根据符号位判断计算后的正负
  • 正数：原码 = 补码
  • 负数：原码 = ~（反码 ）= ~（补码 - 1）

浮点转 int

2.999 ---> 2
3.000 ---> 3
    
int(f + 0.000001)

Mod范围

base = 9
n % base = [0...8];	//	我们希望 [1...9]

//	更改为
(n - 1) % base + 1 = [1...9]

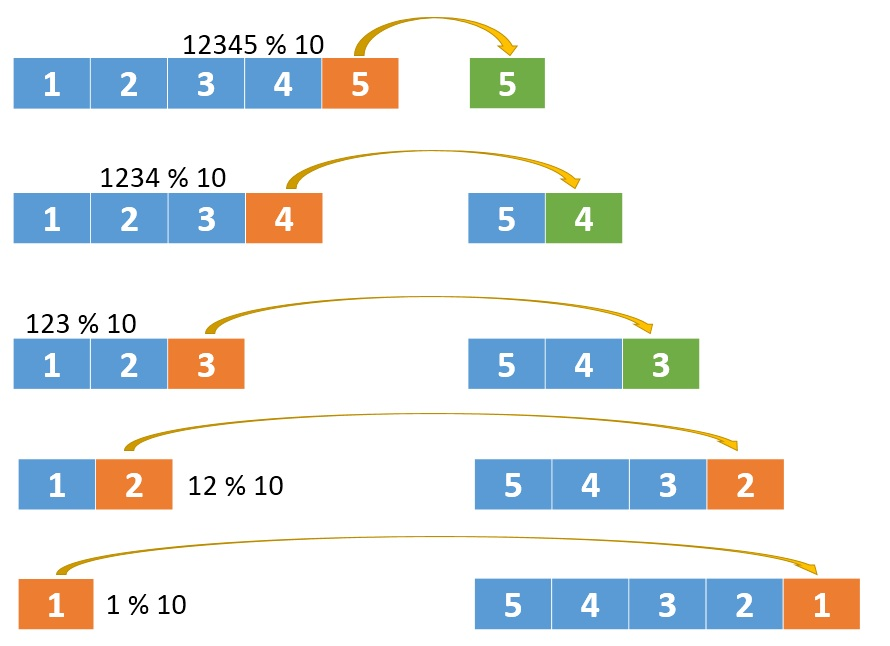
Reverse（int）

LeetCode 7 整数反转