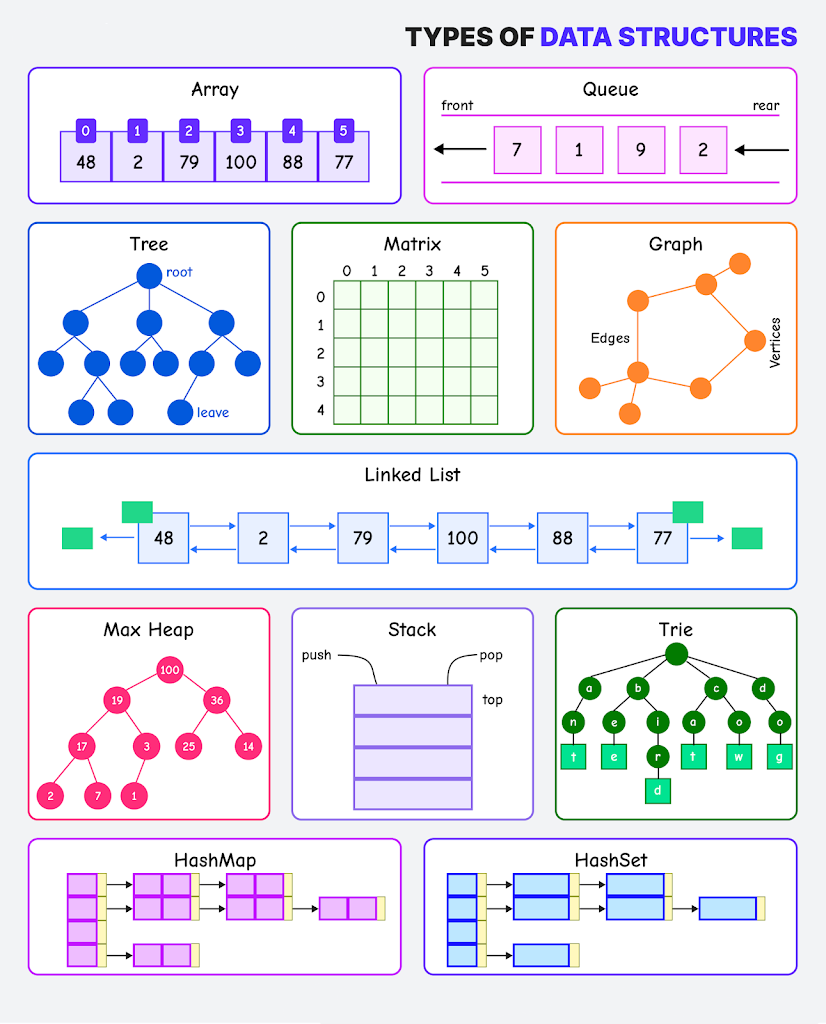
数据结构总览

数据结构总览

1. Arrays
2. Queues
3. Trees
4. Matrix / 2D Arrays
5. Graphs
6. Linked Lists
7. Heaps
8. Stack
9. Tries（前缀树）
10. HashMap
11. HashSet
    

Tries（前缀树、字典树）

定义【信息复用】

前缀树又称字典树，英文名：Trie：
每个样本，都是从头节点开始，根据前缀字符或者前缀数字 建出来的一棵大树，就是前缀树
没有路就新建节点，没有的话，就复用节点

• 使用场景：需要根据前缀信息来查询的场景
• 优点：根据前缀信息选择树上的分支，可以节省大量的时间
• 缺点：比较浪费空间，和总字符数量有关，字符的种类有关
• 定制：pass、end等信息

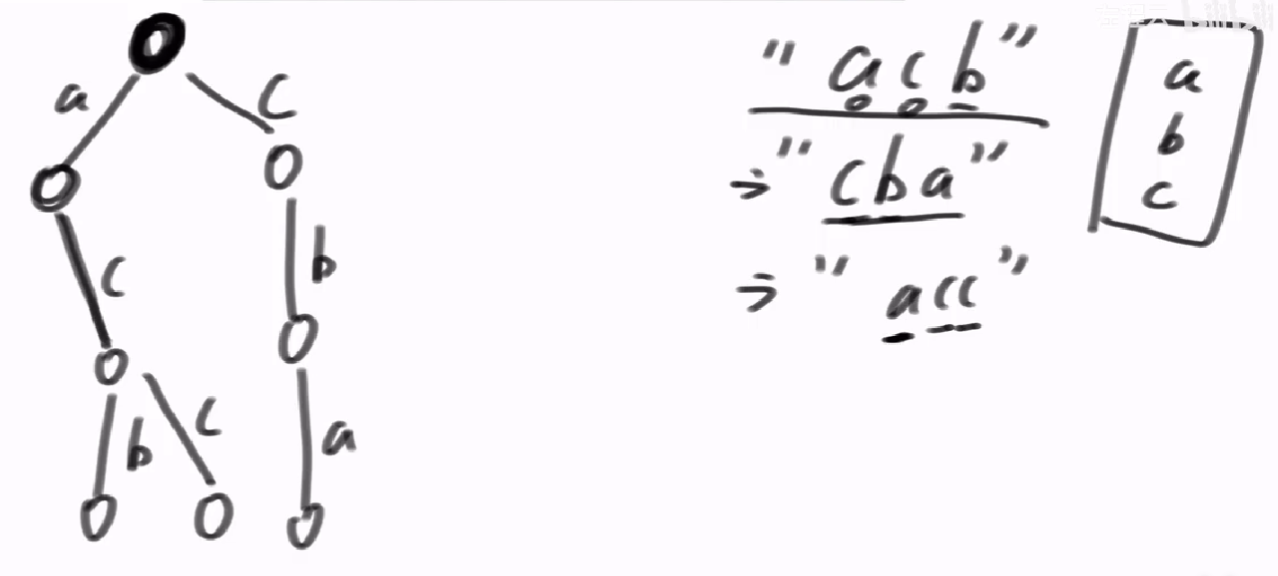
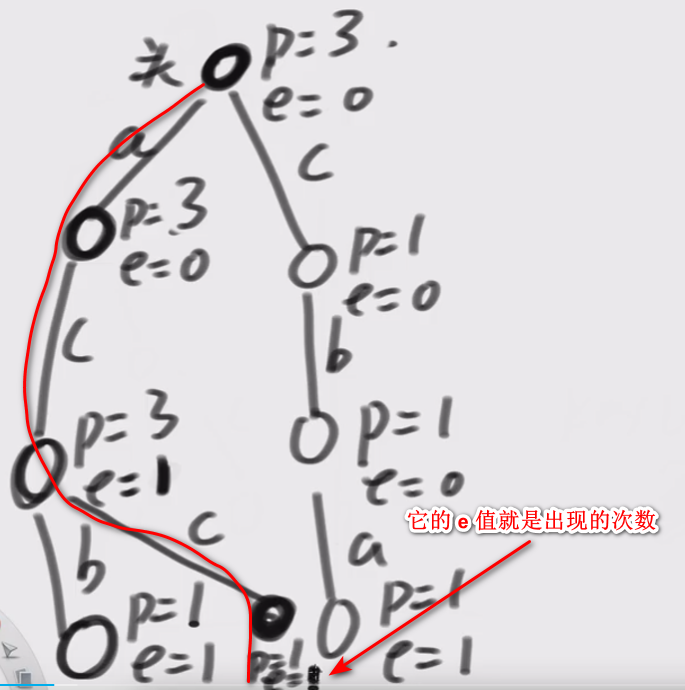
现在：假设节点上带有信息（pass：路过几次、end：以当前节点结尾）

那么根据上述信息我们可以得出许多结论：

1. acc 出现了几次
   
2. 一共添加过多少个字符串
   
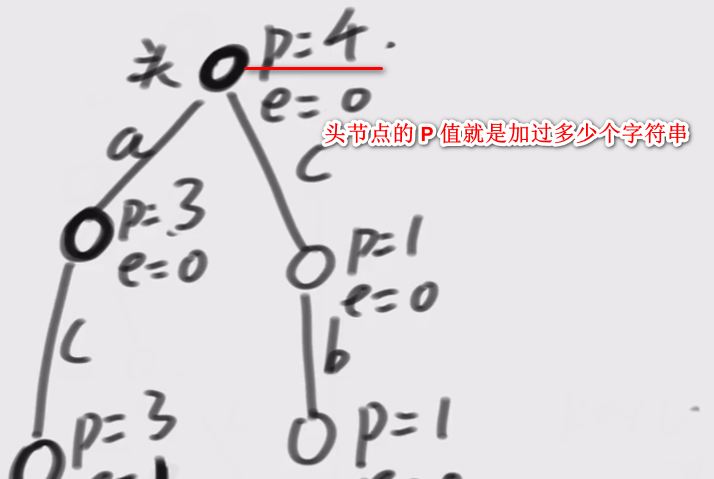
3. 以 ac 为开头
   
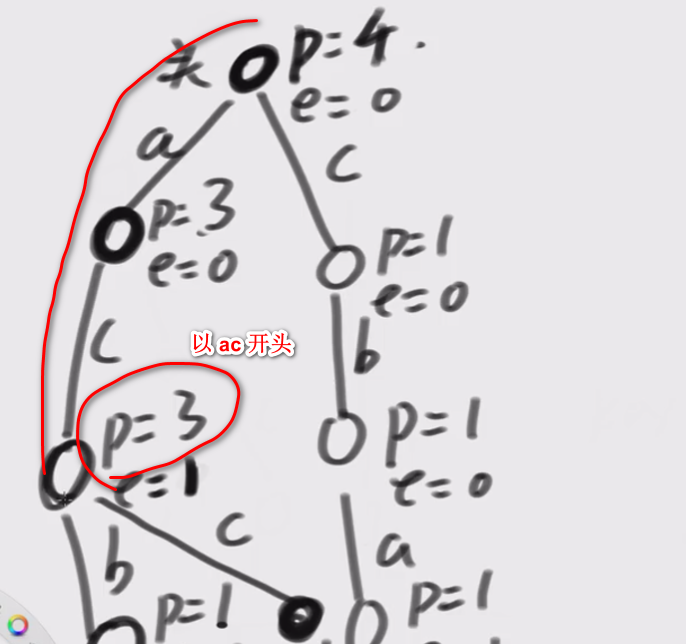
4. 以 ab 为开头
   0个

实现方式

1. 类描述的实现方式【动态结构】

1. 路的可能性范围较小，用 固定数组 实现路）（LeetCode208：实现 Trie）

class Trie {

    TrieNode root;

    public Trie() { //  前缀树初始化 ===> 建立头节点
        root = new TrieNode();
    }
    
    public void insert(String word) {
        TrieNode dummy = root;  //  定义指针
        dummy.pass++;
        for (char c : word.toCharArray()) { //  遍历字
            int path = c - 'a';
            if (dummy.next[path] == null){
                dummy.next[path] = new TrieNode();
            }
            dummy = dummy.next[path];
            dummy.pass++;
        }
        dummy.end++;    //  结尾 end++
    }
    
    public boolean search(String word) {
        TrieNode dummy = root;
        for (char c : word.toCharArray()) {
            int path = c - 'a';
            if (dummy.next[path] == null){
                return false;
            }
            dummy = dummy.next[path];
        }
        return dummy.end > 0;
    }
    
    public boolean startsWith(String prefix) {
        TrieNode dummy = root;
        for (char c : prefix.toCharArray()) {
            int path = c - 'a';
            if (dummy.next[path] == null){
                return false;
            }
            dummy = dummy.next[path];
        }
        return true;
    }

}

class TrieNode{
    int pass;
    int end;
    TrieNode[] next;

    public TrieNode() {
        next = new TrieNode[26];
    }
}


/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

删除：

• 如果之前 word 插入过 前缀树，那么删掉一次
• 如果之前 word 没有插入过 前缀树，那么什么也不做
  
  
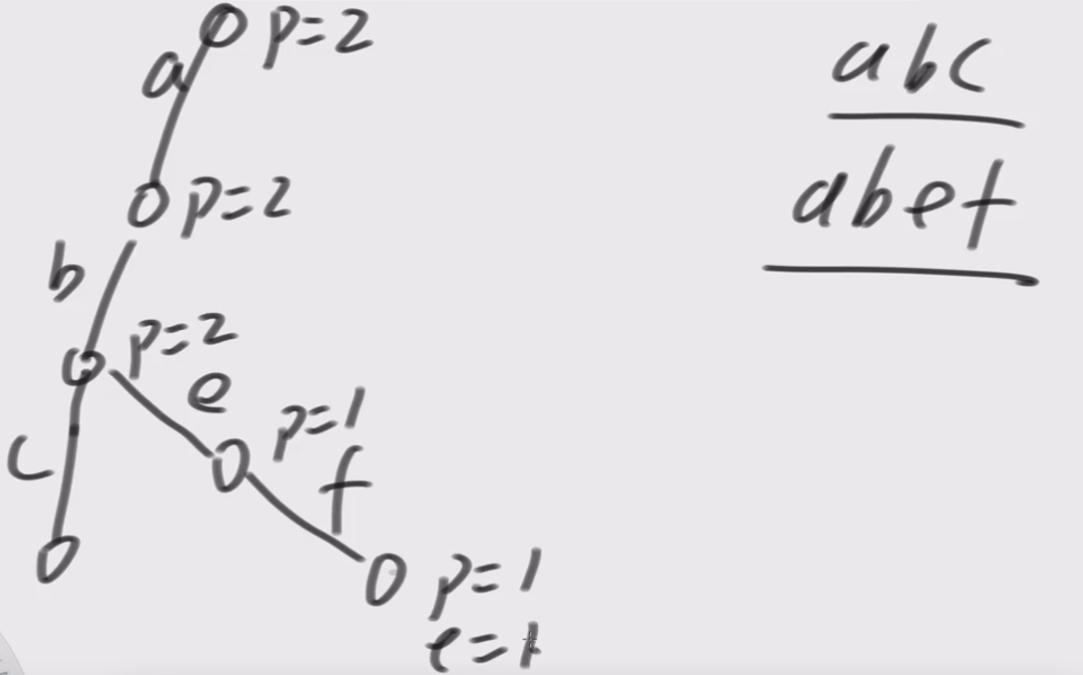
  举例子：
  
  
  
  
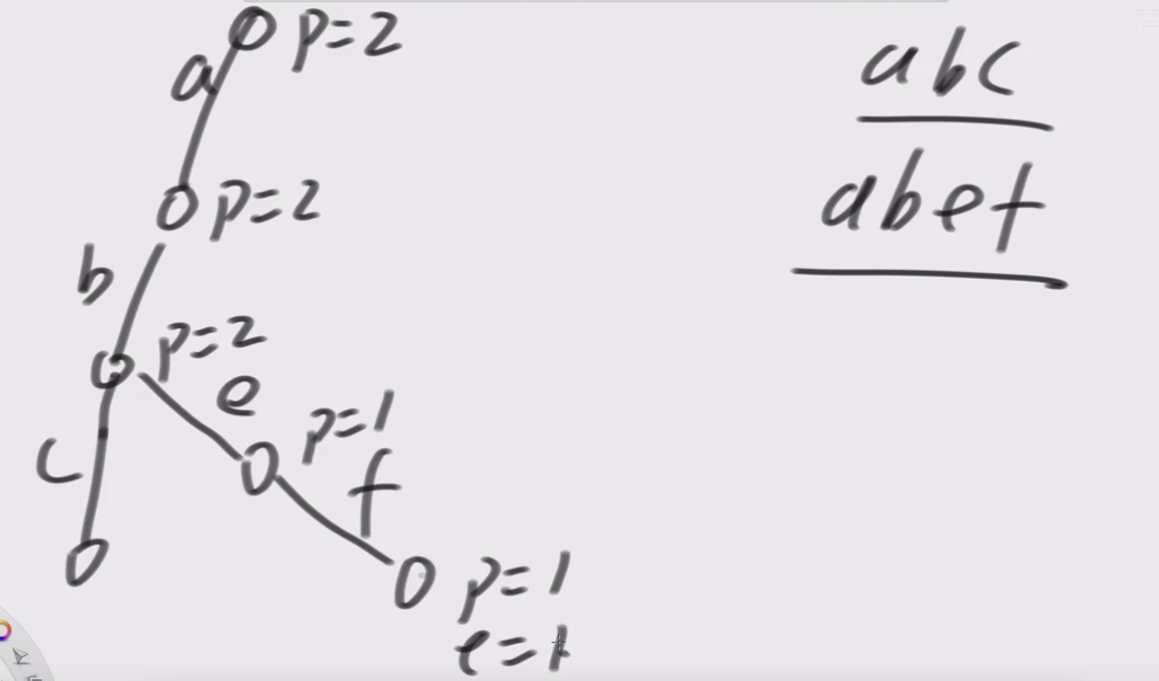
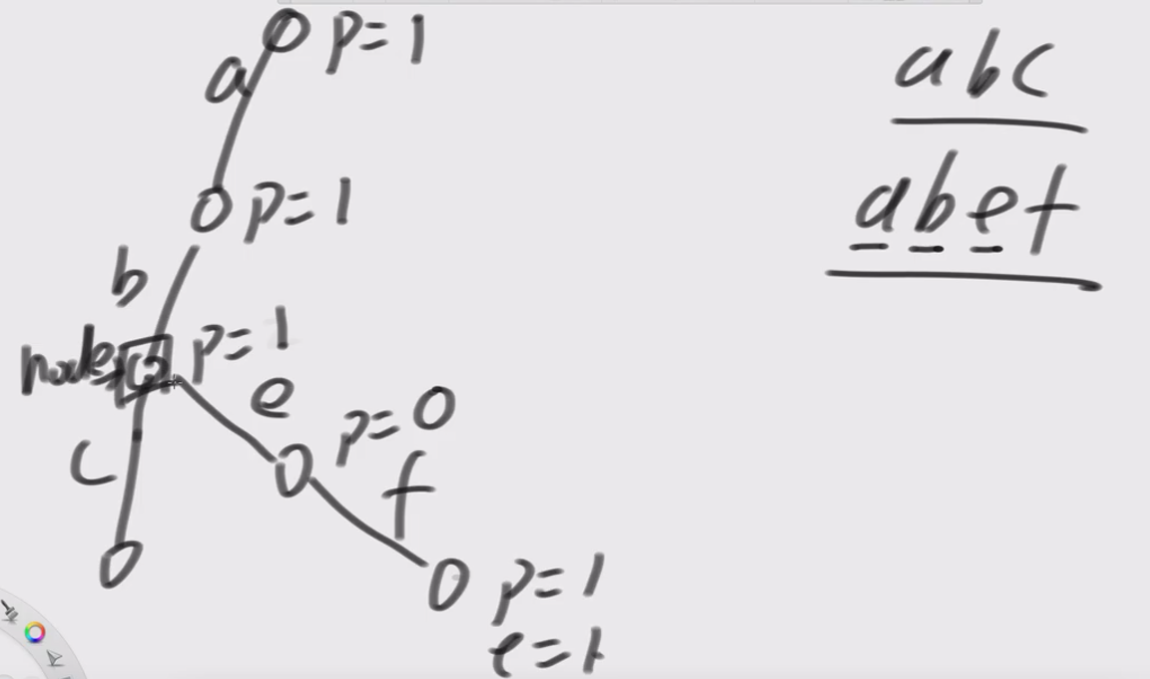
  最后一个节点 end --

2. 路的可能性范围较大，用 哈希表 实现路

65535 条路，如果是数组的话，太浪费空间了 ===> 莫不如改成一个 map了

• key：路
• value：下级节点地址

class TrieNode{
    int pass;
    int end;
    Map<Integer, TrieNode> next;

    public TrieNode() {
        next = new HashMap<>();
    }
}

2. 静态数组的实现方式【推荐】

1. 一切都是静态数组来实现，提交准备好够用的空间
2. 如果路的可能性范围较大，就用每一位的信息建树