单源最短路径问题【Dijistra】
单源最短路径问题
无向图【可以转化为BFS:无权(或者边界权相等)图的最短路径】
首先先构造邻接表
特殊情况如下:
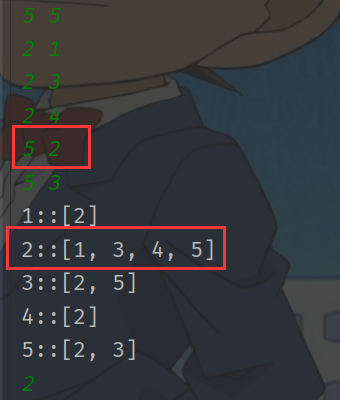
# 由于是无向图:我们最后要从 2 出发开始扩散
如果不考虑2次的话,就得不到下面的邻接表了,因为是无向图,那么 5 2 也是 2 5,所以我们利用 hashSet来进行操作
5 5
2 1
2 3
2 4
5 2
5 3
2
import java.util.Scanner;
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
static Map<Integer, Set<Integer>> map = new HashMap<>(); // 邻接表
static Deque<Integer> deque = new ArrayDeque<>();
static boolean[] isVisited;
static int res = 0;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int count = in.nextInt(); // 点个数
isVisited = new boolean[count + 1];
int row = in.nextInt();
for (int i = 0; i < row; i++) {
int a = in.nextInt();
int b = in.nextInt();
Set<Integer> orDefault1 = map.getOrDefault(a, new HashSet<>());
orDefault1.add(b);
Set<Integer> orDefault2 = map.getOrDefault(b, new HashSet<>());
orDefault2.add(a);
map.put(a, orDefault1);
map.put(b, orDefault2);
}
int start = in.nextInt();
deque.offer(start); // 将 2 压入队列
isVisited[start] = true;
bfs();
System.out.println((res - 1) * 2); // 经过多少天可以辐射全部!!!【减去初始的那天!!!】
}
public static void bfs(){
while (!deque.isEmpty()){
int len = deque.size();
while (len > 0){
Integer peek = deque.pop();
if (map.containsKey(peek)){
Set<Integer> set = map.get(peek);
for (Integer integer : set) {
if (!isVisited[integer]){
deque.offer(integer);
isVisited[integer] = true;
}
}
}
len--;
}
res++;
}
}
}
有向图
【Dijistra】:无负权边的单源最短路 ===> 优点队列 堆优化
基于顶点求单源最短路的方法
n 个顶点,m条边 ===> 算法时间复杂度为:\(o(n^2)\)
适合点少、边多的稠密图
实现步骤:
- 设一个集合 T,保存已经找到的最短路的顶点,先将起点加入集合
- 将起点到所有点的距离存在 dis 数组中,不能直接到达的点存为 INF
- 在 dis 数组中找 min、当前值一定是起点到该店的最短路,将该点加入集合
- 遍历其它的点:如果它们通过这个最短的点作为中转,比源点直接到达短,就替换这些顶点到源点的 dis 值(松弛 操作)
if (dis[i] > dis[min] + map[min, i]){
dis[i] = dis[min] + map[min, i];
}
- 又从 dis 中找出最小值,重复上面的操作,直至 T 集合包含所有顶点
743. 网络延迟时间
class Solution {
int INF = 600001;
boolean[] isVisited;
int[][] arr;
public int networkDelayTime(int[][] times, int n, int k) {
int[] dis = new int[n + 1];
isVisited = new boolean[n + 1];
arr = new int[n + 1][n + 1];
for (int i = 0; i < arr.length; i++) {
Arrays.fill(arr[i], INF);
}
for (int[] time : times) {
arr[time[0]][time[1]] = time[2];
}
Dijistra(dis, n, k);
int res = Integer.MIN_VALUE;
for (int i = 1; i <= n; i++) {
if (dis[i] == INF){ // 有不可达的!!!
return -1;
}
res = Math.max(res, dis[i]);
}
return res;
}
public void Dijistra(int[] dis, int n, int k){
Arrays.fill(dis, INF);
dis[k] = 0; // 只有 start的距离是 0
for (int i = 1; i <= n; i++) { // 遍历 n 次
int min = INF;
int index = -1;
for (int j = 1; j <= n; j++) { // 在未访问过的里面找出距离最小的
if (!isVisited[j] && dis[j] < min){
min = dis[j];
index = j;
}
}
if (index == -1){ // 剩下的都是不可达的点了,也就无须更新了
return;
}
isVisited[index] = true;
for (int j = 1; j <= n; j++) { // 利用这个最小值去松弛
if (dis[j] > min + arr[index][j]){
dis[j] = min + arr[index][j];
}
}
}
}
}
最小传输时延Ⅱ【注意最大值:INF = Integer.MAX_VALUE / 2】
思路:
- 构建邻接矩阵【利用 getReach 方法:如果和目的地大小一致且大于0,时延 - 1】
- Dijistra算法【传入 dis[] 数组】
- 最终结果 = dis[dis.length - 1] + arr[row - 1][col - 1];
import java.util.Scanner;
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
static boolean[] isVisited;
static int[][] canReach;
static int[][] offsets = {{0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1}, {-1, 0}, {-1, 1}};
static int row;
static int col;
static int INF = Integer.MAX_VALUE / 2;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
row = in.nextInt();
col = in.nextInt();
int[][] arr = new int[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
arr[i][j] = in.nextInt();
}
}
canReach = new int[row * col][row * col];
for (int i = 0; i < canReach.length; i++) {
Arrays.fill(canReach[i], INF);
}
int[] dis = new int[row * col];
isVisited = new boolean[row * col];
getReach(arr);
Dijistra(dis);
System.out.println(dis[dis.length - 1] + arr[row - 1][col - 1]);
}
public static void Dijistra(int[] dis) {
Arrays.fill(dis, INF);
dis[0] = 0; // 起点设为 0
for (int i = 0; i < dis.length; i++) {
int index = -1;
int min = INF;
for (int j = 0; j < dis.length; j++) {
if (!isVisited[j] && dis[j] < min) {
min = dis[j];
index = j;
}
}
if (index == -1) { // 能够找到最小值下标
return;
}
isVisited[index] = true; // 标记
// 松弛
for (int k = 0; k < dis.length; k++) {
dis[k] = Math.min(dis[k], min + canReach[index][k]);
}
}
}
public static void getReach(int[][] arr){
// 按照 id 进行标记:i * col + j
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
int now = arr[i][j];
for (int[] offset : offsets) {
int x = i + offset[0];
int y = j + offset[1];
if (x >= 0 && x < row && y >= 0 && y < col){
int other = arr[x][y];
if (now == other && now != 0){
canReach[i * col + j][x * col + y] = now - 1;
}else {
canReach[i * col + j][x * col + y] = now;
}
}
}
}
}
}
}
【bellman-ford】:可以求带负权边的图的单源最短路并且可以判断图是否存在负环(因为路径权会无线缩小)===> 队列优化 SPFA
【floyd】:可以求带负权边,但不带负环图的多源最短路
多源最短路:整个图的每个点到其它所有点的最短路


 浙公网安备 33010602011771号
浙公网安备 33010602011771号