数字问题:位运算
数学问题
224. 工号不够用怎么办
这里说人数 0< X <=2^50 – 1,由于 long类型可以表示 64 位,可以使用 long 数据类型来表示2的50次方
import java.util.Scanner;
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
// 由小写英文字母(a-z)和数字(0-9)两部分
// 新工号由一段英文字母开头,之后跟随一段数字,比如”aaahw0001″,”a12345″,”abcd1″,”a00″。
// 新工号不能全为字母或者数字,允许数字部分有前导0或者全为0
Scanner in = new Scanner(System.in);
String[] split = in.nextLine().split(" ");
long X = Long.parseLong(split[0]); // 人数 0< X <=2^50 – 1
int Y = Integer.parseInt(split[1]) ; // 新工号中字母的长度Y 0< Y <=5 【26】
// 公式:X = 26 ^ Y * 10 ^ Z
long res = (long)Math.ceil(Math.log10(X / Math.pow(26, Y)));
if (res == 0){
System.out.println(1);
return;
}
System.out.println(res);
}
}
二进制和位运算
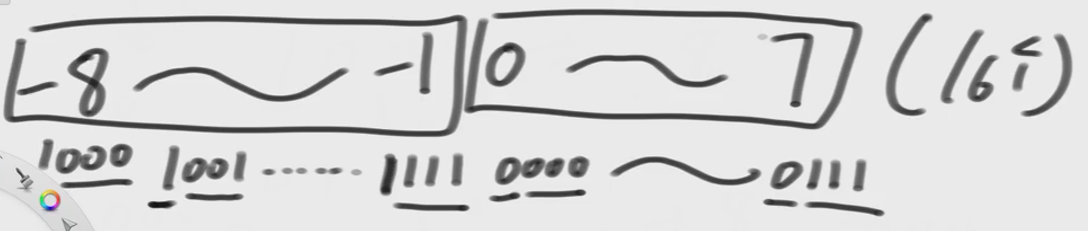
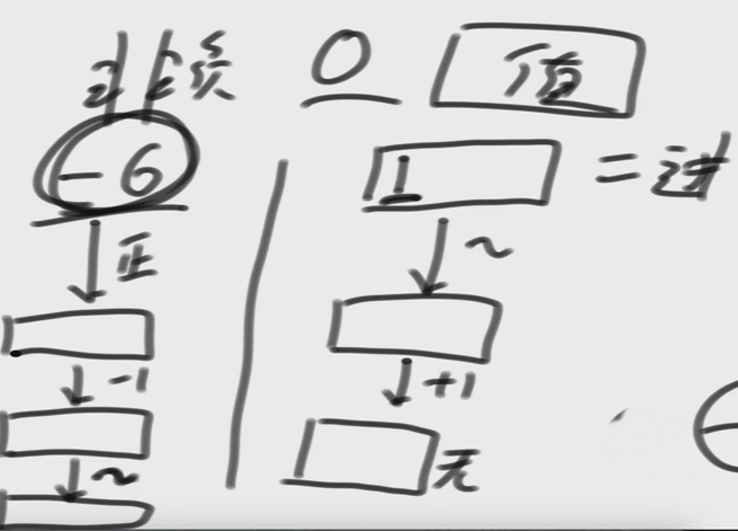
负数【十进制】===> 二进制
- 转成正数
- -1
- ~:取反
# 将 -1 转成二进制
-1
正数为:1【0001】
减 1:0000
最后取反: 1111
# 将 -2 转成二进制
-2
正数为:2【0010】
减 1:0001
最后取反:1110
# 将 -7 转成二进制
正数为:7【0111】
减 1:0110
最后取反:1001
# 将 - 8 转成二进制
正数为:8【1000】
减 1:0111
最后取反:1000
已知二进制是负数 ===> 对应的十进制
- 取反
- 加一
- 加上负号
# 1001 对应的负数
取反:0110
加一:0111【7】
加上负号:-7
右移


打印一个 int 类型的数字,32进制的状态
public static void printBinary(int num){
for (int i = 31; i >= 0; i--) {
System.out.print((num & (1 << i)) == 0?"0":"1");
}
}
如果是 Long 类型的,要将1转换成 Long类型的,即:1L
位运算实现 +-*/
+
我们的异或是无进位相加!!!
a+b = a^b + 进位信息 # 当进位信息消失的时候,这个就是正确的

public static int add(int a, int b){
int res = a;
while (b != 0){
res = a ^ b; // 无进位相加的和
b = (a & b) << 1; // 进位信息
a= res;
}
return res;
}
-
a - b = a + (-b)
public static int minus(int a, int b){
int fuB = add(~b, 1);
return add(a, fuB);
}
*
/
相关代码:
public class oop {
public static void main(String[] args) {
System.out.println(add(100, 2));
System.out.println(minus(100, 2));
printBinary(1);
System.out.println();
System.out.println("============");
int c = 0b1001110;
System.out.println(c);
// 取得自己的相反数:取反 + 1
System.out.println(~c + 1);
// 特殊情况:负数的最小值利用上面的公式取不到相反数
System.out.print(Integer.MIN_VALUE); // -2147483648
System.out.println(~Integer.MIN_VALUE + 1); // -2147483648【发现还是自己】
System.out.println((long)~Integer.MIN_VALUE + 1); // 2147483648 (可以转成 long 来规避)
int d = 0x4e;
System.out.println(d);
}
public static void printBinary(int num){
for (int i = 31; i >= 0; i--) {
System.out.print((num & (1 << i)) == 0?"0":"1");
}
}
public static int add(int a, int b){
int res = a;
while (b != 0){
res = a ^ b; // 无进位相加的和
b = (a & b) << 1; // 进位信息
a= res;
}
return res;
}
public static int minus(int a, int b){
int fuB = add(~b, 1);
return add(a, fuB);
}
}
OD:123 分积木
分析:
我们想按Koko的求和逻辑平分总重量的话,必然要生成两份相同的二进制数重量,而两个相同二进制数按位异或的结果就是0
System.out.println(1^2^3);
System.out.println(1^2); // 3
System.out.println(1^3); // 2
System.out.println(2^3); // 1
条件:异或和 = 0,就说明:
任何数 = 剩余数的异或和
那么:我们想要异或和中的实际和最大的话,就把最小的那个数字甩走就好了!!!
import java.util.Scanner;
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int count = Integer.parseInt(in.nextLine());
String[] split = in.nextLine().split(" ");
int[] arr = new int[count];
for (int i = 0; i < arr.length; i++) {
arr[i] = Integer.parseInt(split[i]);
}
Arrays.sort(arr);
int min = arr[0];
int total = arr[0];
int specialTotal = arr[0];
for (int i = 1; i < count; i++) {
total += arr[i];
specialTotal ^= arr[i];
}
if (specialTotal != 0){
System.out.println("NO");
return;
}
System.out.println(total - min);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号