图
图
连通图：
常用概念：
- 顶点：vetex
- 边：edge
- 路径
- 无向图
- 有向图
- 带权图
1. 图的性质
边的个数：
- 有向图：\(0\leq count\leq \frac{1}{2}n(n-1)\)【每个顶点至多可以发出 n - 1条边，共n 个顶点，所以至多有 n(n - 1)条边】
- 无向图：\(0\leq count\leq n(n-1)\)
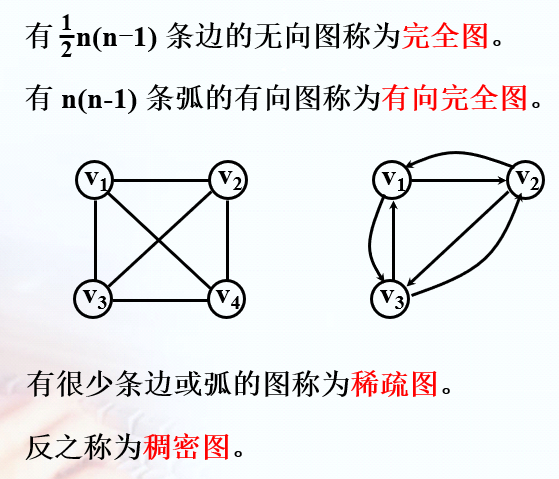
完全图、稀疏图、稠密图
邻接和关联
邻接：v 和 v' 相邻接
关联：边(v, v')与顶点 v，v' 相关联
顶点的度
无向图：顶点的度是与该顶点相关联的边的数目
有向图：分为入度和出度
性质：对于一个图（有向、无向）
边的个数 = （所有顶点的度和）/ 2
无向图
连通图【一个顶点不必与另一个顶点直接相连，可以通过其它顶点到达即可】
无向图中，任意两个顶点是连通的：最少有 n - 1 条边
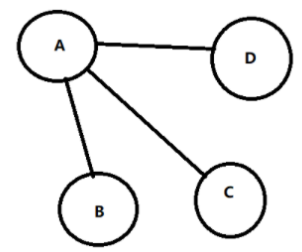
- 例如：4个点最少需要 3 条边才能连通
- 如下图：B 可以通过 A 连接到 C
非连通图
由多个互不相连的连通分量组成的无向图
- 边数少于 n - 1 条
- 最多有 \((n-1)*(n-2)/2\)条边
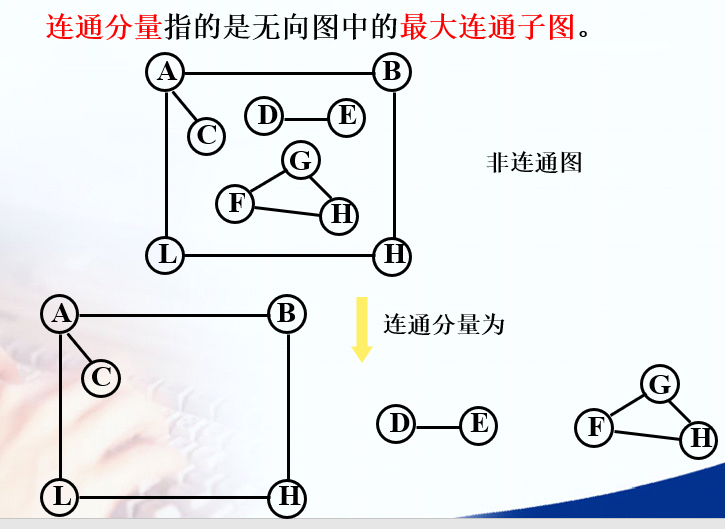
连通分量
有向图
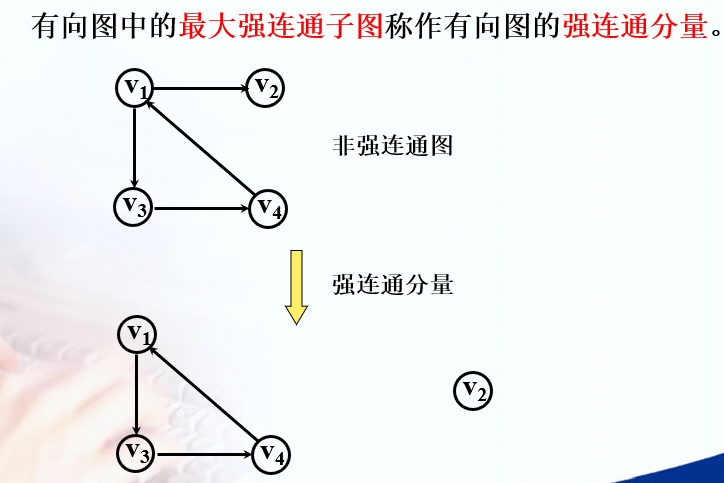
强连通图
强连通图：从a到b和从b到a都有路径。最少有n条边，假若少了A-D的路径，则A可以到D，但是D到不了A，就不满足条件。
强连通分量
生成树
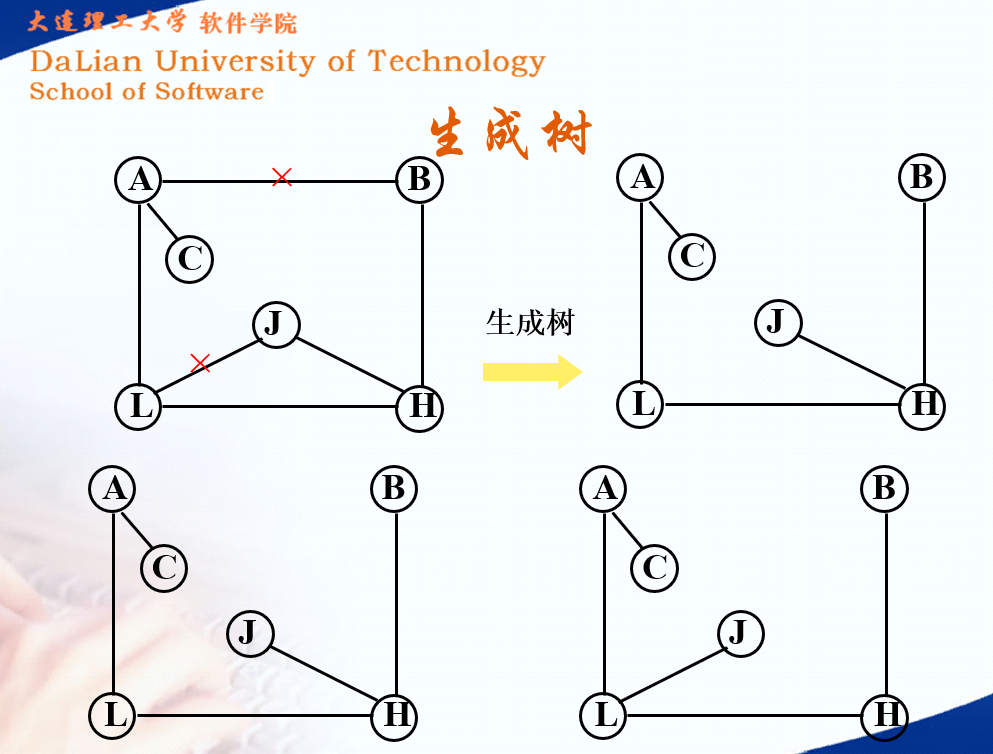
生成树的性质：
2. 图的表示方式
二维数组【邻接矩阵】
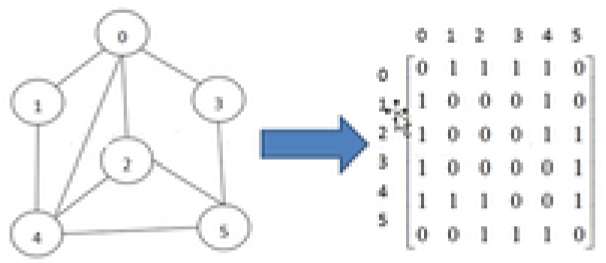
链表【邻接表】：数组 + 链表
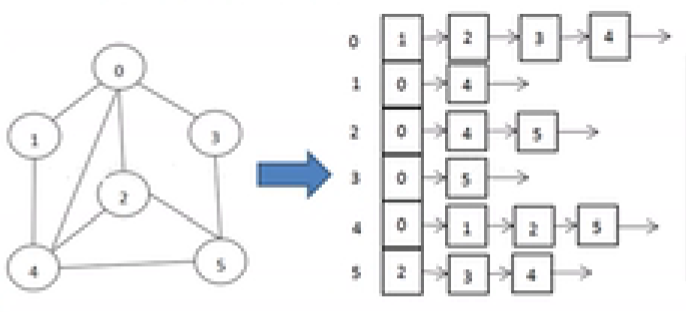
3. 简易无向图实现
package graph;
public class Graph {
private ArrayList<String> vertexList = new ArrayList<>(); // 点
private int[][] edges; // 边
private int numOfEdges; // 边的数目
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.insertVertx("A");
graph.insertVertx("B");
graph.insertVertx("C");
graph.insertEdge("A", "B", 2);
graph.printArr();
System.out.println("顶点个数 " + graph.getNumOfVertex());
System.out.println("边的个数 " + graph.getNumOfEdges());
System.out.println("A和B间的 weight= " + graph.getWeight("A", "B"));
}
public Graph(int n){
edges = new int[n][n];
}
// 插入节点
public void insertVertx(String vertex){
vertexList.add(vertex);
}
// 添加边
public void insertEdge(String vertexA, String vertexB, int weight){
int i = vertexList.indexOf(vertexA);
int j = vertexList.indexOf(vertexB);
if (edges[i][j] == 0) {
edges[i][j] = weight;
edges[j][i] = weight;
numOfEdges++;
}
}
public int getNumOfVertex(){
return vertexList.size();
}
public int getNumOfEdges(){
return numOfEdges;
}
// 得到权值
public int getWeight(String vertexA, String vertexB){
int i = vertexList.indexOf(vertexA);
int j = vertexList.indexOf(vertexB);
return edges[i][j];
}
public void printArr(){
for (int i = 0; i < edges.length; i++) {
for (int j = 0; j < edges.length; j++) {
System.out.print(edges[i][j] + " ");
}
System.out.println();
}
}
}
4. 图的遍历
深搜（DFS）：类似于树的先序遍历
w：列数
i：行数
可以这样理解：每次都在访问完当前节点后首先访问当前节点的第一个邻接节点
0 1 1 0 0
1 0 1 1 1
1 1 0 0 0
0 1 0 0 0
0 1 0 0 0
实现代码如下：
private boolean[] isVisited;
// 得到第一个邻接节点的下标
public int getFirstNeighbor(String vertex){
int cur = vertexList.indexOf(vertex); // 当前顶点下标
for (int j = 0; j < vertexList.size(); j++) {
if (edges[cur][j] > 0){ // 【自己和自己的 weight = 0】
return j;
}
}
return -1;
}
// 根据第一个节点的下标来获取下一个邻接节点【同一行，向右滑动的过程】
public int getNextNeighbor(int v1, int v2){ // v1：行数 v2：列数
for (int j = v2 + 1; j < vertexList.size() ; j++) {
if (edges[v1][j] > 0){
return j;
}
}
return -1;
}
// DFS 算法
// i：第一次就是 0
public void dfs(boolean[] isVisited, int i){
String s = vertexList.get(i);
System.out.print(s + " ");
isVisited[i] = true;
// 查找节点 i 的第一个邻接节点
int w = getFirstNeighbor(s);
while (w != -1){ // w 存在【如果 w 不存在的话，就会回溯到上一步了】
if (!isVisited[w]){ // 还没访问过
dfs(isVisited, w);
}
// 已经访问过
w = getNextNeighbor(i, w);
}
}
// 对 dfs进行重载，遍历我们所有的节点，并进行 dfs ===> 解决非连通图
public void dfs(){
// 遍历我们所有的顶点，进行DFS
for (int i = 0; i < getNumOfVertex(); i++) {
if (!isVisited[i]){
dfs(isVisited, i);
}
}
}
宽搜（BFS）：类似于数目的层次遍历
类似于分层搜索：
- 需要一个队列保存访问过的节点的顺序
- 以便于按照这个顺序来访问这些站点的邻接节点
经典习题：树的层次遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> list = new ArrayList<>();
List<List<Integer>> res = new ArrayList<>();
Deque<TreeNode> deque = new ArrayDeque<>();
public List<List<Integer>> levelOrder(TreeNode root) {
if (root == null){
return res;
}
deque.offer(root);
bfs();
return res;
}
public void bfs(){
while (!deque.isEmpty()){
int size = deque.size(); // 控制将上一轮的全部弹出去
while (size > 0){
TreeNode peek = deque.poll();
list.add(peek.val);
if (peek.left != null){
deque.offer(peek.left);
}
if (peek.right != null){
deque.offer(peek.right);
}
size--;
}
res.add(new ArrayList<>(list));
list.clear();
}
}
}
5. 最小生成树（MST：minimum spanning tree）：贪心策略不同
Prim【稠密图】---> 逐步加点
- 从已知某个顶点开始向外扩散，寻找最小的邻边，挨个将顶点加入集合【然后就以这个集合为一个整体了】
- 已加入集合的点不能再加入（否则会成环）
- 直到所有顶点加入集合，构成 MST
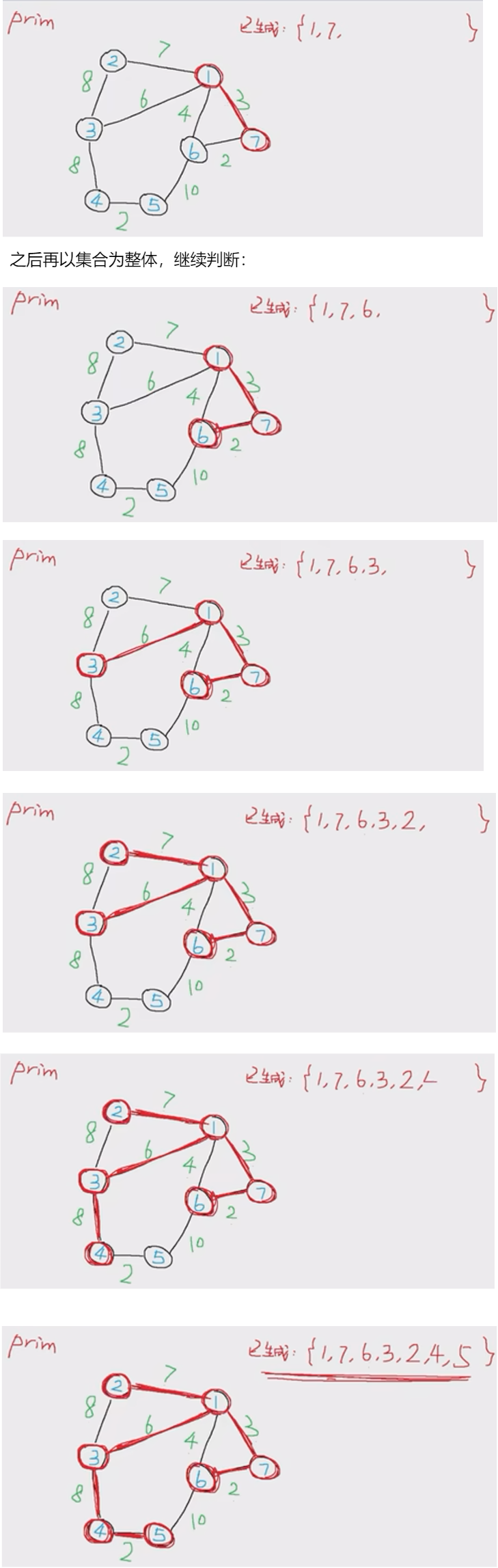
代码实现（三重循环）：
package com.alq.mst;
public class Prim {
static int weightTotal;
public static void main(String[] args) {
char[] data = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
int vertex = data.length;
int[][] weight = {{10000, 5, 7, 10000, 10000, 10000, 2},
{5, 10000, 10000, 9, 10000, 10000, 3},
{7, 10000, 10000, 10000, 8, 10000, 10000},
{10000, 9, 10000, 10000, 10000, 4, 10000},
{10000, 10000, 8, 10000, 10000, 5, 4},
{10000, 10000, 10000, 4, 5, 10000, 6},
{2, 3, 10000, 10000, 4, 6, 10000}
};
// 创建 MGraph 对象
MGraph mGraph = new MGraph(vertex);
// 创建一个 MiniTree
MiniTree miniTree = new MiniTree();
miniTree.createGraph(mGraph, vertex, data, weight);
miniTree.showGraph(mGraph);
miniTree.prim(mGraph, 0);
System.out.println("Prim 权值和为：" + weightTotal);
}
}
// 创建 MST
class MiniTree{
// 创建图的邻接矩阵
public void createGraph(MGraph mGraph, int vertex, char[] data, int[][] weight){
for (int i = 0; i < vertex; i++) {
mGraph.data[i] = data[i];
for (int j = 0; j < vertex; j++) {
mGraph.weight[i][j] = weight[i][j];
}
}
}
// 显示图的方法
public void showGraph(MGraph mGraph){
for (int i = 0; i < mGraph.vertex; i++) {
for (int j = 0; j < mGraph.vertex; j++) {
System.out.print(mGraph.weight[i][j] + "\t");
}
System.out.println();
}
}
// 编写 Prim 算法，得到 MST
/**
* @param mGraph：图
* @param v：从图的哪个顶点开始生成
*/
public void prim(MGraph mGraph, int v){
int[] visited = new int[mGraph.vertex];
// 将当前这个点标记为已访问
visited[v] = 1;
// 记录 2 个顶点的下标
int h1 = -1;
int h2 = -1;
// 将 miniWeigth 初始成一个大数，后面在遍历过程中，会被替换
int mimiWeight = 10000;
for (int k = 1; k < mGraph.vertex; k++) { // prim 算法结束后，有 n - 1 条边
for (int i = 0; i < mGraph.vertex; i++) { // 被访问过的节点
for (int j = 0; j < mGraph.vertex; j++) { // 还没有被访问的节点
if (visited[i] == 1 && visited[j] == 0 && mGraph.weight[i][j] < mimiWeight){
mimiWeight = mGraph.weight[i][j];
h1 = i;
h2 = j;
}
}
}
Prim.weightTotal += mimiWeight;
// 找到一条边是最小
System.out.println("边" + mGraph.data[h1] + "==>" + mGraph.data[h2] + " 权值:" + mimiWeight);
visited[h2] = 1; // 将找到的节点标记为：已经访问
// 重置：miniWeight 为最大值
mimiWeight = 10000;
}
}
}
class MGraph{
int vertex; // 表示图节点个数
char[] data; // 存放节点数据
int[][] weight; // 存放边（邻接矩阵）
public MGraph(int vertex) {
this.vertex = vertex;
data = new char[vertex];
weight = new int[vertex][vertex];
}
}
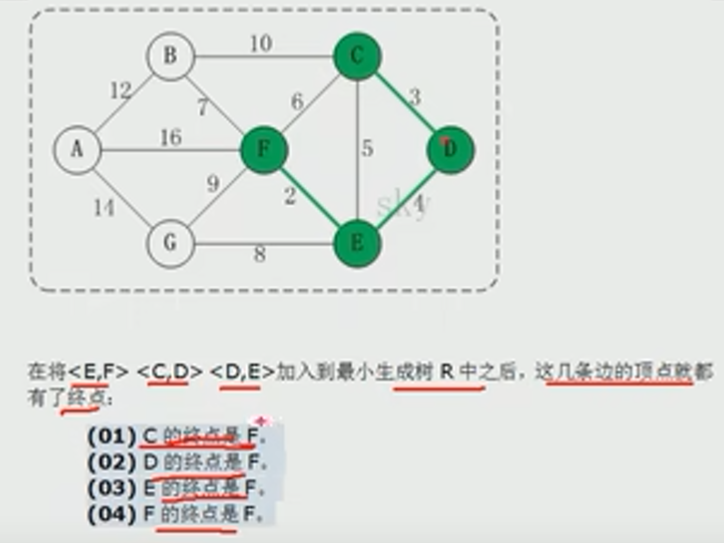
KRUSKAL【稀疏图】---> 对所有的边进行贪心，只需一次排序（使用并查集来辅助操作！！！）
- 从整个连通图最小的一条边开始贪心，边能最小就要最小的【只要不成环】
- 不断合并最后构成 MST
- 是否生成环，以及合并是利用 并查集 来辅助操作的
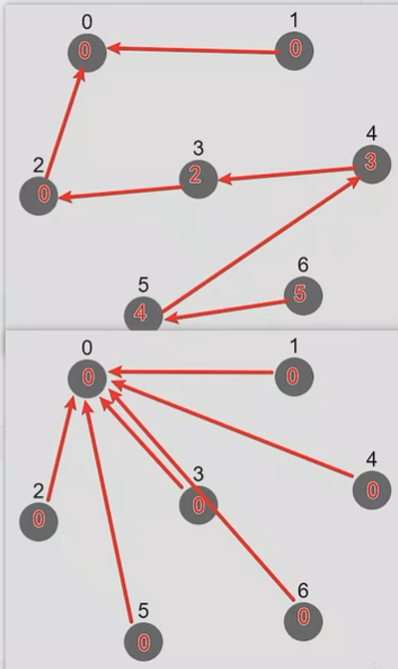
注意：初始化时，各自为一个集合，父节点就是自己本身（即：vertex[i] = i）
还有，不相交的2个集合，如果要合并的话
- 不能成环（2个父节点不能相同）
- 联合的话，是通过父节点来联合的
package com.llq.od;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
/**
* @Author: Ronnie LEE
* @Date: 2023/9/13 - 09 - 13 - 12:53
* @Description: com.llq.od
* @version: 1.0
*/
public class KRUSKAL {
static int[] vertex;
static int[][] matrix;
static List<EData> list = new ArrayList<>(); // 边的集合
static List<EData> result = new ArrayList<>();
private static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
vertex = new int[]{0, 1, 2, 3, 4, 5, 6};
matrix = new int[][]{
{0, 12, INF, INF, INF, 16, 14},
{12, 0, 10, INF, INF, 7, INF},
{INF, 10, 0, 3, 5, 6, INF},
{INF, INF, 3, 0, 4, INF, INF},
{INF, INF, 5, 4, 0, 2, 8},
{16, 7, 6, INF, 2, 0, 9},
{14, INF, INF, INF, 8, 9, 0}
};
init();
Collections.sort(list, (o1, o2) -> o1.weight - o2.weight); // 按照边的大小先排序【因为是最小生成树】
System.out.println(list);
for (int i = 0; i < list.size(); i++) {
EData eData = list.get(i);
int x = eData.start;
int y = eData.end;
if (union(x, y)){
result.add(list.get(i));
}
}
System.out.println(result);
}
public static void init(){
int len = vertex.length; // 长度
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++) { // 这里只统计上三角形即可
if (matrix[i][j] != INF){
list.add(new EData(i, j, matrix[i][j]));
}
}
}
}
// 查
public static int find(int x){
if (vertex[x] == x){
return x;
}
return find(vertex[x]);
}
// 并
public static boolean union(int x, int y){
// 2个不相交的集合联合，让其父亲联合即可
int father1 = find(x); // ⭐：一个初始父是自己！！！
int father2 = find(y);
if (father1 == father2){ // 2个不同的点最终都指向同一节点，说明已经同属一个集合了，无需添加！！！【否则会成环！】
return false;
}
vertex[father2] = father1; // 让 2个集合的大哥联合即可！！！
return true;
}
}
class EData{
int start; // 我们这里规定字符顺序小的为 父
int end;
int weight;
public EData(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public String toString() {
return "EData{" +
"start=" + start +
", end=" + end +
", weight=" + weight +
'}';
}
}
D:\Java\jdk-14.0.1\bin\java.exe "-javaagent:D:\IDEA2020.2.4\IntelliJ IDEA 2020.2.4\lib\idea_rt.jar=7424:D:\IDEA2020.2.4\IntelliJ IDEA 2020.2.4\bin" -Dfile.encoding=UTF-8 -classpath F:\JVM\out\production\JVM com.llq.od.KRUSKAL
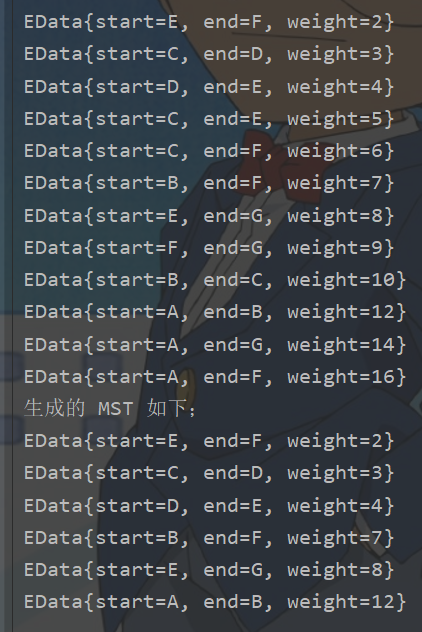
[EData{start=4, end=5, weight=2}, EData{start=2, end=3, weight=3}, EData{start=3, end=4, weight=4}, EData{start=2, end=4, weight=5}, EData{start=2, end=5, weight=6}, EData{start=1, end=5, weight=7}, EData{start=4, end=6, weight=8}, EData{start=5, end=6, weight=9}, EData{start=1, end=2, weight=10}, EData{start=0, end=1, weight=12}, EData{start=0, end=6, weight=14}, EData{start=0, end=5, weight=16}]
[EData{start=4, end=5, weight=2}, EData{start=2, end=3, weight=3}, EData{start=3, end=4, weight=4}, EData{start=1, end=5, weight=7}, EData{start=4, end=6, weight=8}, EData{start=0, end=1, weight=12}]
路径压缩【针对 find() 方法】
// 查
public static int find(int x){
if (vertex[x] == x){
return x;
}
return vertex[x] = find(vertex[x]);
}
