动态规划（DP）
DP
1. 理论
- 每个大问题的子问题都是最优的，所以才可以直接记录下来
- 在下次寻找子问题的最优解时，直接使用
与分治算法不同的是：
- 适合 dp 请求的问题，经分解得到的子问题往往不是互相独立的
- 即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步求解
2. 最优子结构
原问题的最优解包含子问题的最优解
3. 状态转移方程
- 写状态转移方程的程序，一般以递推的方式实现
- 虽然时间复杂度和记忆化搜索一样
- 而且在循环中会计算一些无意义的节点
- 但是递推免去了调用时进栈出栈的操作，而且避免了在递归时层数过多时栈溢出的情况
\(f(i,j)=max\left \{ f(i-1,j) ,f(i-1,j-w(i))+v(i)\right \}\)
4. 手办问题
| 手办名 | 价格 | 喜欢程度 |
|---|---|---|
| 兵长 | 10 | 24 |
| 蕾姆 | 4 | 9 |
| 小埋 | 4 | 9 |
| 和泉纱雾 | 5 | 10 |
| 空条承太郎 | 3 | 2 |
你现在 有 13 元
4.1 贪心算法
- 算出每个物品的性价比
- 优先买性价比高的物品
| 手办名 | 价格 | 喜欢程度 | 性价比 |
|---|---|---|---|
| 兵长 | 10 | 24 | 2.4 |
| 蕾姆 | 4 | 9 | 2.25 |
| 小埋 | 4 | 9 | 2.25 |
| 和泉纱雾 | 5 | 10 | 2 |
| 空条承太郎 | 3 | 2 | 0.67 |
最终的喜欢程度为：24 + 2 = 26
4.2 0-1 背包问题
| 背包问题 | 说明 |
|---|---|
| 0-1 背包 | 每个物品最多一个 |
| 完全背包 ==> 可以转化成 0-1 背包 | 每种物品无限件 |
| 手办是一个整体 |
- 你不能只买🐻和大腿，按照比例给钱，所以不能用贪心来解决
普通递归实现
# f(i, j)：当还剩 j 元钱时，前 i 个物品能达到的最大喜欢值
# max【不买这个商品的价值，买这个商品的价值】
\(f(i,j)=max\left \{ f(i-1,j) ,f(i-1,j-w(i))+v(i)\right \}\)
public class jianchi {
static int[] price = new int[]{10, 4, 4, 5, 3};
static int[] value = new int[]{24, 9, 9, 10, 2};
public static void main(String[] args) {
System.out.println(f(5, 13));
}
public static int f(int i, int j){ // 当还剩 j 元钱时，前 i 个物品能达到的最大喜欢值
// baseCase
if (i == 0){ // 当没有物品，价值为 0
return 0;
}
if (j < price[i - 1]){ // 买不起当前物品，就无需比较
return f(i - 1, j);
}
// 不买第 n 个物品
// 买第 n 个物品，总钱数就会减少，接下来就用 j - price[i - 1]钱考虑剩下的 i - 1个物品喽
return Math.max(f(i - 1, j), f(i - 1, j - price[i - 1]) + value[i - 1]); // 下标从 0 开始
}
}
递推（记忆化数组）
那么，这个 0/1 背包问题是否满足 最优子结构 呢???
能不能用 记忆化搜索 来优化这一算法???
| 已知条件 | |
|---|---|
| \(n\) 个物品 | \(T\) 元钱 |
| \(W_{i}\) 价格 | \(V_{i}\) 喜欢值 |
| \(X_{i}\epsilon \left \{ 0,1 \right \}\) | 是否买 |
这样问题可以转化为：
\[max\sum_{i=1}^{n}V_{i}X_{i}\left ( \sum_{i=1}^{n}W_{i}X_{i}\leqslant T \right )
\]
证明：上述公式是具有 最优子结构 的。
- 设 \(\left ( y_{1},y_{2}……y_{n} \right )\) 是 \(max\sum_{i=1}^{n}V_{i}X_{i}\) 最优解
- 那么 \(\left ( y_{2},y_{3}……y_{n} \right )\) 是子问题 \(max\sum_{i=2}^{n}V_{i}X_{i}\left ( \sum_{i=2}^{n}W_{i}X_{i}\leqslant T- W_{1}X_{1}\right )\)
- 使用 反证法
- 假设子问题存在 \(\left ( Z_{2},Z_{3}……Z_{n} \right )\) 是最优解，那么 \(\left ( y_{2},y_{3}……y_{n} \right )\) 就不是它的最优解
- 则：\(\sum_{i=2}^{n}V_{i}y_{i}\leqslant \sum_{i=2}^{n}V_{i}Z_{i}\)
- 两边同时加上 \(V_{1}y_{1}\)
- \(\sum_{i=2}^{n}V_{i}y_{i}+V_{1}y_{1}\leqslant \sum_{i=2}^{n}V_{i}Z_{i}+V_{1}y_{1}\) ===> 得出 \(\left ( y_{1},y_{2}……y_{n} \right )\) 并不是大问题的最优解，最优解是 \(\left ( y_{1},Z_{2}……Z_{n} \right )\)
- 就与我们最开始的设定相矛盾了
- 证明这个问题是有最优子结构的
使用记忆化搜索优化递推：
public class jianchi {
static int[] price = new int[]{10, 4, 4, 5, 3};
static int[] value = new int[]{24, 9, 9, 10, 2};
// 记忆数组 dp，第一个角标表示物品，第二个角标表示我们有多少钱
// 防止数组越界，在开数据空间时，增加一个空间
static int[][] dp = new int[6][14];
public static void main(String[] args) {
System.out.println(f(5, 13));
}
public static int f(int i, int j){ // 当还剩 j 元钱时，前 i 个物品能达到的最大喜欢值
// baseCase
if (i == 0){ // 当没有物品，价值为 0
return 0;
}
if (dp[i][j] != 0){
return dp[i][j];
}
if (j < price[i - 1]){ // 买不起当前物品，就无需比较
return dp[i][j] = f(i - 1, j);
}
// 不买第 n 个物品
// 买第 n 个物品，总钱数就会减少，接下来就用 j - price[i - 1]钱考虑剩下的 i - 1个物品喽
return dp[i][j] = Math.max(f(i - 1, j), f(i - 1, j - price[i - 1]) + value[i - 1]);
}
}
记忆化搜索，时间复杂度：\(O(n*t)\)
- n：物品个数
- t：拥有的钱
下面用递推实现：
从已知 ---> 未知
- 即：物品数从1个开始计算
- 同时利用了数组未赋值时，初始值是0【我有 13 块钱，但是数组下标是从 0 开始的哦，所以大小要开成 14】
package com.alq.dp;
public class Bag {
static int[] price = new int[]{10, 4, 4, 5, 3};
static int[] value = new int[]{24, 9, 9, 10, 2};
// 记忆数组 dp，第一个角标表示物品，第二个角标表示我们有多少钱
// 防止数组越界，在开数据空间时，增加一个空间
static int[][] dp = new int[6][14];
public static void main(String[] args) {
System.out.println(f(5, 13));
}
public static int f(int i, int j){ // 当还剩 j 元钱时，前 i 个物品能达到的最大喜欢值
// 递推实现
// 遍历记忆数组
for (int k = 1; k <= i ; k++) { // 物品个数
for (int l = j; l >= 0 ; l--) { // 拥有的钱
if ( l < price[k - 1]){
dp[k][l] = dp[k - 1][l]; // 买不起当前物品 【数组，未赋值时，默认值是 0】
}else {
// 状态转移方程
dp[k][l] = Math.max(dp[k - 1][l], dp[k - 1][l - price[k - 1]] + value[k - 1]);
}
}
}
return dp[i][j];
}
}
我们发现：当状态转移时
- 当前状态只与上个状态有关
- 只在 i - 1 或 i + 1 这一行中取需要的值
- 再前面状态的值便没有用了
定义一个数组，存放放入物品信息
| 手办名 | 价格 | 喜欢程度 |
|---|---|---|
| 兵长 | 10 | 24 |
| 蕾姆 | 4 | 9 |
| 小埋 | 4 | 9 |
| 和泉纱雾 | 5 | 10 |
| 空条承太郎 | 3 | 2 |
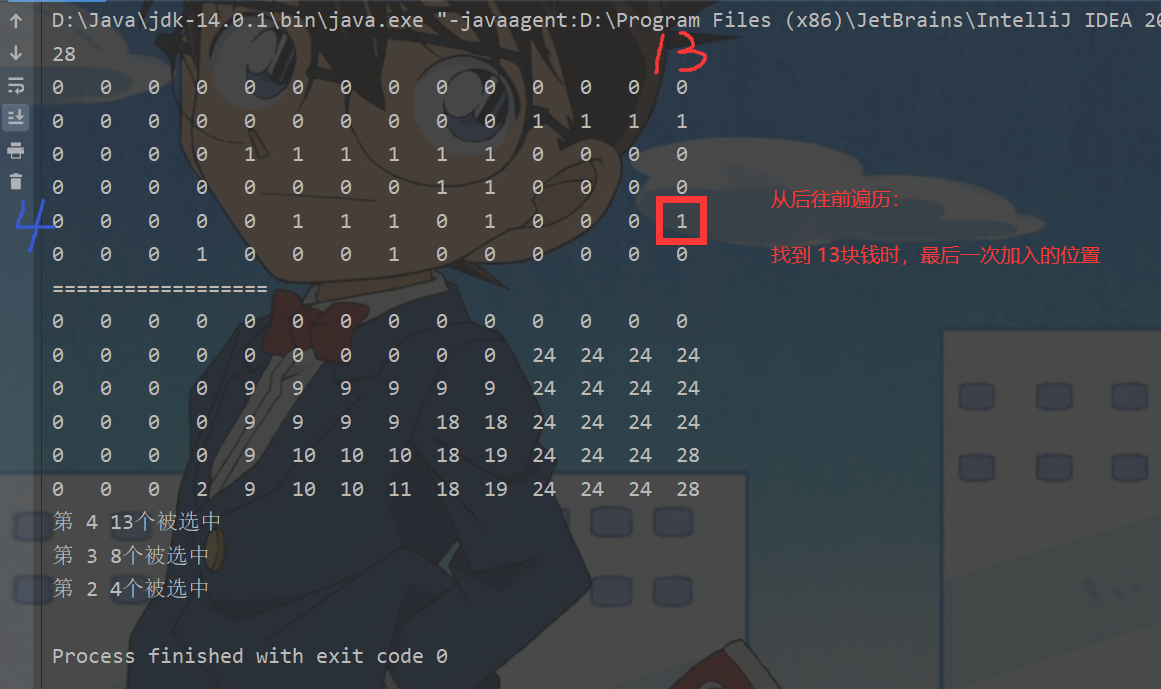
然后逐步向上查询：
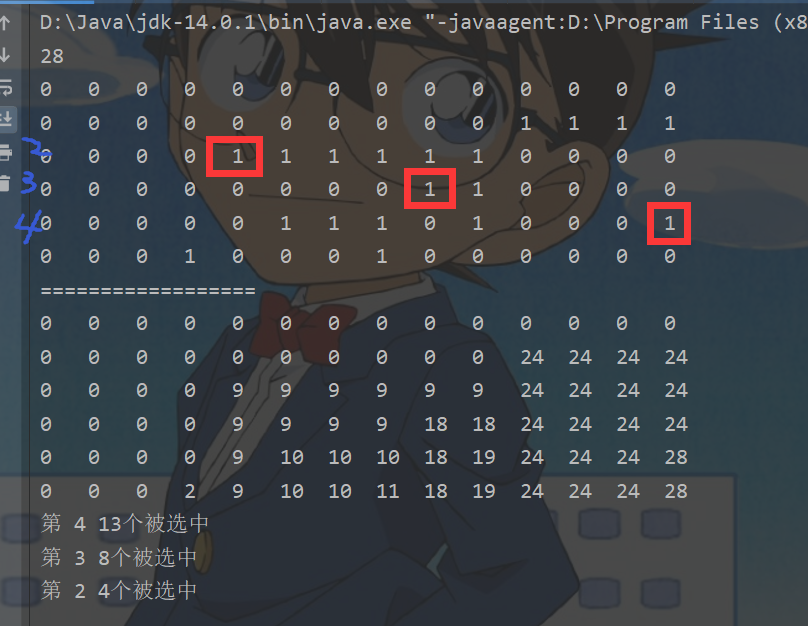
int i = path.length - 1;
int j = path[0].length - 1;
while (i > 0 && j > 0){
if (path[i][j] == 1){
System.out.println("第 " + i + " " + j + "个被选中");
j -= price[i - 1];
}
i--;
}
package com.alq.dp;
public class Bag {
static int[] price = new int[]{10, 4, 4, 5, 3};
static int[] value = new int[]{24, 9, 9, 10, 2};
// 记忆数组 dp，第一个角标表示物品，第二个角标表示我们有多少钱
// 防止数组越界，在开数据空间时，增加一个空间
static int[][] dp = new int[6][14];
static int[][] path = new int[6][14];
public static void main(String[] args) {
System.out.println(f(5, 13));
for (int[] ints : path) {
for (int anInt : ints) {
System.out.print(anInt + "\t");
}
System.out.println();
}
System.out.println("==================");
for (int[] ints : dp) {
for (int anInt : ints) {
System.out.print(anInt+"\t");
}
System.out.println();
}
// 输出我们最后放入的是那些物品
int i = path.length - 1;
int j = path[0].length - 1;
while (i > 0 && j > 0){
if (path[i][j] == 1){
System.out.println("第 " + i + " " + j + "个被选中");
j -= price[i - 1];
}
i--;
}
}
public static int f(int i, int j){ // 当还剩 j 元钱时，前 i 个物品能达到的最大喜欢值
// 递推实现
// 遍历记忆数组
for (int k = 1; k <= i ; k++) { // 物品个数
for (int l = j; l >= 0 ; l--) { // 拥有的钱
if ( l < price[k - 1]){
dp[k][l] = dp[k - 1][l]; // 买不起当前物品 【数组，未赋值时，默认值是 0】
}else {
// 状态转移方程
// dp[k][l] = Math.max(dp[k - 1][l], dp[k - 1][l - price[k - 1]] + value[k - 1]);
if (dp[k - 1][l] < dp[k - 1][l - price[k - 1]] + value[k - 1]){ // 买
dp[k][l] = dp[k - 1][l - price[k - 1]] + value[k - 1];
// 将当前情况记录到 path
path[k][l] = 1;
}else {
dp[k][l] = dp[k - 1][l];
}
}
}
}
return dp[i][j];
}
}
滚动数组
于是空间复杂度可以优化为：
\(O(n*t)=O(t)\)
