洛谷 P5057 [CQOI2006]简单题 题解
P5057 [CQOI2006]简单题
题目描述
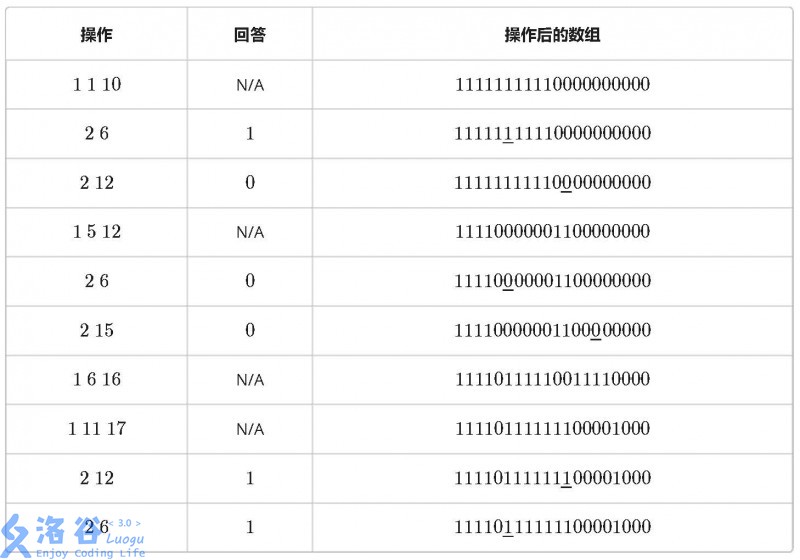
有一个 n 个元素的数组,每个元素初始均为 0。有 m 条指令,要么让其中一段连续序列数字反转——0 变 1,1 变 0(操作 1),要么询问某个元素的值(操作 2)。 例如当 n = 20 时,10 条指令如下:
输入格式
第一行包含两个整数 n, m,表示数组的长度和指令的条数; 以下 m 行,每行的第一个数 t 表示操作的种类:
若 t = 1,则接下来有两个数 L, R,表示区间 [L, R] 的每个数均反转; 若 t = 2,则接下来只有一个数 i,表示询问的下标。
输出格式
每个操作 2 输出一行(非 0 即 1),表示每次操作 2 的回答。
输入输出样例
输入 #1
20 10
1 1 10
2 6
2 12
1 5 12
2 6
2 15
1 6 16
1 11 17
2 12
2 6
输出 #1
1
0
0
0
1
1
说明/提示
对于 50% 的数据,\(1 ≤ n ≤ 10^3\),$ 1 ≤ m ≤ 10^4$; 对于 100% 的数据,\(1 ≤ n ≤ 10^5\), \(1 ≤ m ≤ 5 × 10^5\),保证 L ≤ R。
【树状数组】
【思路】
树状数组
【题目大意】
区间反转和单点询问
【题目分析】
区间反转我首先想到了是线段树
用lazy标记某个区间反转过几次
但是我是抱着练习树状数组的目的
来做的这道题
所以必须用树状数组做!!!
不过树状数组该怎么办呢?
难不成枚举每一个点然后修改?
不对
这个时候情不自禁想到了那个优美的东西
差分
类似树状数组模板2的方法
差分一下下就可以很轻松标记翻转次数了
【核心思路】
树状数组维护差分数组
差分数组修改区间
只需要在区间左端点加上修改的值
在右端点之后减去修改的值就好了
求某个位置上的值
就是这个位置之前(包括这个位置)的和
也符合树状数组里面的sum
就不需要做差了
最后按照%2来输出就好了
因为翻转两次之后会回到原来的情况
【思路】
#include<iostream>
#include<cstdio>
#define int long long
using namespace std;
const int Max = 100006;
int a[Max];
int n,m;
int read()
{
int sum = 0,fg = 1;
char c = getchar();
while(c < '0' || c > '9')
{
if(c == '-')fg = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
{
sum = sum * 10 + c - '0';
c = getchar();
}
return sum * fg;
}
int lowbit(int x)
{
return x & -x;
}
void add(int x,int y)
{
while(x <= n)
{
a[x] += y;
x += lowbit(x);
}
}
int sum(int x)
{
int ans = 0;
while(x > 0)
{
ans += a[x];
x -= lowbit(x);
}
return ans;
}
signed main()
{
n = read(),m = read();
for(register int i = 1;i <= m;++ i)
{
int t = read();
if(t == 1)
{
int l = read(),r = read();
add(l,1);
add(r + 1,-1);
}
else
{
int qwq = read();
cout << sum(qwq) % 2 << endl;
}
}
return 0;
}
【线段树】
【思路】
线段树
首先感谢@大魔鬼灿灿 巨佬帮我滑鼠标
用树状数组做过了,但是还是可以用线段树做的
所以也拿线段树来做回顾一下线段树,
然后没想到调试了两个小时
【核心思路】
sum记录这个点被修改的次数
因为是区间修改和单点查询
所以线段树中只要不是叶子节点的sum就不需要求了
只用来lazy标记就可以了
然后该下放到叶子节点的时候就下发好了
最后输出记录的修改次数%2
【注意事项】
不管不是叶子节点的sum没问题
但是有的修改的时候却是单点修改
所以该sum++还是得sum++的
把全部节点的sum都当叶子节点的来处理
加上修改的次数
也就是lazy值就好了
【完整代码】
#include<iostream>
#include<cstdio>
#define lson (k << 1)
#define rson (k << 1 | 1)
using namespace std;
int read()
{
int sum = 0,fg = 1;
char c = getchar();
while(c < '0' || c > '9'){if(c == '-')fg = -1;c = getchar();}
while(c >= '0' && c <= '9'){sum = sum * 10 + c - '0';c = getchar();}
return sum * fg;
}
const int Max = 100004;
struct node
{
int l,r;
int lazy;
int sum;
}a[Max << 2];
int n,m;
int opx,opl,opr;
void build(int k,int l,int r)
{
a[k].l = l;a[k].r = r;
if(l == r)
return;
int mid = (l + r) >> 1;
build(lson,l,mid);
build(rson,mid + 1,r);
return;
}
void down(int k)
{
if(a[k].lazy)
{
a[lson].sum += a[k].lazy;
a[rson].sum += a[k].lazy;
a[lson].lazy += a[k].lazy;
a[rson].lazy += a[k].lazy;
a[k].lazy = 0;
}
}
void change(int k)
{
if(opl <= a[k].l && opr >= a[k].r)
{
a[k].lazy ++;
a[k].sum++;
return;
}
down(k);
int mid = (a[k].l + a[k].r) >> 1;
if(opl <= mid)change(lson);
if(opr > mid)change(rson);
a[k].sum = a[lson].sum + a[rson].sum;
}
void query(int k)
{
if(a[k].l == opx && a[k].r == opx)
{
cout << a[k].sum % 2 << endl;
return;
}
down(k);
int mid = (a[k].l + a[k].r) >> 1;
if(opx <= mid) query(lson);
if(opx > mid) query(rson);
}
int main()
{
n = read(),m = read();
build(1,1,n);
for(register int i = 1;i <= m;++ i)
{
int qwq = read();
if(qwq == 1)
{
opl = read(),opr = read();
change(1);
}
else
{
opx = read();query(1);
}
}
return 0;
}

