浅谈二维前缀和
【二维前缀和】
【一维前缀和】
一维前缀和顾名思义
就是一维的前缀和
前缀和是什么呢？
前缀和就是到目前为止全部的和是多少
一维就是单纯的一串数
他的前缀和就成了一维前缀和
【举例】
\(1\ 2 \ 3 \ 4 \ 5 \ 6\)
他的前缀和依次就是 \(1 \ 3 \ 6 \ 10 \ 15 \ 21\)
\(i\)位置上的前缀和就是从第一个数到第\(i\)个数全部数的和
这样就很显然的知道了什么是一维前缀和了吧？
【二维前缀和是什么】
二维前缀和顾名思义
就是二维的前缀和
二维很显然了
有x轴和y轴也就是一个面
这很显然
那二维前缀和中一个f[i][j]表示的意思就是
以（1,1）为左上角以（i,j）为右下角这个矩阵里面数的和
如图
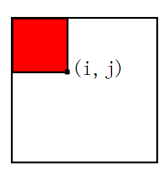
f[i][j]表示的就是图中红色的部分
【二维前缀和怎么求】
这里先不说，先假设自己知道了每\(f[i][j]\)二维前缀和是多少
（这个锅我背，因为一开始设计的问题，导致先解释的求矩阵值而没有解释求\(f[i][j]\)的值，因这两个很相似所以说一个就过了，先说了求矩阵那这里再说求点就有点重复了我嫌麻烦，所二维前缀和点的值就在最后说一下吧，在已知求矩阵的情况下）
【二维前缀和求矩阵元素和】
二维前缀和可以用来干什么呢？
一维前缀和你可以用来O(1)求某个点的值
那么类比一下
二维前缀和也是可以用来求某个矩阵的值的
但是怎么来求呢？
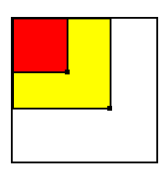
就如图中
知道了两个点的位置和他们的二维前缀和
图中红色是左上角的那个点的二维前缀和
红色+黄色部分是右下角的那个点的二维前缀和
是不是可以用这个来求出他们之间的矩阵的和呢？
也就是这一部分：
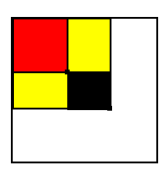
图中黑色的部分就是我们要求的那个矩阵和
看到这里yy一下
是不是可以通过某些奇怪的方法求出黑色部分是多少？
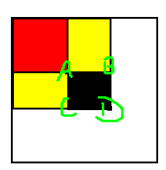
D点表示的二维前缀和值是红色部分+两个黄色部分+黑色部分
A点表示的是红色部分
B点表示的是上面的黄色部分+红色部分
C点表示的是下面的黄色部分+红色部分
这样是不是发现有什么神奇的东西快要出现了
这里面只有D的前缀和里面包括黑色部分
只要减去D里面的哪两个黄色部分和红色部分是不是就剩下了我们要求的黑色部分了？
那怎么减去呢？
可以这样：
D - B - C + A
这就是二维前缀和最重要的部分了
化成二维数组的形式就是这样的
【为什么上文成立】
继续看上面那张图
由D-B-C+A到方程式这个很显然所以就不多说了
只要证明出D-B-C+A是正确的那就没有问题了
这个可以化成：
红色部分+上面的黄色部分+下面的黄色部分+黑色部分-上面的黄色部分-红色部分-下面的黄色部分-红色部分+红色部分
这样是不是很巧妙的就只剩下了黑色部分
所以成立
【补充 —— 二维前缀和怎么求】
这个可以类比上面求矩阵的思想
只是这个矩阵的右下角是（i，j），左上角也是（i,j）
就是一个11的矩阵
所以也是很好求的
但是上面是已知D，A，B，C求黑色部分
这里你只知道A，B，C和黑色部分
因为是一个11的矩阵吗
所以黑色部分就只有一个元素也就是（i，j）坐标上的那个元素值
所以就可以个加法变减法，减法变加法一个性质的
通过A，B，C和黑色部分来求出D
D点表示的二维前缀和值是红色部分+两个黄色部分+黑色部分
A点表示的是红色部分
B点表示的是上面的黄色部分+红色部分
C点表示的是下面的黄色部分+红色部分
所以D就可以等于B+C-D+黑色部分：
上面的黄色部分+红色部分+下面的黄色部分+红色部分-红色部分+黑色部分
=上面的黄色部分+红色部分+下面的黄色部分+黑色部分
刚好等于D
方程式为
【模板】
给个小板子
查询某个矩阵里面数的总和
#include<iostream>
#include<cstdio>
#define int long long
using namespace std;
const int Max = 1003;
int a[Max][Max];
int f[Max][Max];
signed main()
{
freopen("acioi.in","r",stdin);
int n,m,c;
cin >> n >> m >> c;
for(register int i = 1;i <= n;++ i)
for(register int j = 1;j <= m;++ j)
cin >> a[i][j],f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];
int k;
cin >> k;
for(register int i = 1;i <= k;++ i)
{
int x1,x2,y1,y2;//x1,y1是左上角的坐标，另一对是右下角的坐标
cin >> x1 >> y1 >> x2 >> y2;
cout << f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1];
}
cout << M << endl;
return 0;
}
【注意】
上面有许多坐标减去1的情况
是因为左上角的那个点表示的前缀和包括左上角的值
但是左上角这个点也包括在我们要求的矩阵内
所以不应该减去
这就是-1的原因了
其他不一样的类比一下就好了哈
