牛客国庆集训派对Day_1~3
Day_1
A.Tobaku Mokushiroku Kaiji
题目描述
Kaiji正在与另外一人玩石头剪刀布。双方各有一些代表石头、剪刀、布的卡牌,每局两人各出一张卡牌,根据卡牌的内容决定这一局的胜负。胜负规则为:石头赢剪刀、剪刀赢布、布赢石头、相同为平局。每张卡牌至多被使用一次。
已知双方的卡牌数量,问Kaiji最多赢几局?
输入描述:
一行六个数字0 ≤ a, b, c, d, e, f ≤ 50,a,b,c分别表示Kaiji的石头、剪刀、布的牌的数量,d,e,f分别表示此时另一人的石头、剪刀、布的牌的数量。
输出描述:
一个整数表示Kaiji最多赢几局。
示例1
输入
29 7 41 14 12 42
输出
33
解题思路:简单取三个最小即可。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 int a,b,c,d,e,f,ans; 5 int main(){ 6 while(cin>>a>>b>>c>>d>>e>>f){ 7 ans=a>e?e:a; 8 ans+=b>f?f:b; 9 ans+=c>d?d:c; 10 cout<<ans<<endl; 11 } 12 return 0; 13 }
C.Utawarerumono
题目描述
算术是为数不多的会让Kuon感到棘手的事情。通常她会找Haku帮忙,但是Haku已经被她派去买东西了。于是她向你寻求帮助。
给出一个关于变量x,y的不定方程ax+by=c,显然这个方程可能有多个整数解。Kuon想知道如果有解,使得p2*x2+p1*x+q2*y2+q1*y最小的一组整数解是什么。为了方便,你只需要输出p2*x2+p1*x+q2*y2+q1*y的最小值。
给出一个关于变量x,y的不定方程ax+by=c,显然这个方程可能有多个整数解。Kuon想知道如果有解,使得p2*x2+p1*x+q2*y2+q1*y最小的一组整数解是什么。为了方便,你只需要输出p2*x2+p1*x+q2*y2+q1*y的最小值。
输入描述:
第一行三个空格隔开的整数a,b,c(0 ≤ a,b,c≤ 10^5)。
第二行两个空格隔开的整数p1,p2,(1 ≤ p1,p2 ≤ 10^5)。
第三行两个空格隔开的整数q1,q2,(1 ≤ q1,q2 ≤ 10^5)。
输出描述:
如果方程无整数解,输出“Kuon”。
如果有整数解,输出p2*x^2+p1*x+q2*y^2+q1*y的最小值。
示例2
输入
1 2 3 1 1 1 1
输出
4
解题思路:法一: ∵0 ≤ a,b,c ≤ 1e5, ∴ x∈[-1e5,2e5] ∧ x∈Ν。因此只需暴力枚举一下x的值,注意模数不能作0,单独分情况讨论即可。法二:扩展gcd+公式推导。
AC代码一:暴力。
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 LL a,b,c,p1,p2,q1,q2,x,y,ans; 5 int main(){ 6 while(cin>>a>>b>>c){ 7 cin>>p1>>p2>>q1>>q2;ans=LONG_LONG_MAX; 8 if((a&&!(c%a))&&!b)x=c/a,ans=p2*x*x+p1*x; 9 else if(!a&&(b&&!(c%b)))y=c/b,ans=q2*y*y+q1*y; 10 else if(a&&b){ 11 for(LL i=-100000;i<=200000;++i){ 12 y=(c-a*i); 13 if(y%b==0)y/=b,ans=min(ans,p2*i*i+p1*i+q2*y*y+q1*y); 14 } 15 } 16 if(ans!=LONG_LONG_MAX)cout<<ans<<endl; 17 else cout<<"Kuon"<<endl; 18 } 19 return 0; 20 }
AC代码二:扩展欧几里得+公式推导。
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 typedef long double LD; 5 LL a,b,c,p1,p2,q1,q2,x,y,ans,gcd,ubt;LD A,B,C,t; 6 LL f(LL x,LL y){return p2*x*x+p1*x+q2*y*y+q1*y;} 7 LL exGcd(LL a,LL b,LL &x,LL &y){ 8 if(b==0){x=1;y=0;return a;} 9 LL r=exGcd(b,a%b,x,y); 10 LL t=x;x=y;y=t-a/b*y; 11 return r; 12 } 13 int main(){ 14 while(cin>>a>>b>>c){ 15 cin>>p1>>p2>>q1>>q2;ans=LONG_LONG_MAX; 16 gcd=exGcd(a,b,x,y); 17 if((c%gcd)||!gcd){cout<<"Kuon"<<endl;continue;} 18 if((a&&!(c%a))&&!b)ans=f(c/a,0); 19 else if(!a&&(b&&!(c%b)))ans=f(0,c/b); 20 else{ 21 a/=gcd,b/=gcd,c/=gcd,x*=c;//x为exgcd求出来的一个解即x0 22 A=p2+1.0*a*a*q2/(b*b); 23 B=p1-2.0*a*c*q2/(b*b)-1.0*a*q1/b; 24 C=1.0*q2*c*c/(b*b)+1.0*q1*c/b; 25 t=-B/(2.0*A);//化简后得到的函数的对称轴 26 ubt=(t-x)/b;//通解:x=x0+b*k ----> t=x0+b*ubt ----> 倍数ubt=(t-x0)/b 27 for(LL i=ubt-3;i<=ubt+3;++i){//枚举倍数ubt的上下几个值即可 28 LL x1=x+b*i;//通解:x=x0+b*i 29 LL y1=(c-a*x1)/b; 30 ans=min(ans,f(x1,y1)); 31 } 32 cout<<ans<<endl; 33 } 34 } 35 return 0; 36 }
E.Eustia of the Tarnished Wings
题目描述
Novus Aither是一个潜藏着多个势力的城市。每个势力都有一个唯一的领导人,每个领导人有一个属性值。如果两个势力的领导人的属性值分别为a,b,且|a-b| ≤ m,说明这两个领导人的思想有一定的相似之处,这两个势力可以合并,新的领导人可以指定为原来的两个领导人中的任意一个。新产生的势力可以依照相同的规则,继续与其他势力合并。问在所有可能的情况中,最少会剩下几个势力。
输入描述:
第一行两个空格隔开的整数n(1 ≤ n ≤ 10^6),m(0 ≤ m ≤ 10^9)。n代表当前势力的个数。m的含义如题目描述。
第二行n个空格隔开的整数di(0 ≤ di ≤ 10^9),代表第i个势力的领导人的属性值。
输出描述:
输出一个数表示势力的最少数量。
示例1
输入
4 1 2 1 3 10
输出
2
解题思路:简单贪心,排个序,每次取最大的一个-->后者,符合前后两个属性值之差不大于m的个数为cnt,那么剩下势力的最少数量为n-cnt。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const int maxn=1e6+5; 5 int n,m,cnt,a[maxn]; 6 int main(){ 7 while(cin>>n>>m){ 8 for(int i=0;i<n;++i)cin>>a[i]; 9 sort(a,a+n);cnt=0; 10 for(int i=1;i<n;++i) 11 if(a[i]-a[i-1]<=m)cnt++; 12 cout<<n-cnt<<endl; 13 } 14 return 0; 15 }
L.New Game!
题目描述
Eagle Jump公司正在开发一款新的游戏。Hifumi Takimoto作为其中的员工,获得了提前试玩的机会。现在她正在试图通过一个迷宫。
这个迷宫有一些特点。为了方便描述,我们对这个迷宫建立平面直角坐标系。迷宫中有两条平行直线 L1:Ax+By+C1=0, L2:Ax+By+C2=0,还有 n 个圆$ C_i : (x - x_i)^2 + (y - y_i)^2 = r_i^2 $ 。角色在直线上、圆上、园内行走不消耗体力。在其他位置上由S点走到T点消耗的体力为S和T的欧几里得距离。
Hifumi Takimoto想从 L1 出发,走到 L2 。请计算最少需要多少体力。
这个迷宫有一些特点。为了方便描述,我们对这个迷宫建立平面直角坐标系。迷宫中有两条平行直线 L1:Ax+By+C1=0, L2:Ax+By+C2=0,还有 n 个圆$ C_i : (x - x_i)^2 + (y - y_i)^2 = r_i^2 $ 。角色在直线上、圆上、园内行走不消耗体力。在其他位置上由S点走到T点消耗的体力为S和T的欧几里得距离。
Hifumi Takimoto想从 L1 出发,走到 L2 。请计算最少需要多少体力。
输入描述:
第一行五个正整数 n,A,B,C1,C2(1≤ n ≤ 1000, -10000 ≤ A,B,C1,C2 ≤ 10000),其中 A,B 不同时为 0。
接下来 n 行每行三个整数 x,y,r(-10000 ≤ x,y ≤ 10000, 1≤ r ≤ 10000) 表示一个圆心为 (x,y),半径为 r 的圆。
输出描述:
仅一行一个实数表示答案。与正确结果的绝对误差或者相对误差不超过 10^(-4) 即算正确。
示例1
输入
2 0 1 0 -4 0 1 1 1 3 1
输出
0.236068
解题思路:求直线L1到直线L2间需要越过的空白距离的最小值,dp一下即可。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1005; 4 struct cyc{double x,y,r,dis1,dis2;}arr[maxn]; 5 bool cmp(cyc a,cyc b){return a.dis1<b.dis1;} 6 int n;double A,B,C1,C2,ans,dp[maxn]; 7 int main(){ 8 while(cin>>n>>A>>B>>C1>>C2){ 9 for(int i=0;i<n;++i){ 10 cin>>arr[i].x>>arr[i].y>>arr[i].r; 11 arr[i].dis1=fabs(A*arr[i].x+B*arr[i].y+C1)/sqrt(A*A+B*B);//求出每个圆心到直线L1的距离 12 arr[i].dis2=fabs(A*arr[i].x+B*arr[i].y+C2)/sqrt(A*A+B*B);//求出每个圆心到直线L2的距离 13 } 14 sort(arr,arr+n,cmp);ans=fabs(C1-C2)/sqrt(A*A+B*B);//最少需要消耗的体力为两直线间的距离 15 for(int i=0;i<n;++i){ 16 dp[i]=max(arr[i].dis1-arr[i].r,0.0);//先初始化到直线L1的空白距离-->非负数 17 for(int j=0;j<i;++j)//再处理两直线的中间所有圆之间的空白最短的距离 18 dp[i]=min(dp[i],dp[j]+max(0.0,sqrt((arr[i].x-arr[j].x)*(arr[i].x-arr[j].x)+(arr[i].y-arr[j].y)*(arr[i].y-arr[j].y))-(arr[i].r+arr[j].r))); 19 ans=min(ans,dp[i]+max(0.0,arr[i].dis2-arr[i].r));//最后处理当前的一个圆到直线L2的空白距离-->非负数 20 } 21 cout<<setiosflags(ios::fixed)<<setprecision(6)<<ans<<endl; 22 } 23 return 0; 24 }
Day_2
A.矩阵乘法
题目描述
深度学习算法很大程度上基于矩阵运算。例如神经网络中的全连接,本质上是一个矩阵乘法;而卷积运算也通常是用矩阵乘法来完成的。有一些科研工作者为了让神经网络的计算更快捷,提出了二值化网络的方法,就是将网络权重压缩成只用两种值表示的形式,这样就可以用一些 trick 加速计算了。例如两个二进制向量点乘,可以用计算机中的与运算代替,然后统计结果中 1 的个数即可。
然而有时候为了降低压缩带来的误差,只允许其中一个矩阵被压缩成二进制。这样的情况下矩阵乘法运算还能否做进一步优化呢?给定两个整数矩阵A, B,计算矩阵乘法 C = A x B。为了减少输出,你只需要计算 C 中所有元素的的异或和即可。
输入描述:
第一行有三个整数 N, P, M, 表示矩阵 A, B 的大小分别是 N x P, P x M 。
接下来 N 行是矩阵 A 的值,每一行有 P 个数字。第 i+1 行第 j 列的数字为 A_i,j, A_i,j
用大写的16进制表示(即只包含 0~9, A~F),每个数字后面都有一个空格。
接下来 M 行是矩阵 B 的值,每一行是一个长为 P 的 01字符串。第 i + N + 1 行第 j 个字符表示 B_j,i的值。
输出描述:
一个整数,矩阵 C 中所有元素的异或和。
示例1
输入
4 2 3 3 4 8 A F 5 6 7 01 11 10
输出
2
说明
矩阵 C 的值为:
4 7 3
10 18 8
5 20 15
7 13 6
备注:
2 ≤ N, M ≤ 4096, 1 ≤ P ≤ 64, 0 ≤ A_i,j < 65536.
解题思路:01矩阵,预处理一下即可。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,p,m,btr,ans,tmp,a[4096][72],b[72][4096],c[4096][8][256],d[8][4096];char str[70]; 4 int main(){ 5 while(~scanf("%d%d%d",&n,&p,&m)){ 6 for(int i=0;i<n;++i) 7 for(int j=0;j<p;++j) 8 scanf("%x",&a[i][j]); 9 for(int j=0;j<m;++j){ 10 scanf("%s",str); 11 for(int i=0;i<p;++i) 12 b[i][j]=str[i]-'0'; 13 } 14 btr=p/8+(p%8?1:0),ans=0;//p最多为64,将其分成p/8块,每块8个且有2^8=256种情况 15 for(int i=0;i<n;++i){//将A矩阵的列进行分块,预处理一下每块对应的256种情况 16 for(int j=0;j<btr;++j){//块数 17 for(int k=0;k<256;++k){//对应每块有0~255种情况 18 c[i][j][k]=0;//c[i][j][k]表示A矩阵中第i行第j块中第k种情况(二进制为k中bit位为1)的值为累加第i行第j块中bit为x对应的值 19 for(int x=0;x<8;++x) 20 if(k&(1<<x))c[i][j][k]+=a[i][j*8+x]; 21 } 22 } 23 } 24 for(int j=0;j<m;++j){//将矩阵B的行进行分块,统计每块中的每一列的二进制串代表的整数 25 for(int i=0;i<btr;++i){ 26 d[i][j]=0;//d[i][j]表示第i块第j列对应的整数 27 for(int k=0;k<8;++k) 28 d[i][j]+=b[i*8+k][j]<<k; 29 } 30 } 31 for(int i=0;i<n;++i){//利用预处理的结果,将对应的块中相乘的值加起来 32 for(int j=0;j<m;++j){ 33 tmp=0; 34 for(int k=0;k<btr;++k) 35 tmp+=c[i][k][d[k][j]]; 36 ans^=tmp; 37 } 38 } 39 printf("%d\n",ans); 40 } 41 return 0; 42 }
F.平衡二叉树
题目描述
平衡二叉树,顾名思义就是一棵“平衡”的二叉树。在这道题中,“平衡”的定义为,对于树中任意一个节点,都满足左右子树的高度差不超过 d. 空树的高度定义为0,单个节点的高度为1,其他情况下树的高度定义为根节点左右子树高度最大值 + 1. 一棵在高度上平衡的树,节点数可能不平衡,因此再定义一棵树的不平衡度为这棵树中所有节点的左右子树的节点数之差的最大值。
给定平衡的定义参数d, 你需要求出所有高度为 n 的平衡树中不平衡度的最大值。
给定平衡的定义参数d, 你需要求出所有高度为 n 的平衡树中不平衡度的最大值。
输入描述:
两个整数,n, d.
输出描述:
一个整数:所有高度为 n 的平衡树中不平衡度的最大值。
示例1
输入
4 1
输出
5
说明
下面这棵树在 d=1 的定义下高度是平衡的,其不平衡度为 5。
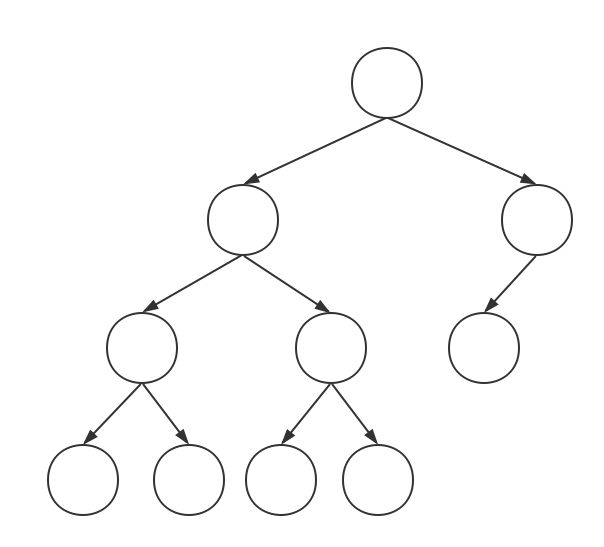
备注:
0 ≤ n, d ≤ 60.
解题思路:看代码。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL;LL n,d,dp[65]; 4 int main(){//dp[i]表示根节点的右子树中高度为i,平衡因子为d的当前节点所拥有的子节点(包括自己)的总个数 5 while(cin>>n>>d){ 6 memset(dp,0,sizeof(dp)); 7 for(LL i=1;i<=n-1-d;++i){//根节点的右子树最大高度为n-1-d,从右子树的叶子节点往上统计 8 if(i>d)dp[i]=dp[i-1]+dp[i-1-d]+1;//每层最多一个节点,如果当前节点的高度大于d,那么其包含节点的总个数为本身1+左子节点i-1拥有的节点数量+高度差为d右子节点i-1-d拥有的节点数量 9 else dp[i]=i;//否则为子节点的数量加上本身dp[i-1]+1即i 10 } 11 cout<<(1LL<<(n-1))-1-dp[max(n-1-d,0LL)]<<endl;//根节点的左子数为满二叉树 12 } 13 return 0; 14 }
H.卡牌游戏
题目描述
小贝喜欢玩卡牌游戏。某个游戏体系中共有N种卡牌,其中M种是稀有的。小贝每次和电脑对决获胜之后都会有一个抽卡机会,这时系统会随机从N种卡中选择一张给小贝。普通卡可能多次出现,而稀有卡牌不会被重复抽到。小贝希望收集到K种稀有卡牌,她想知道期望需要多少次获胜才能实现这个目标。
输入描述:
数据有多组,第一行一个整数T表示数据组数。
每组数据一行,三个整数N,M,K .
输出描述:
对于每组数据,输出形如"Case #x: y",其中 x 为这组数据的编号(从1开始),y 为这组数据的答案。答案的绝对误差或相对误差在10^(-6)以内都认为是正确的。
示例1
输入
2 5 2 1 40 9 5
输出
Case #1: 2.5 Case #2: 28.1146825397
备注:
1 ≤ T ≤ 100
1 ≤ N ≤ 10^5
1 ≤ M ≤ N
1 ≤ K ≤ M
解题思路:简单推导,假设第x次抽到稀有卡牌中的某一种(张),那么有x*m/n=1(1为只有一张),即x=n/m,那么总的期望次数就是∑j=0k-1(n-j)/(m-j)。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 int t,k;double ans,n,m; 5 int main(){ 6 while(cin>>t){ 7 for(int i=1;i<=t;++i){ 8 cin>>n>>m>>k;ans=0; 9 for(int j=0;j<k;++j)ans+=(n-j)/(m-j); 10 cout<<"Case #"<<i<<": "<<setiosflags(ios::fixed)<<setprecision(6)<<ans<<endl; 11 } 12 } 13 return 0; 14 }
Day_3
A.Knight
题目描述
有一张无限大的棋盘,你要将马从(0,0)移到(n,m)。
每一步中,如果马在(x,y),你可以将它移动到(x+1,y+2),(x+1,y-2),(x-1,y+2),(x-1,y-2),(x+2,y+1),(x+2,y-1),(x-2,y+1)或(x-2,y-1)。
你需要最小化移动步数。
每一步中,如果马在(x,y),你可以将它移动到(x+1,y+2),(x+1,y-2),(x-1,y+2),(x-1,y-2),(x+2,y+1),(x+2,y-1),(x-2,y+1)或(x-2,y-1)。
你需要最小化移动步数。
输入描述:
第一行一个整数t表示数据组数 (1≤ t≤ 1000)。
每组数据一行两个整数n,m (|n|,|m|≤ 10^9)。
输出描述:
每组数据输出一行一个整数表示最小步数。
示例1
输入
2 0 4 4 2
输出
2 2
解题思路:由于棋盘非常大,先bfs打表找一下规律。
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1005; 4 int t,n,m,cnt,mp[maxn][maxn],dir[8][2]={{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}}; 5 bool vis[maxn][maxn]; 6 struct node{int x,y,step;}nod; 7 queue<node> que; 8 void bfs(int x,int y){ 9 while(!que.empty())que.pop(); 10 memset(vis,false,sizeof(vis)); 11 mp[nod.x=x][nod.y=y]=nod.step=0;vis[x][y]=true; 12 que.push(nod); 13 while(!que.empty()){ 14 nod=que.front();que.pop(); 15 if(!nod.x&&!nod.y){cout<<nod.step<<endl;return;} 16 for(int i=0;i<8;++i){ 17 node next=nod; 18 next.x+=dir[i][0]; 19 next.y+=dir[i][1]; 20 next.step++; 21 if(!next.x&&!next.y){cout<<next.step<<endl;return;} 22 if(next.x>=0&&next.y>=0&&next.x<61&&next.y<61&&!vis[next.x][next.y]){ 23 vis[next.x][next.y]=true; 24 mp[next.x][next.y]=next.step; 25 que.push(next); 26 } 27 } 28 } 29 } 30 int main(){ 31 while(cin>>t){ 32 while(t--){ 33 cin>>n>>m; 34 bfs(n,m); 35 for(int i=0;i<n+m;++i) 36 for(int j=0;j<n+m;++j) 37 cout<<mp[i][j]<<(j==n+m-1?'\n':' '); 38 } 39 } 40 return 0; 41 }
打完表之后发现数据是成中心对称的,且第一象限内又关于直线y=x对称,所以预处理一下½的数据即可,如图:

由图可知:在直线L2下面部分,每个数字都有4层,而夹在直线L1和直线L2之间的数据只有3层,除了两个特殊的坐标点外:(1,0)---> 3步、(2,1)---> 4步,手推找规律:①当点(n,m)(n始终处理成大于或等于m)在直线L2下面包括在直线L2上时,即m≤n/2 ---> 2*m≤n,step=n-m-2*floor((n-2*m)/4.0);②当点(n,m)(n始终处理成大于或等于m)处在直线L1和直线L2之间时,即2*m>n,step=n-m-2*floor((n-2*m)/3.0)。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 int t,n,m,step; 4 int main(){ 5 while(cin>>t){ 6 while(t--){ 7 cin>>n>>m; 8 n=abs(n),m=abs(m);step=0; 9 if(n<m)swap(n,m);//处理为第一象限的1/2部分 10 if(n==1&&!m)step=3; 11 else if(n==2&&m==2)step=4; 12 else{ 13 if(2*m>n)step=n-m-2*floor((n-2*m)/3.0); 14 else step=n-m-2*floor((n-2*m)/4.0); 15 } 16 cout<<step<<endl; 17 } 18 } 19 return 0; 20 }
D.Shopping
题目描述
你要买n件物品,其中有一些是凳子。
商场正在举行促销活动,如果购物车中有至少一个凳子,那么你可以半价购买这个购物车中最贵的一个物品。
你有m辆购物车,请最小化你的花费。
商场正在举行促销活动,如果购物车中有至少一个凳子,那么你可以半价购买这个购物车中最贵的一个物品。
你有m辆购物车,请最小化你的花费。
输入描述:
第一行一个整数t表示数据组数 (1 ≤ t ≤ 100)。
每组数据第一行两个整数n,m (1 ≤ n,m ≤ 1000),接下来n行每行两个整数a_i,b_i,分别表示第i件物品的价格以及它是否是凳子 (1 ≤ a_i ≤ 10^5, 0 ≤ b_i ≤ 1)。
输出描述:
每组数据输出一行一个实数表示最小花费,保留一位小数。
示例1
输入
2 5 1 1 0 2 1 3 1 4 0 5 0 5 10 1 0 2 1 3 1 4 0 5 0
输出
12.5 10.5
解题思路:将物品价格从小到大排序,从后往前取min(num,m)个物品的一半价格+剩下物品的总价格即可。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const int maxn=1e5+5; 5 int t,n,m,num,a[maxn],b;double sum; 6 int main(){ 7 while(cin>>t){ 8 while(t--){ 9 cin>>n>>m;num=0;sum=0.0; 10 for(int i=0;i<n;++i){ 11 cin>>a[i]>>b; 12 if(b)num++; 13 sum+=a[i]; 14 } 15 sort(a,a+n); 16 for(int i=1;i<=num&&i<=m;++i)sum-=a[n-i]/2.0; 17 cout<<setiosflags(ios::fixed)<<setprecision(1)<<sum<<endl; 18 } 19 } 20 return 0; 21 }
H.Travel
题目描述
魔方国有n座城市,编号为1~n。城市之间通过n-1条无向道路连接,形成一个树形结构。
澜澜打算在魔方国进行m次旅游,每次游览至少一座城市。为了方便,每次旅游游览的城市必须是连通的。此外,澜澜希望游览所有城市恰好一次。
澜澜想知道有多少种旅游方案满足条件,两个方案不同当且仅当存在某一次旅游游览了不同的城市。
澜澜不会数数,所以只好让你来帮他数方案。
澜澜打算在魔方国进行m次旅游,每次游览至少一座城市。为了方便,每次旅游游览的城市必须是连通的。此外,澜澜希望游览所有城市恰好一次。
澜澜想知道有多少种旅游方案满足条件,两个方案不同当且仅当存在某一次旅游游览了不同的城市。
澜澜不会数数,所以只好让你来帮他数方案。
输入描述:
第一行一个整数t表示数据组数 (1 ≤ t ≤ 100)。
每组数据第一行两个整数n,m (1 ≤ m ≤ n ≤ 10^5, ∑n ≤ 10^6),接下来n-1行每行两个整数a_i,b_i表示一条道路 (1≤ a_i,b_i ≤ n)。
输出描述:
每组数据输出一行一个整数表示方案数对1e9+7取模的结果。
示例1
输入
2 3 1 1 2 1 3 3 2 1 2 1 3
输出
1 4
解题思路:澜澜将在魔方国中进行m次旅行,要求魔方国的n座城市恰好全部被浏览一次,这就相当于在n-1个空中放m-1块隔板将n座城市划分成m块,由于块与块之间浏览的次序不同造成更多的方案数,因此还需乘上m!。公式:C(n-1,m-1)*m!%mod。组合数取模大质数-->乘法逆元+费马小定理快速求解即可。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const LL mod=1e9+7; 5 const int maxn=1e5+5; 6 LL t,n,m,a,b,fac[maxn]={1}; 7 LL quick_pow(LL a,LL b,LL mod){ 8 LL ans=1; 9 while(b){ 10 if(b&1)ans=ans*a%mod; 11 a=a*a%mod; 12 b>>=1; 13 } 14 return ans; 15 } 16 int main(){ 17 for(LL i=1;i<maxn;++i)fac[i]=fac[i-1]*i%mod; 18 while(cin>>t){ 19 while(t--){ 20 cin>>n>>m; 21 for(int i=1;i<n;++i)cin>>a>>b; 22 cout<<fac[m]*fac[n-1]%mod*quick_pow(fac[m-1]*fac[n-m]%mod,mod-2,mod)%mod<<endl; 23 } 24 } 25 return 0; 26 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号