20182304张子正 2020-2021-2 Python综合实践

20182304张子正 2020-2021-2 Python综合实践

课程：《Python程序设计》
班级： 1823
姓名： 张子正
学号：20182304
实验教师：王志强
实验日期：2021年6月24日
必修/选修： 公选课

1.实验内容

• Python综合应用：我选择了神经网络算法
• 所谓神经网络的训练或者是学习，其主要目的在于通过学习算法得到神经网络解决指定问题所需的参数，这里的参数包括各层神经元之间的连接权重以及偏置等。因为作为算法的设计者（我们），我们通常是根据实际问题来构造出网络结构，参数的确定则需要神经网络通过训练样本和学习算法来迭代找到最优参数组。
• 说起神经网络的学习算法，不得不提其中最杰出、最成功的代表——误差逆传播（error BackPropagation，简称BP）算法。BP学习算法通常用在最为广泛使用的多层前馈神经网络中。

2.神经网络反向传播原理

backpropagation算法步骤

• BP算法的主要流程可以总结如下：
• 输入：训练集D=(xk,yk)mk=1D=(xk,yk)k=1m; 学习率;
• 过程：
  1. 在(0, 1)范围内随机初始化网络中所有连接权和阈值
  2. repeat:
  3. for all (xk,yk)∈D(xk,yk)∈D do
  4. 根据当前参数计算当前样本的输出;
  5. 计算输出层神经元的梯度项；
  6. 计算隐层神经元的梯度项；
  7. 更新连接权与阈值
  8. end for
  9. until 达到停止条件
• 输出：连接权与阈值确定的多层前馈神经网络
  

softmax函数

• SoftMax顾名思义就是取max以一种soft的方式，与之对应的就是hardmax，hardmax最大的特点就是只选出其中一个最大的值，而Softmax的区别就在于不再唯一的确定某一个最大值，而是为每个输出分类的结果都赋予一个概率值，表示属于每个类别的可能性。
  softMax的结果相当于输入图像被分到每个标签的概率分布，该函数是单调增函数，即输入值越大，输出也就越大，输入属于该标签的概率就越大。
  

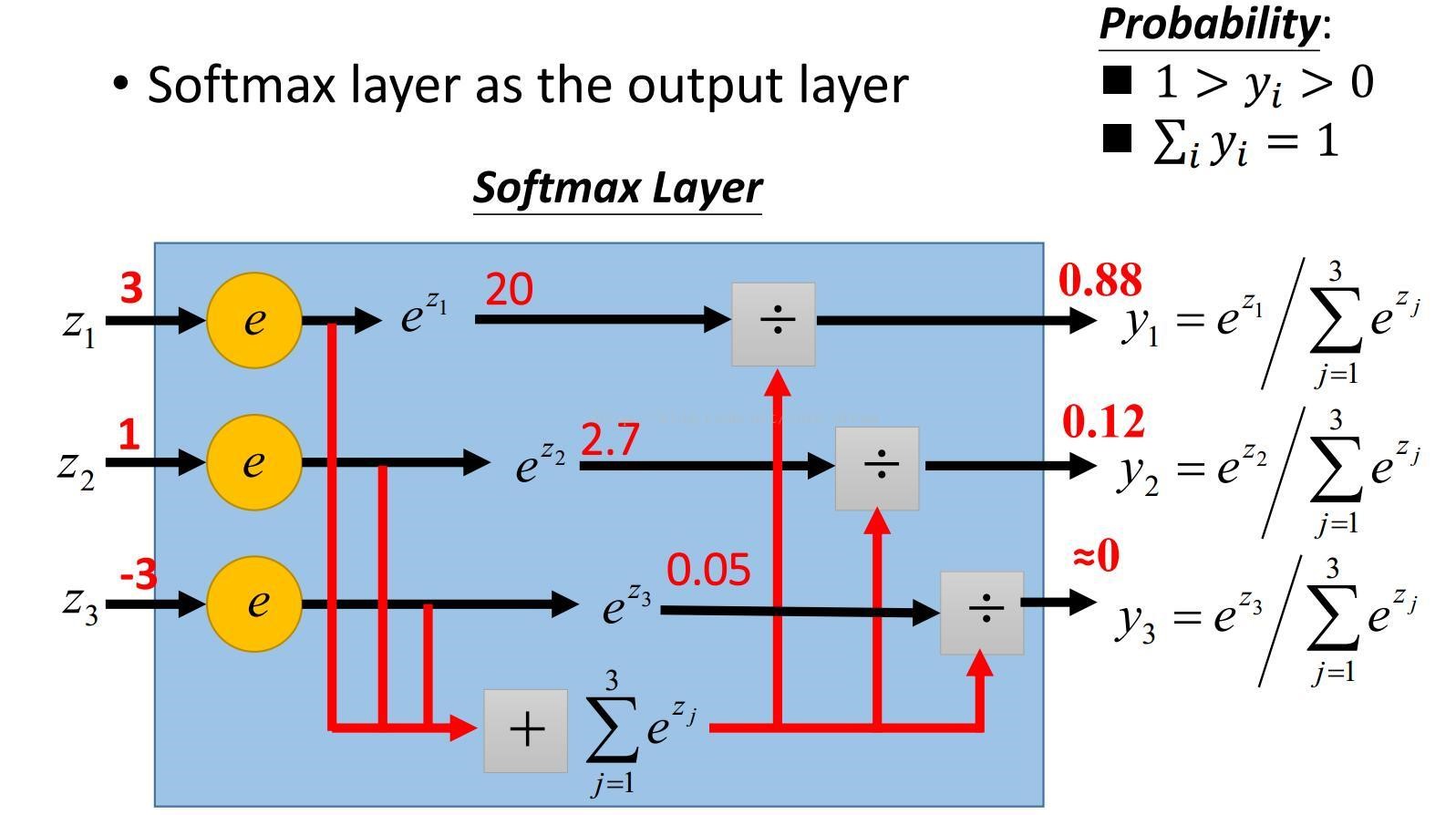
• 对softmax的结果计算交叉熵分类损失函数为：
  

• 上面已经说到softmax其实是一个概率，是正确类别对应输出节点的概率值，那么我们当然希望这个概率越大越好。

• 但是这个带有指数函数不好进行求导等运算，于是取log，log是单增函数，不改变单调性，再添上负号就变成了损失函数，将求最大值问题转换为求负的最小值问题，即max F()—->min -F()。我们希望的是损失函数越小越好，推出loss函数如下：
  

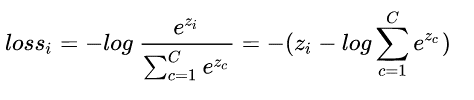
• 取log里面的值就是这组数据正确分类的Softmax值，损失函数越大，说明该分类器在真实标签上的分类概率越小，性能也就越差，反之，性能就越好。

3.代码设计思路

搭建神经网络

• 定义模型结构、初始化模型参数。函数的主要作用就是初始化，通过输入的变量（输入、隐藏层和输出层size）来确定神经网络的规模大小，同时通过random函数初始化隐藏层和输出层的权重与偏倚参数。

# set the number of iterations
num_iterations = 200000
# set the number of learning_rate
learning_rate = 0.01

input_size = 28 * 28
output_size = 10
hidden_size = 300

model = Network(input_size, hidden_size, output_size)
model.train(x_train,
            y_train,
            Num_iterations=num_iterations,
            Learning_rate=learning_rate)

print("Accuracy: {}".format(model.testing(x_test, y_test)))

计算当前损失（正向传播）

• 正向传播是从输入层---->隐含层、隐含层---->输出层，即把网络正向的走一遍：输入层、隐藏层、输出层，计算每个结点对其下一层结点的影响。根据输入以及各层值之间的参数矩阵，通过向量点乘（加权求和）进行前向传播，使用激活函数，并且计算了网络的loss值。现在与实际值相差还很远，现在我们对误差进行反向传播，更新权值，重新计算输出。
• Z:是利用公式计算隐藏层的净输入I1,就是w1x1···+b的那个结果。
• H:Sigmoid、把输出结果Z压缩在[0,1]之间。
• U：利用公式，计算输出层的净输入I2，于是得到后向传播的思路：构造y-hat函数，得到梯度。
• 之后再利用softmax函数得到predict_list，使用-log得到loss，也就是损失函数(见上图)，最后返回f_result数组，方便使用。
  
  

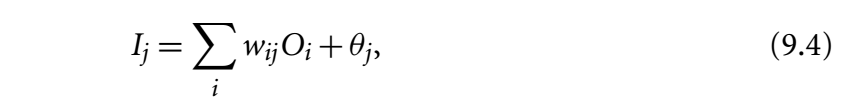
def forward(self, x, y):
    Z = np.matmul(self.w1, x).reshape((self.hidden_size, 1)) + self.b1
    H = np.maximum(Z, 0)
    U = np.matmul(self.w2, H).reshape((self.output_size, 1)) + self.b2

    predict_list = 1 / sum(np.exp(U)) * np.exp(U)
    loss = -np.log(predict_list[y]).item()
    f_result = {
        'Z': Z,
        'H': H,
        'U': U,
        'f_x': predict_list.reshape((1, self.output_size)),
        'error': loss
    }
    return f_result

计算当前梯度（反向传播）

• 正向传播过程结束后，这时输出结果一般离目标值差距很远。这个时候就需要比较输出和实际结果之间的差异，将残差返回给整个网络，调整网络中的权重关系，更新权值，首先是隐藏层---->输出层的权值更新，如果我们想知道权重参数对整体误差产生了多少影响，可以用整体误差对权重参数求偏导求出，然后来更新权重参数的值，然后是隐含层---->隐含层的权值更新。通过调整输入节点与隐藏节点的权重参数和隐藏节点与输出节点的权重参数以及临界值，使误差沿梯度方向下降。最后创建一个字典grad，保存dw和db。

def back_propagation(self, x, y, f_result):
    E = np.array([0] * self.output_size).reshape((1, self.output_size))
    E[0][y] = 1
    dU = (-(E - f_result['f_x'])).reshape((self.output_size, 1))
    db2 = copy.copy(dU)
    dw2 = np.matmul(dU, f_result['H'].transpose())
    delta = np.matmul(self.w2.transpose(), dU)
    db1 = delta.reshape(self.hidden_size, 1) * (f_result['Z'] > 0).reshape(self.hidden_size, 1)
    dw1 = np.matmul(db1.reshape((self.hidden_size, 1)), x.reshape((1, 784)))

    grad = {
        'dw2': dw2,
        'db2': db2,
        'db1': db1,
        'dw1': dw1
    }
    return grad

更新参数（梯度下降）

• 构造一个y-hat函数E，将输出层输出softmax后的结果predict_list减去y-hat，得到dU
• 根据链式求导法则得到相应更新。这一步直接根据学习率来更新权重,就是对w和b做一个值的更新。

def back_propagation(self, x, y, f_result):
    E = np.array([0] * self.output_size).reshape((1, self.output_size))
    E[0][y] = 1
    dU = (-(E - f_result['f_x'])).reshape((self.output_size, 1))
    db2 = copy.copy(dU)
    dw2 = np.matmul(dU, f_result['H'].transpose())
    delta = np.matmul(self.w2.transpose(), dU)
    db1 = delta.reshape(self.hidden_size, 1) * (f_result['Z'] > 0).reshape(self.hidden_size, 1)
    dw1 = np.matmul(db1.reshape((self.hidden_size, 1)), x.reshape((1, 784)))

    grad = {
        'dw2': dw2,
        'db2': db2,
        'db1': db1,
        'dw1': dw1
    }
    return grad

train训练函数

• 绘制loss与准确率关于迭代次数（count）的图像：首先定义两个空数组funtest=[]与funloss=[]分别作为y轴，xdemin作为x轴（ ，并且步长为5000），每5000次取当前test和loss的函数值，用append函数将值加在funtest和funloss数组的末尾，最后使用pyplot绘图。

def train(self,X_train,Y_train,num_iterations = 1000,learning_rate = 0.5):
    rand_indices = np.random.choice(len(X_train),num_iterations,replace=True)
    count = 1
    maxtest=0.0
    maxindex=0.0
    funtest=[]
    funloss=[]
    for i in rand_indices:
        f_result = self.forward(X_train[i],Y_train[i])
        b_result = self.back_propagation(X_train[i],Y_train[i],f_result)
        self.optimize(b_result,lr_adjust(learning_rate,i,num_iterations))
        elem= self.testing(x_test,y_test)
        if format(elem) > str(maxtest):
            maxtest=format(elem)
            maxindex=format(count)
        if count % 1000 == 0:
            if count % 5000 == 0:
                test = self.testing(x_test,y_test)
                funtest.append(test)
                funloss.append(f_result['error'])
                xdemin =np.linspace(5000,200000,40)
                #xdemin=range(5000,20000,5000)
                print('Trained for {} times,'.format(count),'test = {}'.format(test))
                print(f_result['error'])
                if format(test) > str(maxtest):
                    maxtest=format(test)
                    maxindex=format(count)
            else:
                print('Trained for {} times.'.format(count))
        count += 1
    print('Training finished!')
    print(maxtest)
    print(maxindex)
    plt.figure()
    plt.plot(xdemin, funtest, linewidth=3, linestyle='dotted')
    plt.show()

    plt.figure()
    plt.plot(xdemin, funloss, linewidth=3, linestyle='dotted')
    plt.show()

测试函数

• 测试测试集并得到准确率。定义变量总正确数total_correct，每当模型输出的结果与正确值相同就加1，最后返回正确率total_correct / len(X_test)。

def testing(self, X_test, Y_test):
    total_correct = 0
    for n in range(len(X_test)):
        y = Y_test[n]
        x = X_test[n][:]
        prediction = np.argmax(self.forward(x, y)['f_x'])
        if prediction == y:
            total_correct += 1

    return total_correct / len(X_test)

4.实验结果

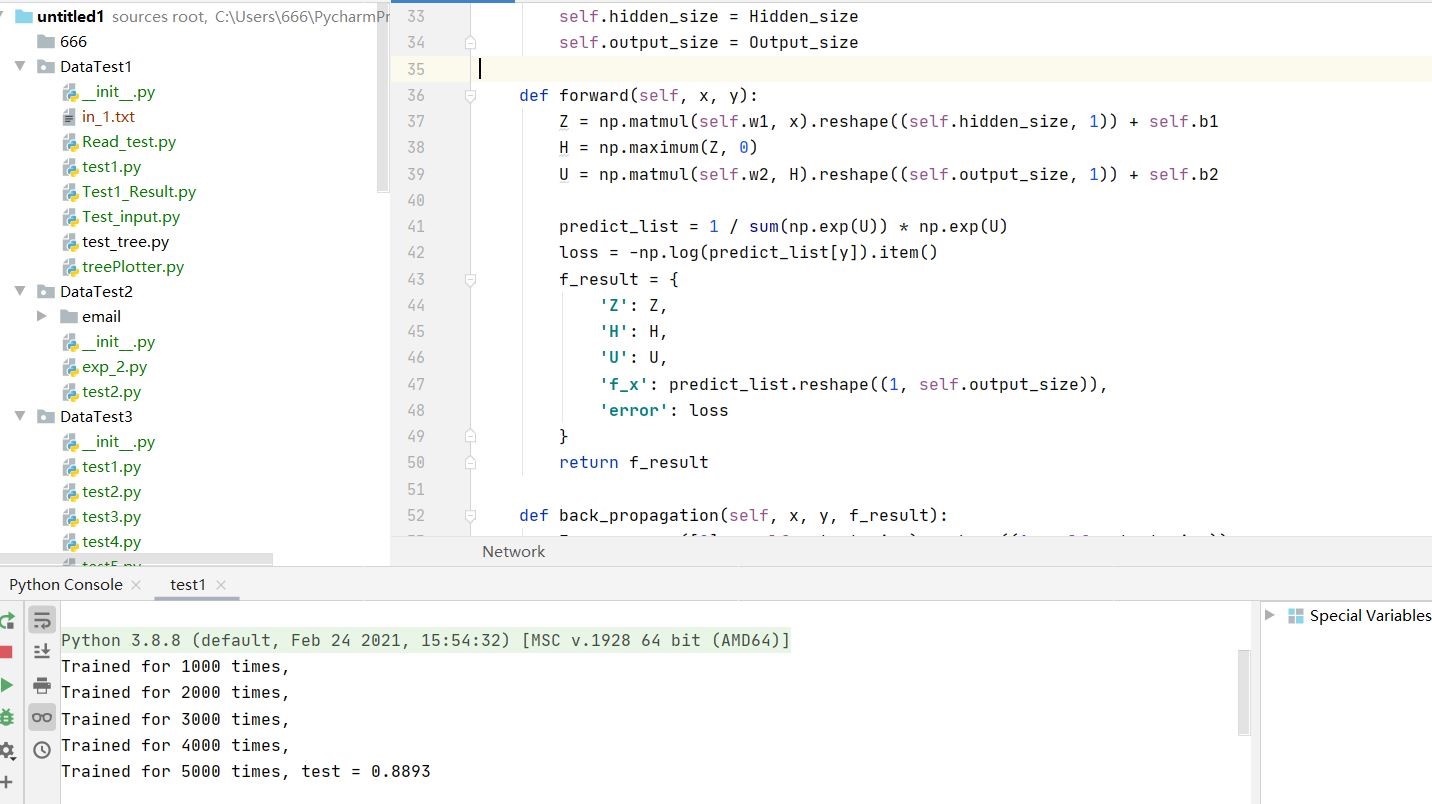
Trained for 1000 times,
Trained for 2000 times,
Trained for 3000 times,
Trained for 4000 times,
Trained for 5000 times, test = 0.8973
Trained for 6000 times,
Trained for 7000 times,
Trained for 8000 times,
Trained for 9000 times,
Trained for 10000 times, test = 0.9061
Trained for 11000 times,
Trained for 12000 times,
Trained for 13000 times,
Trained for 14000 times,
Trained for 15000 times, test = 0.9269
Trained for 16000 times,
Trained for 17000 times,
Trained for 18000 times,
Trained for 19000 times,
Trained for 20000 times, test = 0.9324
Trained for 25000 times, test = 0.9391
Trained for 30000 times, test = 0.9455
Trained for 35000 times, test = 0.9423
Trained for 40000 times, test = 0.9421
Trained for 45000 times, test = 0.9534
Trained for 50000 times, test = 0.9565
Trained for 55000 times, test = 0.9628
Trained for 60000 times, test = 0.9619
Trained for 65000 times, test = 0.9599
Trained for 70000 times, test = 0.9671
Trained for 75000 times, test = 0.9634
Trained for 80000 times, test = 0.9653
Trained for 85000 times, test = 0.9598
Trained for 90000 times, test = 0.9692
Trained for 95000 times, test = 0.9634
Trained for 96000 times,
Trained for 97000 times,
Trained for 98000 times,
Trained for 99000 times,
Trained for 100000 times, test = 0.9686
Trained for 105000 times, test = 0.9689
Trained for 110000 times, test = 0.9691
Trained for 115000 times, test = 0.9702
Trained for 120000 times, test = 0.9726
Trained for 125000 times, test = 0.9667
Trained for 130000 times, test = 0.9692
Trained for 135000 times, test = 0.9638
Trained for 140000 times, test = 0.971
Trained for 145000 times, test = 0.972
Trained for 150000 times, test = 0.9681
Trained for 155000 times, test = 0.9746
Trained for 160000 times, test = 0.9687
Trained for 165000 times, test = 0.9751
Trained for 170000 times, test = 0.9734
Trained for 175000 times, test = 0.9692
Trained for 180000 times, test = 0.9743
Trained for 185000 times, test = 0.9734
Trained for 190000 times, test = 0.9719
Trained for 195000 times, test = 0.9735
Trained for 200000 times, test = 0.9753
Training finished!
Accuracy: 0.9753

• 根据实验结果，训练后得到的模型准确度为97.53%，大于93%，训练模型精确度较高。

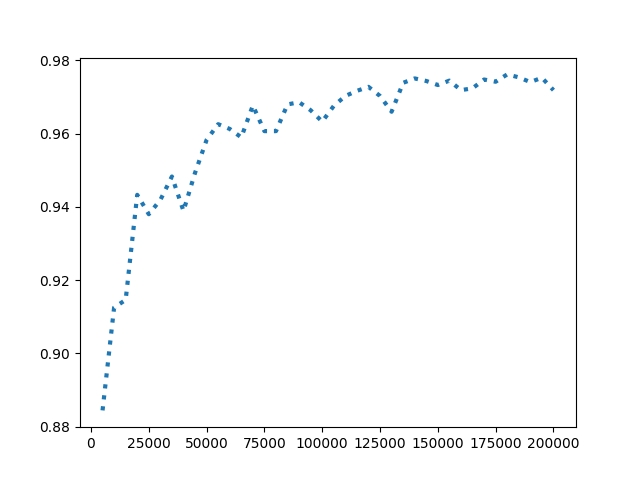
• 准确率随迭代次数的递增整体呈上升趋势，说明模型经过训练后愈发精确，但也伴随着震荡。
  
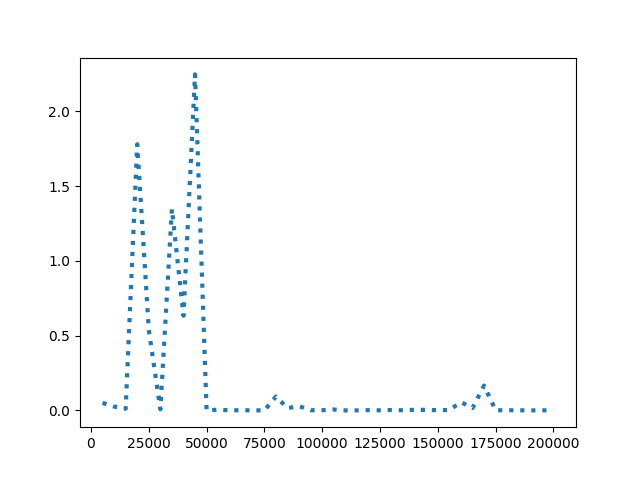
• loss函数的值先震荡后趋于稳定，且趋近于0。由前文可知loss越小代表损失值越小，即softmax值越大，输入对应的输出结果与事实相同的概率越高，即模型拟合越好。

上传码云

• 码云链接

5. 大作业感想

• 本次大作业难度非常大，首先难度在于神经网络反向传播的具体计算。其实可以把神经网络输入层、隐藏层、输出层都带上值去算一下，前向传播算法基本就是权值乘起来，相对比较好理解。但是计算出来误差很大，就要用反向传播来纠偏，首先计算总误差，主要是通过链式法则求偏导数，这个过程的数学计算比较复杂，公式很多，体现在代码上也很复杂。然后隐含层---->隐含层的权值更新会接受来自多方面的误差，之后最后我们再把更新的权值重新计算，不停地迭代，最后准确度会越来越高。我通过参考学习网上大量的相应资料以及博客，才能顺利完成作业。很多博客确实分析的不错，从代码和原理两方面进行了阐释，我把博客链接放到了最后。

6.课程感想体会、意见和建议

• 经过一个学期的Python课程学习，我的收获非常大。我之前上过王老师的课程，对于王老师的讲课风格也比较熟悉。王老师上课干货还是很多的，一学期讲了不少内容，从基本语法到爬虫、表格操作等高级的内容都有涉猎。我发现Python基础语法并不复杂，而且功能非常强大，在机械学习，数据挖掘等领域应用广泛。但是我在实践编程时还是遇到了很多困难，很多时候对于代码的整体结构还不是非常熟悉，还总犯一些基础性错误。编程是一门实践课程，离不开一点一点的调试程序，我也在反思这学期在编程方面下的功夫不够。在PYthon课上，我也看到了很多优秀的学弟学妹，能力非常强，这对我也是一种激励与挑战，希望大家能一起提升技术水平，增强编程应用能力。感谢王老师一学期的辛勤付出！
• 我也稍微提一点意见和建议：希望老师可以把教室固定在有电源插座的实验室，我在好几节课上电脑撑不住，没电了，影响了上课的编程学习。还有就是老师能不能推出一些编程进阶课程，把爬虫、表格操作、数据库往深了讲一讲。

7.参考资料

• 深度学习笔记(一):实现一个神经网络算法
• 一文弄懂神经网络中的反向传播法——BackPropagation
• 吴恩达B站视频