《数据结构与面向对象程序设计》第十周学习总结
学号20182304 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
教材学习内容总结
- 图是跟一般的树的概念所区分,它不约束除根节点外的每一个顶点有且只能有一个父节点。图中没有根,每个顶点都能与最多n-1个其它节点相连。
- 邻接:两个顶点之间有一条边,则称这两个顶点是邻接的
- 路径:连接两个顶点之间的一系列边称为两个顶点间的路径,边的条数称为路径长度
- 环路:首顶点与末顶点相同且路径中没有边重复的路径
- 点的入度:以点为终点的有向边数
- 点的出度:以点为起点的有向边数
- 图可以根据是否具有方向分为两种:有向图和无向图
- 无向图:在图中若任意两个顶点的边为无向边,则称该图为无向图
- 有向图:在图中所有边为有向边,便是有向图
- 有序通常用尖括号表示,无序通常用圆括号表示
- 图也可以根据每条边是否带有权重分为加权图和网络,可以根据边或弧的多少分为稠密图和稀疏图,生成树是一种特殊的图
- 生成树:包含无向图所有顶点的极小联通子图
- 图的表示:
- 邻接表:邻接表,存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中
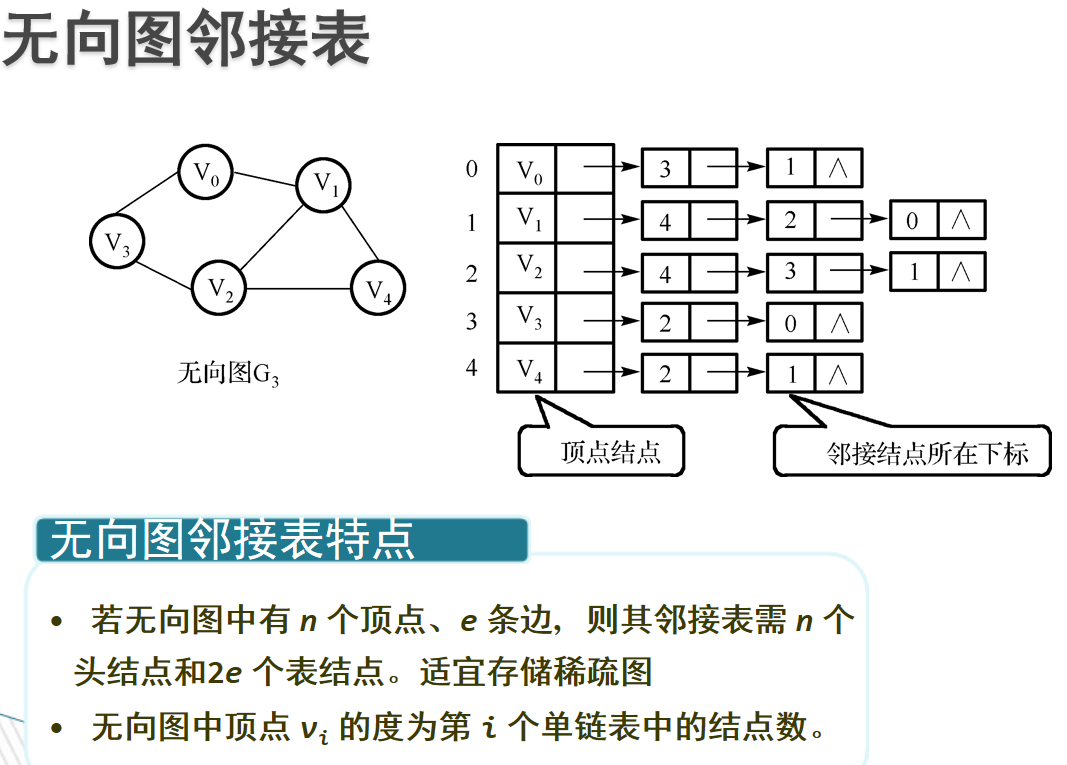
- 邻接表:邻接表,存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中

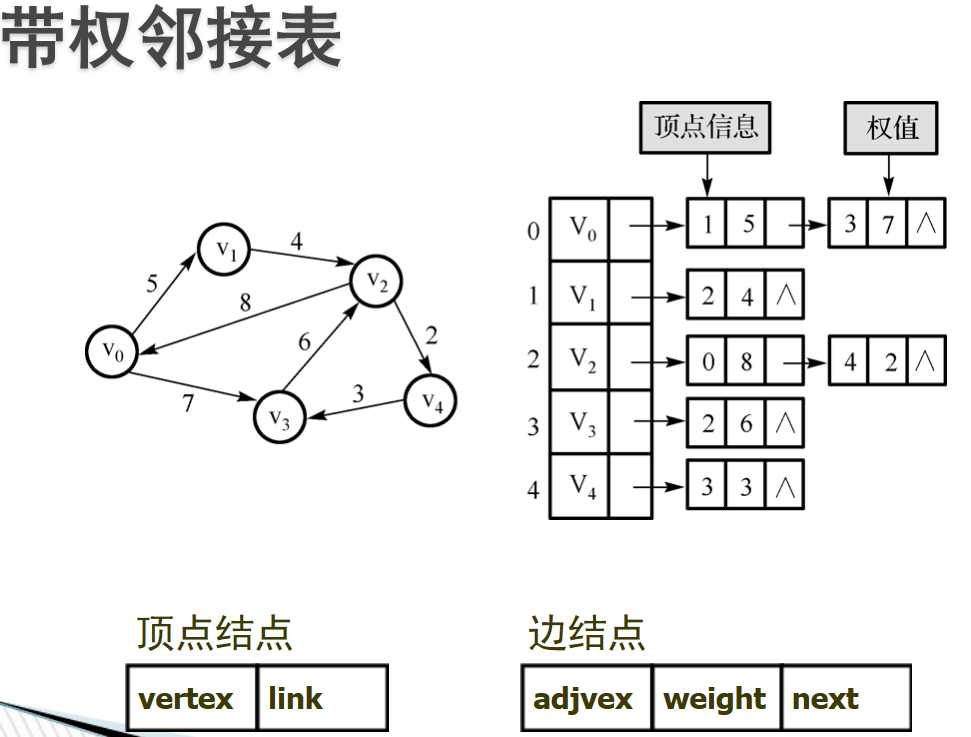
- 邻接矩阵:邻接矩阵:利用一个二维数组实现的矩阵,行列的元素代表顶点,而矩阵中的元素代表边
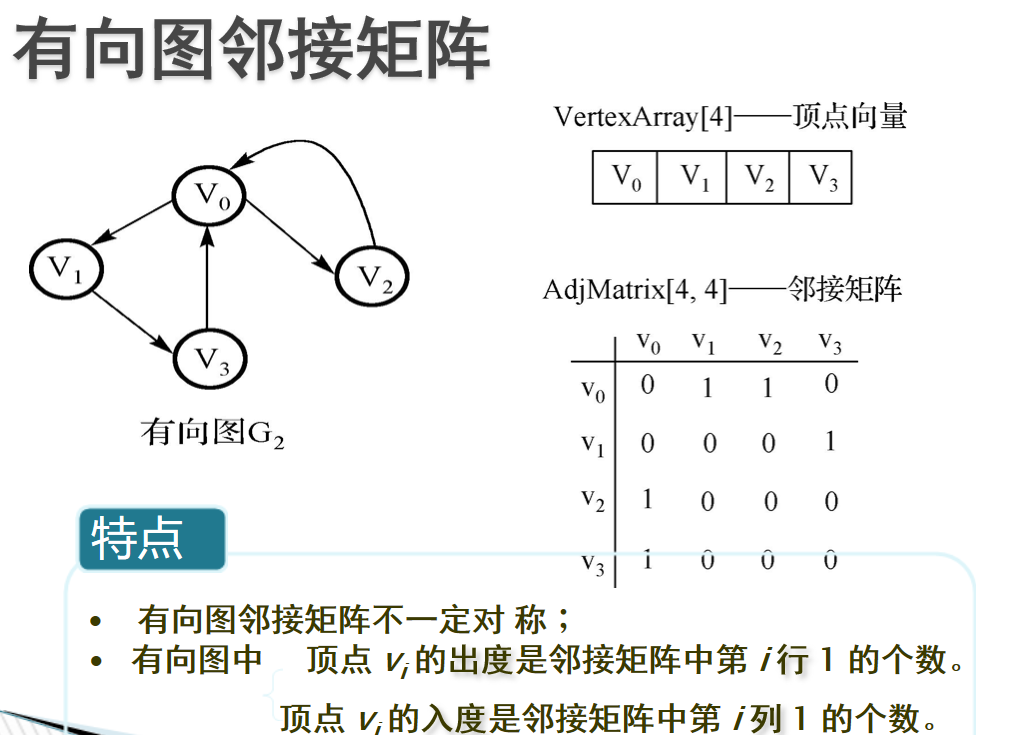
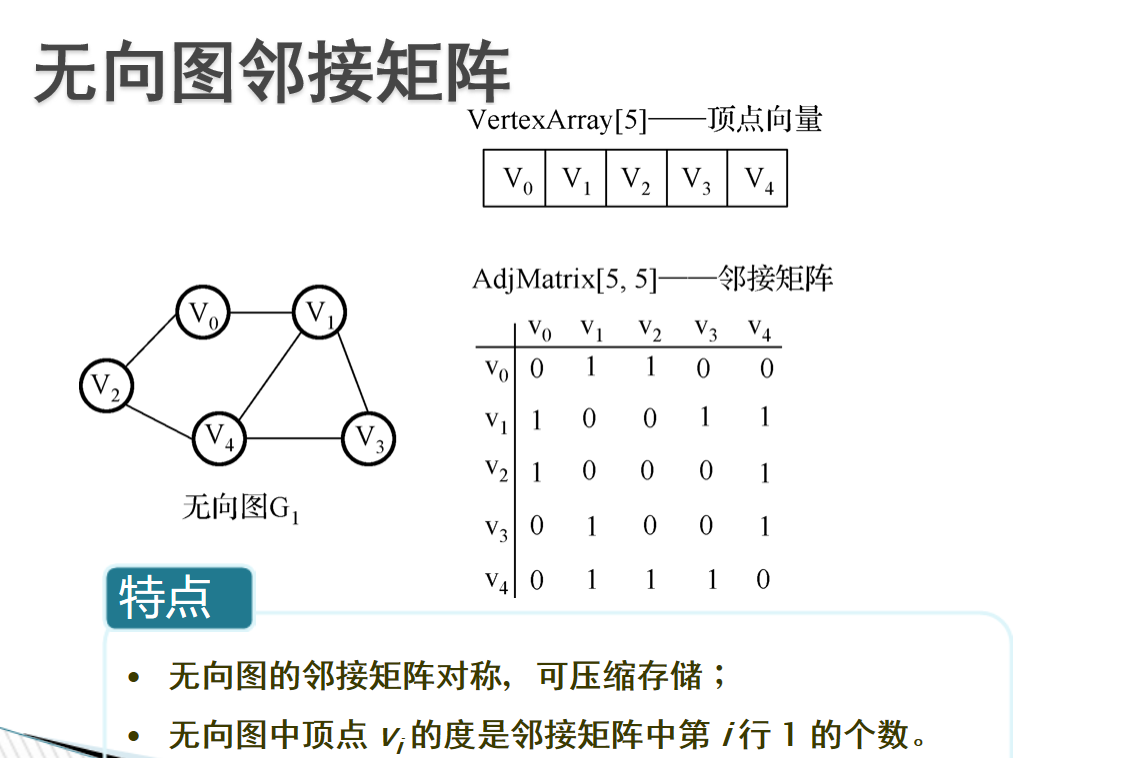

-
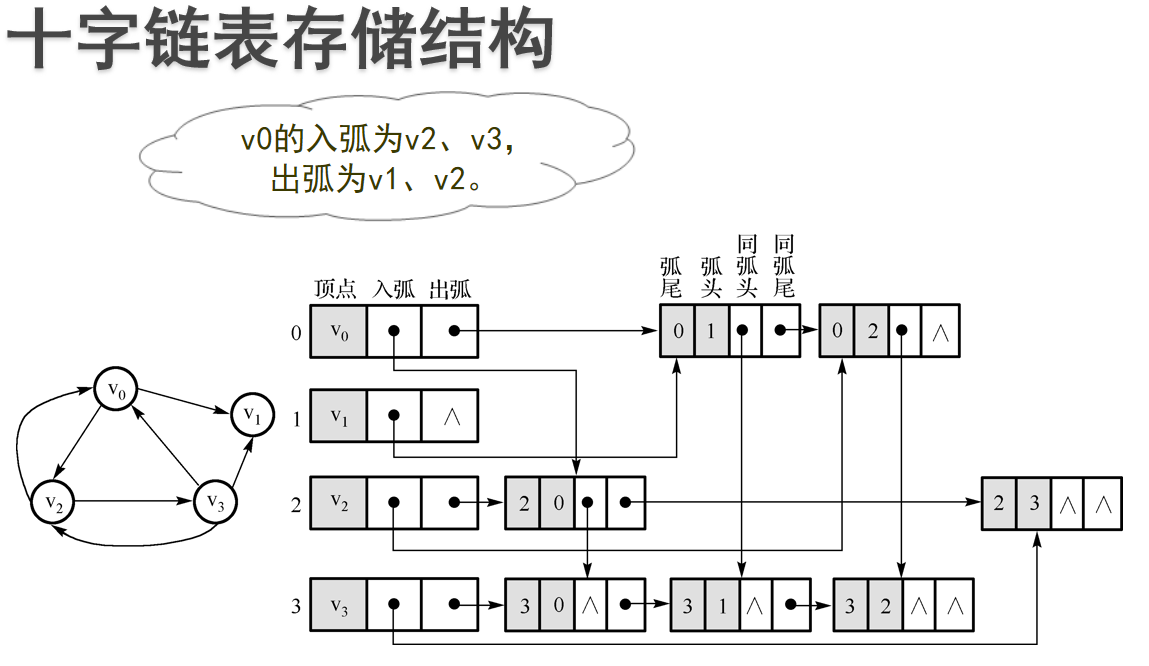
十字链表:十字链表(Orthogonal List)是有向图的另一种链式存储结构。该结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的
-
图的遍历:
-
广度优先遍历:像石头落在水里激起的涟漪一样,一层一层的遍历
-
BFS算法之所以叫做广度优先搜索,是因为它始终将已发现的顶点和未发现的之间的边界,沿其广度方向向外扩展。亦即,算法首先会发现和s距离为k的所有顶点,然后才会发现和s距离为k+1的其他顶点。同深度优先搜索相反,BFS宽度优先搜索每次选择深度最浅的节点优先扩展。并且当问题有解时,宽度优先算法一定能够找到解,并且在单位耗散时间的情况下,可以保证找到最优解。
-
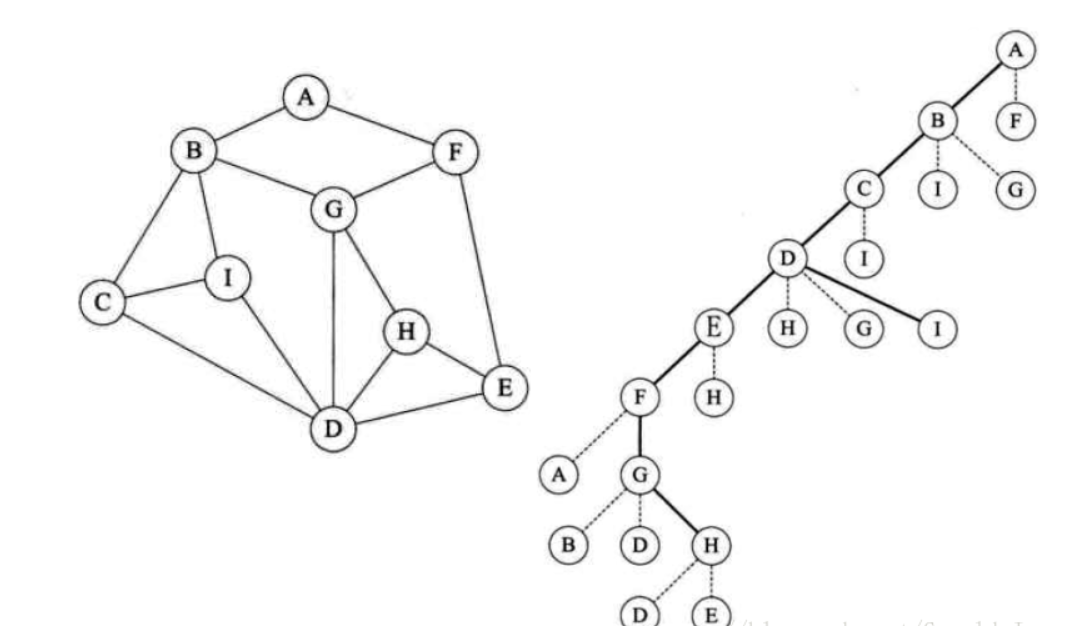
深度优先遍历:深度优先遍历,顾名思义即为一条道走到黑的搜索策略,行不通退回来换另外一条道再走到黑,依次直到搜索完成。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。可以通过图示清晰的说明。假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
-
-
图的最小生成树:个有n个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有n个结点,并且有保持图连通的权值和边最小
教材学习中的问题和解决过程
- 问题1:如何简要理解拓扑算法
- 问题1解决方案::类似于二叉树的层次遍历,遍历所有结点,将入度为0的结点存在一个栈中,依次输出栈内的各个结点时,将每个节点的子节点的度减1,然后将其中度为0的结点存入栈中,循环执行上述操作,直到所有结点遍历完。
- 问题2:如何理解和绘制十字链表
- 问题2解决方案:首先明确一些概念

- 入弧和出弧:入弧表示图中发出箭头的顶点,出弧表示箭头指向的顶点
- 弧头和弧尾:弧尾表示图中发出箭头的顶点,弧头表示箭头指向的顶点
- 同弧头和同弧尾:同弧头,弧头相同弧尾不同;同弧尾,弧头不同互为相同
具体绘制过程: - 第一步,列出图的所有顶点,并进行编号。每行含三个方格的横格,顶点那栏分别填写各顶点,入弧和出弧的暂时不管
- 第二步,画出各行对应的顶点表示出弧的所有关系。画的时候为了方便之后的连线,建议可以将弧尾相同的画在同一行,将弧头相同的画同一列。填写弧尾与弧头,同弧头和同弧尾先暂时不管。
- 第三步,连线。将表示顶点的三格图中入弧指向对应列所有的四格方格。四格方格中,同弧头指向本列,同弧尾指向本行。若出弧或同弧尾右边没有方格,则为空。
- 问题3:DFS和BFS算法比较,各自有什么特点和应用场景
- 问题3解决方案:
- DFS深度优先搜索,空间需求较低,不需要BFS需要一个队列保存搜索过程中搜索记录;其次,深搜在搜索过程中要考虑回溯,在搜索HTML链接,爬取数据方面适用颇多;多用于解决连通性问题。
- BFS广度优先搜索,空间需求较高,根据其搜索模式,因为是按层进行搜索,所以很容易求得最短路径。可以应用于Dijkstral和prim算法
代码调试中的问题和解决过程
-
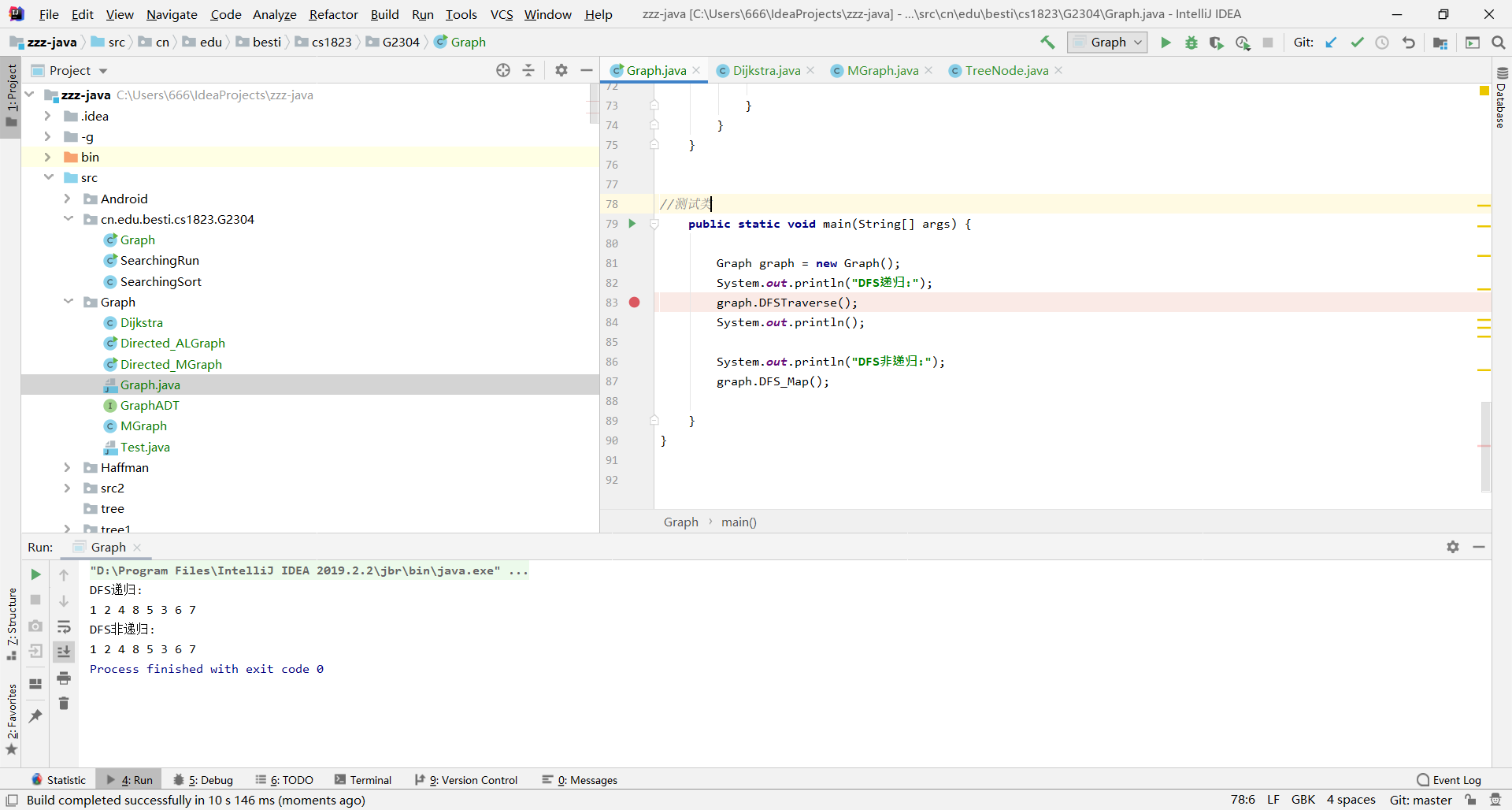
问题1:如何用Java具体实现深度遍历
-
问题1解决方案:具体实现如下。只要建立邻接矩阵和对应的标志数组,就可以相对容易的实现。DFS利用递归来实现比较易懂,DFS非递归就是将需要的递归的元素利用一个栈Stack来实现,以达到递归时候的顺序。
import java.util.Stack;
public class Graph {
//节点个数
private static int number = 8;
//创立访问标志数组的布尔型数组
private boolean[] flag;
//创立要遍历节点的数组
private int[] num= {1,2,3,4,5,6,7,8};
//创立这几个数字的邻接矩阵
private int[][] edges = {
{0, 1, 1, 0, 0, 0, 0, 0},
{1, 0, 0, 1, 1, 0, 0, 0},
{1, 0, 0, 0, 0, 1, 1, 0},
{0, 1, 0, 0, 0, 0, 0, 1},
{0, 1, 0, 0, 0, 0, 0, 1},
{0, 0, 1, 0, 0, 0, 1, 0},
{0, 0, 1, 0, 0, 1, 0, 0},
{0, 0, 0, 1, 1, 0, 0, 0},
};
void DFSTraverse() {
//设置一个和数字个数同等大小的布尔数组
flag = new boolean[number] ;
//从顶点开始,实现深度遍历
for (int i = 0; i < number; i++) {
if (flag[i] == false) {
// 如果当前顶点没有被访问,进入DFS
DFS(i);
}
}
}
//完成一次遍历,直到后面无连接节点
void DFS(int i) {
// 标记第num[i]个节点被访问
flag[i] = true;
//将该节点打印
System.out.print(num[i] + " ");
//寻找与num[i]节点相连的下一个访问节点
for (int j = 0; j < number; j++) {
//从标志数组第0位开始顺序查找,如果这一点未被访问,且与第num[i]个节点相连
if (flag[j] == false && edges[i][j] == 1) {
//递归
DFS(j);
}
}
}
void DFS_Map(){
flag = new boolean[number];
Stack<Integer> stack =new Stack<Integer>();
for(int i=0;i<number;i++){
if(flag[i]==false){
flag[i]=true;
System.out.print(num[i]+" ");
stack.push(i);
}
while(!stack.isEmpty()){
int k = stack.pop();
for(int j=0;j<number;j++){
if(edges[k][j]==1&&flag[j]==false){
flag[j]=true;
System.out.print(num[j]+" ");
stack.push(j);
break;
}
}
}
}
}
//测试类
public static void main(String[] args) {
Graph graph = new Graph();
System.out.println("DFS递归:");
graph.DFSTraverse();
System.out.println();
System.out.println("DFS非递归:");
graph.DFS_Map();
}
}
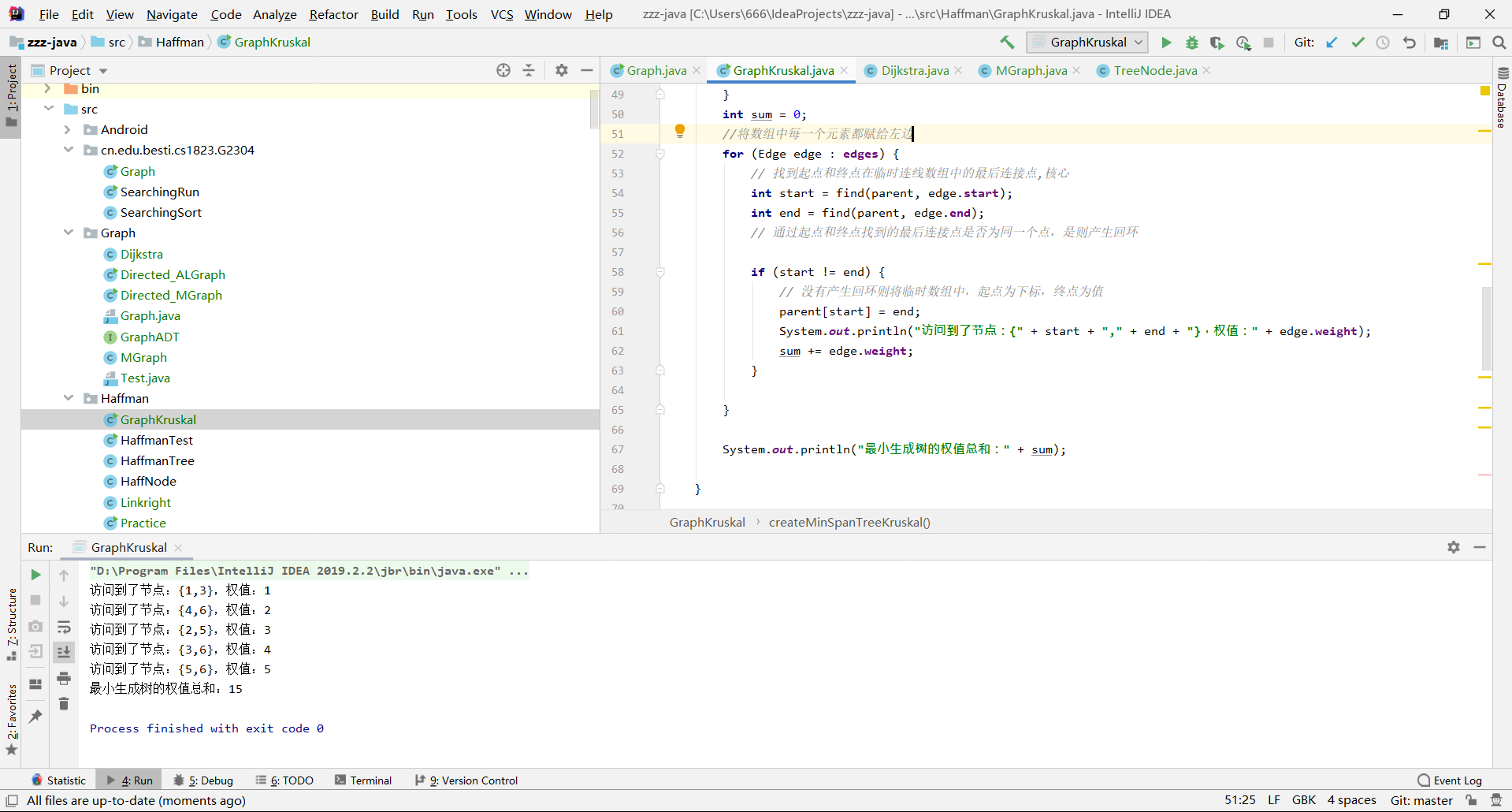
- 问题2: kruskal(克鲁斯卡尔)算法的实现思路是什么,应该如何具体实现
- 问题2解决方案:
- 现将所有边进行权值的从小到大排序
- 定义一个一维数组代表连接过的边,数组的下标为边的起点,值为边的终点
- 按照排好序的集合用边对顶点进行依次连接,连接的边则存放到一维数组中
- 用一维数组判断是否对已经连接的边能构成回路,有回路则无效,没回路则是一条有效边
- 重复3,4直至遍历完所有的边为止,即找到最小生成树
public class GraphKruskal {
//定义Edge型数组
private Edge[] edges;
private int edgeSize;
public GraphKruskal(int edgeSize) {
//参数个数
this.edgeSize = edgeSize;
edges = new Edge[edgeSize];
createEdgeKruskal();
}
//创建边的集合,从小到大
private void createEdgeKruskal() {
Edge edge0 = new Edge(1, 3, 1);
Edge edge1 = new Edge(4, 6, 2);
Edge edge2 = new Edge(2, 5, 3);
Edge edge3 = new Edge(3, 6, 4);
Edge edge4 = new Edge(2, 3, 5);
Edge edge5 = new Edge(3, 4, 5);
Edge edge6 = new Edge(1, 4, 5);
Edge edge7 = new Edge(3, 5, 6);
Edge edge8 = new Edge(1, 2, 6);
Edge edge9 = new Edge(5, 6, 6);
edges[0] = edge0;
edges[1] = edge1;
edges[2] = edge2;
edges[3] = edge3;
edges[4] = edge4;
edges[5] = edge5;
edges[6] = edge6;
edges[7] = edge7;
edges[8] = edge8;
edges[9] = edge9;
}
//kruskal算法创建最小生成树
public void createMinSpanTreeKruskal() {
// 定义一个一维数组,下标为连线的起点,值为连线的终点
int[] parent = new int[edgeSize];
for (int i = 0; i < edgeSize; i++) {
parent[i] = 0;
}
int sum = 0;
//将数组中每一个元素都赋给左边
for (Edge edge : edges) {
// 找到起点和终点在临时连线数组中的最后连接点,核心
int start = find(parent, edge.start);
int end = find(parent, edge.end);
// 通过起点和终点找到的最后连接点是否为同一个点,是则产生回环
if (start != end) {
// 没有产生回环则将临时数组中,起点为下标,终点为值
parent[start] = end;
System.out.println("访问到了节点:{" + start + "," + end + "},权值:" + edge.weight);
sum += edge.weight;
}
}
System.out.println("最小生成树的权值总和:" + sum);
}
// 获取集合的最后节点
private int find(int parent[], int index) {
while (parent[index] > 0) {
index = parent[index];
}
return index;
}
//连接顶点的边
class Edge {
private int start;
private int end;
private int weight;
public Edge(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
}
public static void main(String[] args) {
GraphKruskal graphKruskal = new GraphKruskal(10);
graphKruskal.createMinSpanTreeKruskal();
}
}
- 问题3:Dijkstra的作用是什么,如何具体实现Dijkstra算法
- 问题3解决方案:迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
- 具体实现思路详见代码
public class Dijkstra {
public static final int M = 10000; // 代表正无穷
public static void main(String[] args) {
// 二维数组每一行分别是 A、B、C、D、E 各点到其余点的距离,
// A -> A 距离为0, 常量M 为正无穷
int[][] weight1 = {
{0, 13, 8, M, 30, M, 32},
{M, 0, M, M, M, 9, 7 },
{M, M, 0, 5, M, M , M},
{M, M, M, 0, 6, M , M},
{M, M, M, M, 0, 2 , M},
{M, M, M, M, M, 0 ,17},
{M, M, M, M, M, M , 0},
};
int start = 0;
int[] shortPath = dijkstra(weight1, start);
for (int i = 0; i < shortPath.length; i++)
System.out.println("从" + start + "出发到" + i + "的最短距离为:" + shortPath[i]);
}
public static int[] dijkstra(int[][] weight, int start) {
// 接受一个有向图的权重矩阵,和一个起点编号start(从0编号,顶点存在数组中)
// 返回一个int[] 数组,表示从start到它的最短路径长度
int n = weight.length; // 顶点个数
int[] shortPath = new int[n]; // 保存start到其他各点的最短路径
String[] path = new String[n]; // 保存start到其他各点最短路径的字符串表示
for (int i = 0; i < n; i++)
path[i] = new String(start + "-->" + i);
int[] visited = new int[n]; // 标记当前该顶点的最短路径是否已经求出,1表示已求出
// 初始化,第一个顶点已经求出
shortPath[start] = 0;
visited[start] = 1;
for (int count = 1; count < n; count++) { // 要加入n-1个顶点
int k = -1; // 选出一个距离初始顶点start最近的未标记顶点
int dmin = Integer.MAX_VALUE;
for (int i = 0; i < n; i++) {
if (visited[i] == 0 && weight[start][i] < dmin) {
dmin = weight[start][i];
k = i;
}
}
// 将新选出的顶点标记为已求出最短路径,且到start的最短路径就是dmin
shortPath[k] = dmin;
visited[k] = 1;
// 以k为中间点,修正从start到未访问各点的距离
for (int i = 0; i < n; i++) {
//如果 '起始点到当前点距离' + '当前点到某点距离' < '起始点到某点距离', 则更新
if (visited[i] == 0 && weight[start][k] + weight[k][i] < weight[start][i]) {
weight[start][i] = weight[start][k] + weight[k][i];
path[i] = path[k] + "-->" + i;
}
}
}
for (int i = 0; i < n; i++) {
System.out.println("从" + start + "出发到" + i + "的最短路径为:" + path[i]);
}
System.out.println("=====================================");
return shortPath;
}
}

代码托管
(
)
上周考试错题总结
- 无
结对及互评
评分标准
-
正确使用Markdown语法(加1分):
- 不使用Markdown不加分
- 有语法错误的不加分(链接打不开,表格不对,列表不正确...)
- 排版混乱的不加分
-
模板中的要素齐全(加1分)
- 缺少“教材学习中的问题和解决过程”的不加分
- 缺少“代码调试中的问题和解决过程”的不加分
- 代码托管不能打开的不加分
- 缺少“结对及互评”的不能打开的不加分
- 缺少“上周考试错题总结”的不能加分
- 缺少“进度条”的不能加分
- 缺少“参考资料”的不能加分
-
教材学习中的问题和解决过程, 一个问题加1分
-
代码调试中的问题和解决过程, 一个问题加1分
-
本周有效代码超过300分行的(加2分)
- 一周提交次数少于20次的不加分
-
其他加分:
- 周五前发博客的加1分
- 感想,体会不假大空的加1分
- 排版精美的加一分
- 进度条中记录学习时间与改进情况的加1分
- 有动手写新代码的加1分
- 课后选择题有验证的加1分
- 代码Commit Message规范的加1分
- 错题学习深入的加1分
- 点评认真,能指出博客和代码中的问题的加1分
- 结对学习情况真实可信的加1分
-
扣分:
- 有抄袭的扣至0分
- 代码作弊的扣至0分
- 迟交作业的扣至0分
点评模板:
-
博客中值得学习的或问题:
- 讲解内容较为丰富
-
代码中值得学习的或问题:
- 结合所学,给出了算法的具体实现
-
基于评分标准,我给本博客打分:18分
点评过的同学博客和代码
其他(感悟、思考等,可选)
- 数据结构学习也算到尾声了,图这一章算法比较丰富,需要我们花费时间逐一认真理解,并落实到代码实现。只有这样,我们对数据结构的理解才能真正融会贯通
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 200/200 | 2/2 | 20/20 | |
| 第二周 | 300/500 | 2/4 | 18/38 | |
| 第三周 | 500/1000 | 3/7 | 22/60 | |
| 第四周 | 300/1300 | 2/9 | 30/90 | |
| 第五周 | 1600/2900 | 2/11 | 20/110 | |
| 第六周 | 981 /3881 | 2/12 | 25/135 | |
| 第七周 | 1700/5518 | 3/15 | 45/180 | |
| 第八周 | 700/6200 | 2/17 | 20/200 | |
| 第九周 | 4300/10500 | 2/19 | 30/230 | |
| 第十周 | 2064/12564 | 1/20 | 30/260 |
尝试一下记录「计划学习时间」和「实际学习时间」,到期末看看能不能改进自己的计划能力。这个工作学习中很重要,也很有用。
耗时估计的公式:Y=X+X/N ,Y=X-X/N,训练次数多了,X、Y就接近了。
-
计划学习时间:30小时
-
实际学习时间:30小时
-
改进情况:
(有空多看看现代软件工程 课件
软件工程师能力自我评价表)




