《数据结构与面向对象程序设计》第九周学习总结
学号 2019-2020-1 《数据结构与面向对象程序设计》第九周学习总结
教材学习内容总结
-
非线性数据结构——————树,元素组织为层次结构
-
树的基本概念
- 概念:树由一组结点和一组边构成,通过结点来存储元素,边表示节点之间的连接
-
树的相关术语:
- 根节点:树中唯一没有父节点的节点,位于树的顶层
- 内部结点:一颗树中既不是根结点也不是叶结点的称为内部结点
- 叶子:没有孩子的结点称之为叶子
- 高度/深度:一颗树的层数
- 度/阶:一棵树中任一结点所具有的最大孩子数目
-
树的分类
- 分类标准:任一结点可以具有的最大孩子数目,称为度。我们主要学习二叉树,即每个结点下最多有两个孩子的树。
- 完全树:底层叶子都位于树的左边的平衡树称为完全树
- 满树:在一颗n元树中,所有叶子都位于一层,且除叶子外的每个结点都有n个孩子,则该树被称作满树
- 平衡:树的所有叶子之间相差层数不超过一层的树称为稳定的树
-
二叉树
-
性质
- 二叉树的每一个结点最多具有两个孩子结点
- 在二叉树的第i层最多有2i-1个结点
- 深度为k的二叉树最多有2k-1个结点
- 对任何一棵二叉树,如果其叶结点个数为n0,度为2的结点数为n2则有n0=n2+1
-
完全二叉树
- 对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树
-
满二叉树
- 每层结点都是满的二叉树
-
树的遍历(四种方法)
-
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有的结点,使得每个结点被访问依次且仅被访问一次
- 前序遍历:若树为空,则空操作返回。否则,先访问根节点,然后前序遍历左子树,再前序遍历右子树
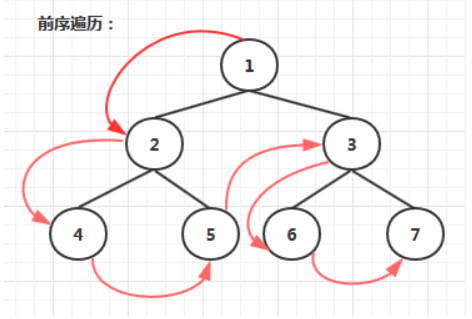
- 代码实现
- 前序遍历:若树为空,则空操作返回。否则,先访问根节点,然后前序遍历左子树,再前序遍历右子树
public static void preOrderTraverse(Node root) {
Stack<Node> stack = new Stack<>();
Node node1 = root;
while (node1 != null || !stack.empty()) {
if (node1 != null) {
System.out.print(node1.val + " ");
stack.push(node1);
node1 = node1.left;
} else {
Node tem = stack.pop();
node1 = tem.right;
}
}
}
- 中序遍历:若树为空,则空操作返回。否则,从根节点开始(注意并不是先访问根节点),中序遍历根节点的左子树,然后是访问根节点,最后中序遍历根节点的右子树
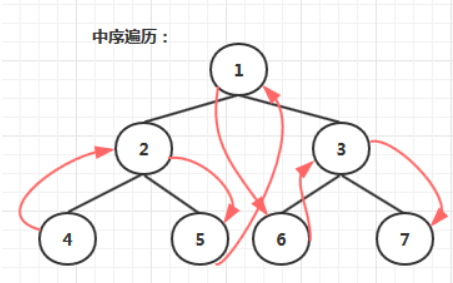
public static void inOrderTraverse(Node root) {
Stack<Node> stack = new Stack<>();
Node node1 = root;
while (node1 != null || !stack.isEmpty()) {
if (node1 != null) {
stack.push(node1);
node1 = node1.left;
} else {
Node tem = stack.pop();
System.out.print(tem.val + " ");
node1 = tem.right;
}
}
}
- 后续遍历:若树为空,则空操作返回。否则,从左到右先叶子后节点的方式遍历访问左右子树,最后访问根节点

public static void postOrder(Node root) {
if (root != null) {
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val + " ");
}
}
- 层序遍历:若树为空,则空操作返回。否则,从树的第一层,也就是根节点开始访问,从上到下逐层遍历,在同一层中,按从左到右的顺序结点逐个访问

public static void levOrder(Node root) {
if (root != null) {
Node p = root;
Queue<Node> queue = new LinkedList<>();
queue.add(p);
while (!queue.isEmpty()) {
p = queue.poll();
System.out.print(p.val + " ");
if (p.left != null) {
queue.add(p.left);
}
if (p.right != null) {
queue.add(p.right);
}
}
}
}
- 二叉查找树
- 概念:一棵具有下列性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 左、右子树也分别为二叉查找树
- 没有元素相等的点
- 也可以这么说:左孩子小于父结点,而父结点又小于或等于右孩子
操作: - addElement:向树中添加一个元素
- removeElement:从树中删除一个元素
- removeAllOccurrences:从树中删除所指定元素的任何存在
- removeMin:删除树中的最小元素
- removeMax:删除树中的最大元素
- findMin:返回树中的最小元素的引用
- findMax:返回树中的最大元素引用
- 递归算法(调用自己):实现二叉查找树算法比较方便
- 非递归
- 最优二叉树/哈夫曼树:平均带权长度最短的二叉树
- 权值越大的编码离根越近
- 取两个最小的,相加等于一个值,再重复排序插入
教材学习中的问题和解决过程
-
问题1:平衡二叉查找树有什么作用以及如何实现?
-
问题1解决方案:平衡二叉树的概念:一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。如果普通的二叉查找树在不断插入后失去平衡,最终可能会变成链表的形式,使查找效率大大降低。(如右图)所以我们需要二叉树保持平衡
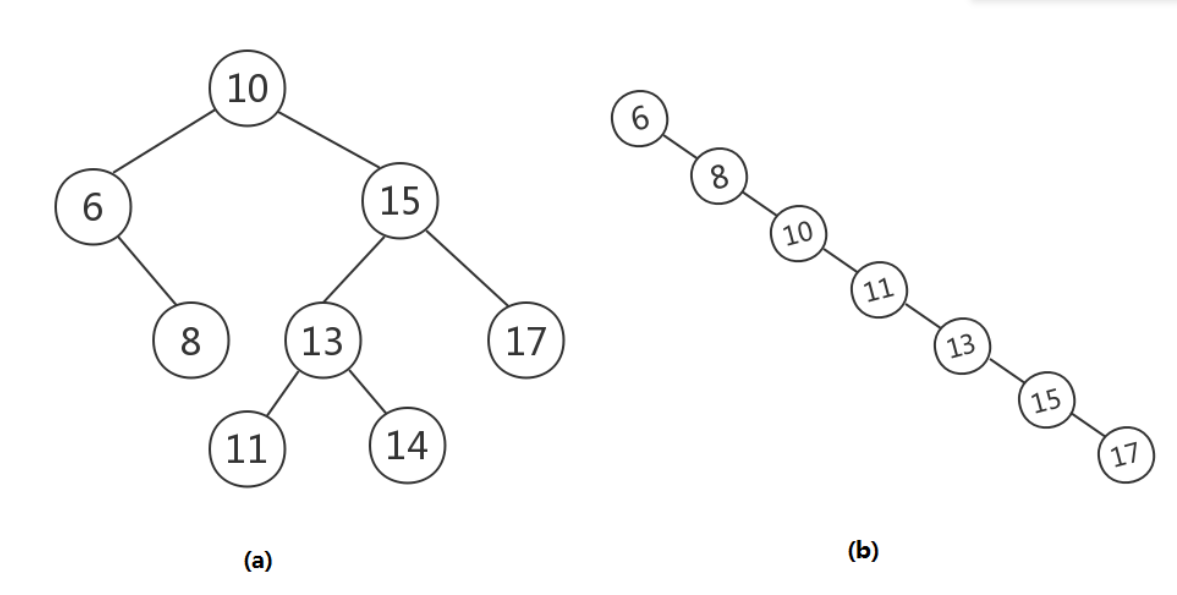
-
非平衡二叉查找树改变成为平衡二叉查找树主要有四种方法:右旋,左旋,左右旋,右左旋
- 右旋,通常是指左孩子绕着其父结点向右旋转,一般适用于左子树长于右子树的情况
- 左旋,通常是指右孩子绕着其父结点向左旋转,一般适用于右子树长于左子树的情况
- 王老师上课讲到,可以把二叉树平衡理解为转动一条项链上的珠子。具体来说,就是左旋就是往左变换,右旋就是往右变换。不管是左旋还是右旋,旋转的目的都是将节点多的一支出让节点给另一个节点少的一支。
- 这个还要根据具体实例进行细化研究,再深一步可能还要用到复杂的红黑树
-
问题2:二叉查找树删除方法的实现比较复杂,如何考虑多种情况删除?
-
问题2解决方案:分三种情况进行讨论
- 如果删除的是叶节点,可以直接删除
- 如果被删除的元素有一个子节点,可以将子节点直接移到被删除元素的位置,即应该调整要被删除的父结点(指向被删除结点的孩子结点
- 如果有两个子节点,这时候就采用中序遍历,找到待删除的节点的后继节点,将其与待删除的节点互换,此时待删除节点的位置已经是叶子节点,可以直接删除 。即用被删除节点的右子树的最小的数据替代要被删除结点的数据,并递归删除用于替换的结点(此时该结点已为空)
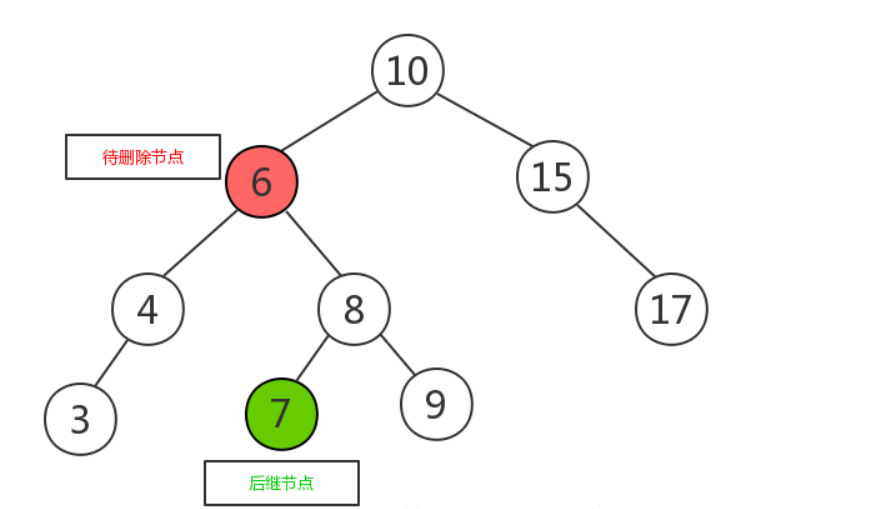
- 将待删除节点与后继节点互换,变成如下图所示:
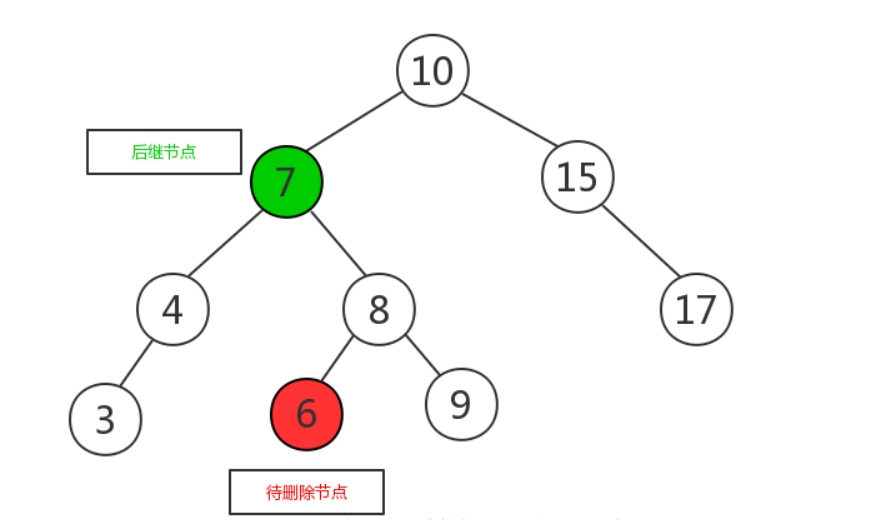
- 将待删除元素删除
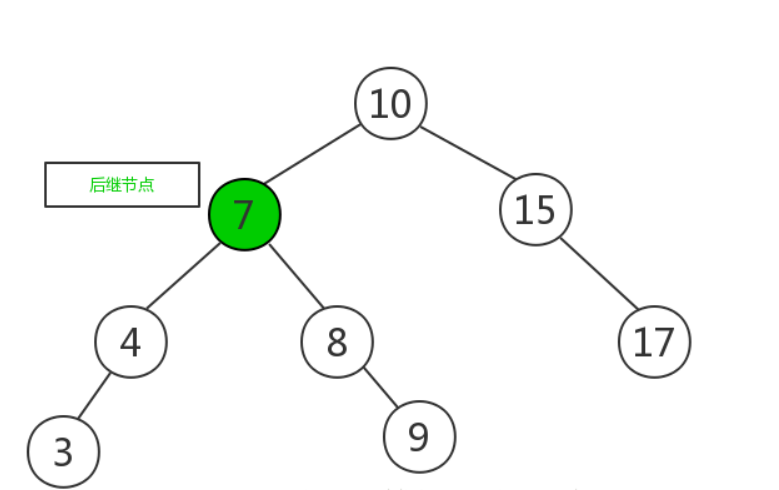
-
问题3:递归和迭代的区别在哪里?递归的优势是什么?
-
问题3解决方案:递归,其实就是函数自己调用自己。迭代是指利用变量的原值推算出变量的一个新值,可以理解为A不停的调用B。迭代使用的是循环(for,while,do-while)或者迭代器,当循环条件不满足时退出。而递归一般是函数递归,可以是自身调用自身,只需有一个结束递归的条件。递归的优势是简洁明了,缺点是浪费大量的空间,效率较低
代码调试中的问题和解决过程
-
问题1:在使用树处理中缀表达式转换为后缀表达式中输出出现了问题,
toString方法无法正常使用

-
问题1解决方案:经检查
toString方法,我的结点部分使用的是整型部分使用的是泛型,不适应于字符串型。也无法进行正常的比较,最终只能再次重写整个方法 -
问题2:在编写作业17.1时,遍历时迭代器出现了问题
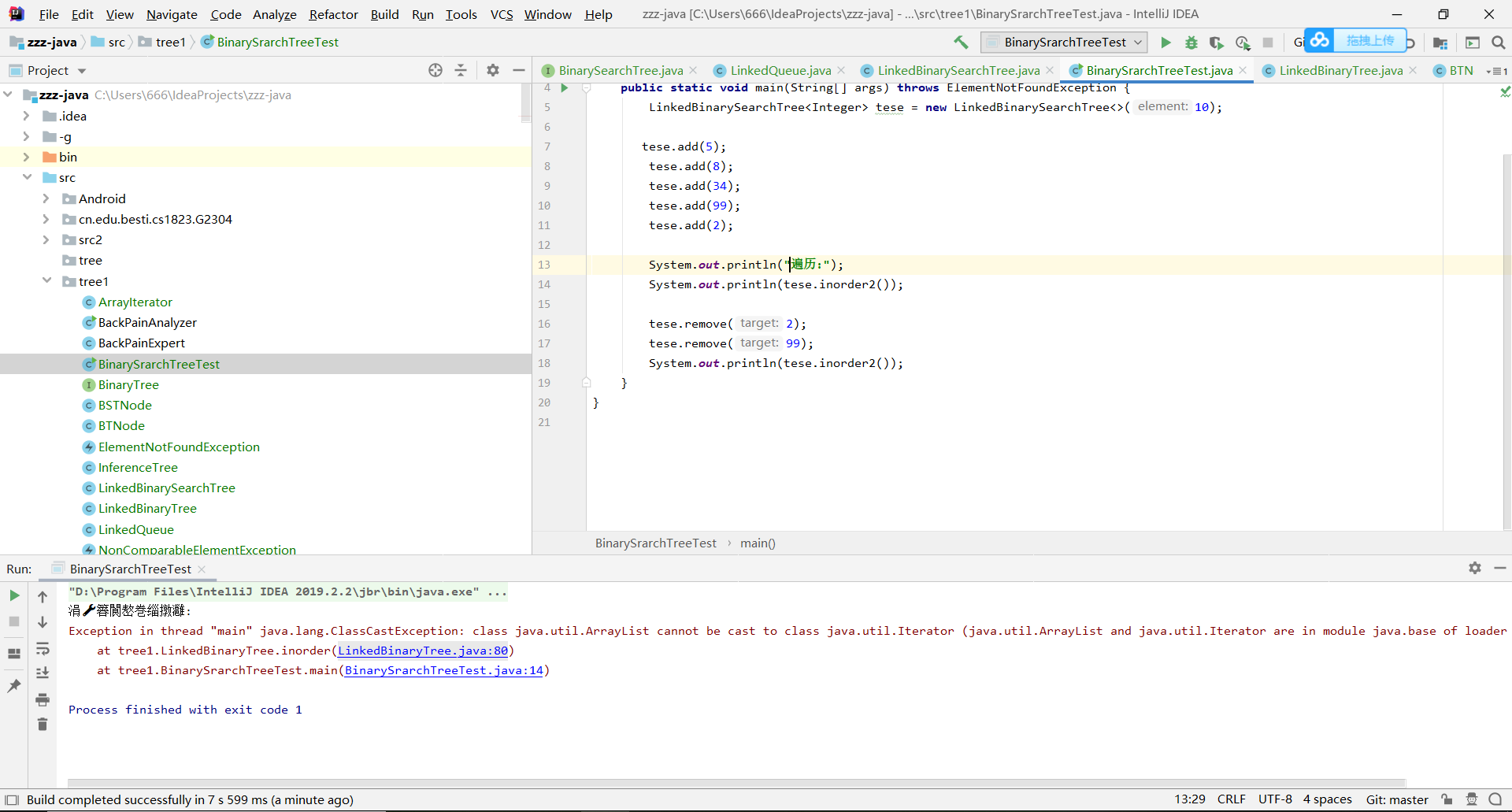
-
问题2解决方案:检查迭代器的代码,发现我照抄了书上的Iterator
类,将其修改为ArrayList 类即可正常运行
public ArrayList<T> inorder() {
ArrayList<T> iter = new ArrayList<T>();
if (root != null)
root.inorder(iter);
return iter;
}
代码托管
(
)
上周考试错题总结
- Which of the following is not a valid postfix expression?
- 4 + 5
- 看错了,是not
- When one type of object contains a link to another object of the same type, the object is sometimes called __________ .
- A self-referential object is one that refers to another object of the same type.
- 自引用居然可以指向同一类型的不同目标,之前确实不理解
- The import keyword is used to define your own packages.
- The package keyword is used to define packages of source code in Java.
- 理解错误,import是用来导入包中的源代码
- In a linked implementation of a stack, a pushed element should be added to the end of the list.
- push操作应该放在最前面,否则无法实现栈的后进先出(前面的有点学混了,要及时复习)
结对及互评
评分标准
-
正确使用Markdown语法(加1分):
- 不使用Markdown不加分
- 有语法错误的不加分(链接打不开,表格不对,列表不正确...)
- 排版混乱的不加分
-
模板中的要素齐全(加1分)
- 缺少“教材学习中的问题和解决过程”的不加分
- 缺少“代码调试中的问题和解决过程”的不加分
- 代码托管不能打开的不加分
- 缺少“结对及互评”的不能打开的不加分
- 缺少“上周考试错题总结”的不能加分
- 缺少“进度条”的不能加分
- 缺少“参考资料”的不能加分
-
教材学习中的问题和解决过程, 一个问题加1分
-
代码调试中的问题和解决过程, 一个问题加1分
-
本周有效代码超过300分行的(加2分)
- 一周提交次数少于20次的不加分
-
其他加分:
- 周五前发博客的加1分
- 感想,体会不假大空的加1分
- 排版精美的加一分
- 进度条中记录学习时间与改进情况的加1分
- 有动手写新代码的加1分
- 课后选择题有验证的加1分
- 代码Commit Message规范的加1分
- 错题学习深入的加1分
- 点评认真,能指出博客和代码中的问题的加1分
- 结对学习情况真实可信的加1分
-
扣分:
- 有抄袭的扣至0分
- 代码作弊的扣至0分
- 迟交作业的扣至0分
点评模板:
-
博客中值得学习的或问题:
- 问题探究不够深入
-
代码中值得学习的或问题:
- 代码commit不标准,缺少注释不宜看懂
-
基于评分标准,我给本博客打分:16X分。得分情况如下:xxx
点评过的同学博客和代码
其他(感悟、思考等,可选)
- 太难了,这堆算法环环相扣,思路也不大好理解。书上的方法补写起来不容易,也不给一点提示。编程时知道大体的思路和具体实现是两回事,苦于找不到正确的编程方法
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 200/200 | 2/2 | 20/20 | |
| 第二周 | 300/500 | 2/4 | 18/38 | |
| 第三周 | 500/1000 | 3/7 | 22/60 | |
| 第四周 | 300/1300 | 2/9 | 30/90 | |
| 第五周 | 1600/2900 | 2/11 | 20/110 | |
| 第六周 | 981 /3881 | 2/12 | 25/135 | |
| 第七周 | 1700/5518 | 3/15 | 45/180 | |
| 第八周 | 700/6200 | 2/17 | 20/200 | |
| 第九周 | 4300/10500 | 3/20 | 30/230 |
尝试一下记录「计划学习时间」和「实际学习时间」,到期末看看能不能改进自己的计划能力。这个工作学习中很重要,也很有用。
耗时估计的公式:Y=X+X/N ,Y=X-X/N,训练次数多了,X、Y就接近了。
-
计划学习时间:30小时
-
实际学习时间:30小时
-
改进情况:
(有空多看看现代软件工程 课件
软件工程师能力自我评价表)





