题解【luogu4168 [Violet]蒲公英】

Description

给出一个长度为 \(n\) 序列 \(a\) ，\(m\) 次询问，每次询问区间 \([l,r]\) 里的众数（出现次数最多的数）。若有多个，输出最小的。

\(a_i \leq 10^9, n \leq 40000, m \leq 50000\)，强制在线。

Solution

\(a_i \leq 10^9\) ，先离散化。然后

算法一：暴力 \(n ^ 2\) ，预计得分 20 ； 实际得分 20 （开了 O2 直接变成 85 啥操作）

算法二：\(n \leq 40000\) ， 看来需要搬出分块大法。

预处理出两个数组：

\(p[i][j]\)：表示第 \(i\) 个块 到第 \(j\) 个块的（最小的）众数。

\(s[i][j]\)：类似于前缀和，在前 \(i\) 个（包括 \(i\) ）个块中 \(j\) （离散化之后的值）出现了几次。

如何预处理 \(p,s\)

对于 \(s\) ，直接每个块扫一遍，复杂度 \(O(n \sqrt n)\)

对于 \(p\) ，双重循环枚举 \(i,j\)，开一个数组暴力统计每个数出现了多少次。复杂度 \(O(\sqrt n \sqrt n \sqrt n)=O(n \sqrt n)\)

预处理 \(p,s\) 有啥用呢？对于一个询问 \([l,r]\) ，设 \(l\) 在第 \(posl\) 个块中，\(r\) 在第 \(posr\) 个块中。那么分两种情况：

第一种：\(posr - posl <= 1\)，直接暴力扫 \(l,r\)，复杂度 \(O(\sqrt n)\)

第二种：\(posr - posl >= 2\)，如下图：

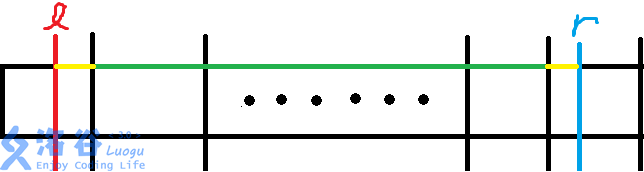
红线就是 \(l\)，蓝线就是 \(r\)，黑线是块与块的分割线。

答案 \(\in\) \(\{\text{黄线中的元素}\} \cup \{\text{绿线的众数}\}\)

绿线的众数在之前已经预处理好了，对于黄线中的每一个元素在区间\([l,r]\)中出现的次数就是 在黄线中出现的次数 + 在绿线中出现的次数。

对于在黄线中出现的次数，可以直接扫，复杂度 \(O(\sqrt n)\)

对于在绿线中出现的次数，可以根据之前处理的前缀和算出。

这样每个元素就可以在 \(O(\sqrt n)\) 的时间内求出出现次数，然后就可以愉快的AC神仙分块黑题了了。 （细节很多，调了很久）

Code

#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 40040;
const int K = 220;
int n, m, L, len, sum[K][N], vis[N];
int tmpnum[N], B[N], last, pre[N];
struct getin {
    int id, d, se;
}a[N];
struct node {
    int num, s;
}p[K][K];
inline bool cmp1(getin x, getin y) { return x.d < y.d; }
inline bool cmp2(getin x, getin y) { return x.id < y.id; }
inline int getB(int x) {
    int ret = x / L;
    if(x % L) ret++;
    return ret;
}
inline void prework() {
    for(int i = 1; i <= len; i++) {
        memset(B, 0, sizeof(B)); node tmp;
        tmp.num = tmp.s = 0;
        for(int j = i; j <= len; j++) {
            for(int k = (j - 1) * L + 1; k <= min(n, j * L); k++) {
                B[a[k].se]++;
                if(B[a[k].se] > tmp.s) {
                    tmp.num = a[k].se;
                    tmp.s = B[a[k].se];
                }
                else if(B[a[k].se] == tmp.s)
                    tmp.num = min(tmp.num, a[k].se), 
                    tmp.s = B[a[k].se];
            }
            p[i][j] = tmp;
        }
    }
    for(int i = 1; i <= len; i++) {
        for(int j = 1; j <= n; j++) sum[i][a[j].se] = sum[i - 1][a[j].se];
        for(int j = (i - 1) * L + 1; j <= min(n, i * L); j++) 
            sum[i][a[j].se]++;
    }
}
int main() {
    scanf("%d%d", &n, &m); L = sqrt(n);
    len = (n + L - 1) / L;
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i].d), a[i].id = i;
    sort(a + 1, a + n + 1, cmp1); a[0].d = -1;
    for(int i = 1; i <= n; i++) {
        a[i].se = a[i - 1].se;
        if(a[i - 1].d != a[i].d) 
            a[i].se++;
        pre[a[i].se] = a[i].d;
    }
    sort(a + 1, a + n + 1, cmp2);
    prework(); 
    for(int i = 1; i <= m; i++) {
        int l, r; scanf("%d%d", &l, &r);
        l = (l + last - 1) % n + 1;
        r = (r + last - 1) % n + 1;
        if(l > r) swap(l, r);
        int posl = getB(l), posr = getB(r);
         if(posr - posl <= 2) {
            int ans = 0;
            for(int j = l; j <= r; j++) tmpnum[a[j].se] = 0;
            for(int j = l; j <= r; j++) {
                tmpnum[a[j].se]++;
                if(tmpnum[a[j].se] > tmpnum[ans]) ans = a[j].se;
                else if(tmpnum[a[j].se] == tmpnum[ans]) ans = min(ans, a[j].se);
            }
            printf("%d\n", last = pre[ans]);
        } 
        else {
            int ans = p[posl + 1][posr - 1].num;
            tmpnum[ans] = 0, vis[ans] = 0;
            for(int j = l; j <= min(n, posl * L); j++) tmpnum[a[j].se] = 0, vis[a[j].se] = 0;
            for(int j = (posr - 1) * L + 1; j <= r; j++) tmpnum[a[j].se] = 0, vis[a[j].se] = 0;
            for(int j = l; j <= min(n, posl * L); j++) tmpnum[a[j].se]++;
            for(int j = (posr - 1) * L + 1; j <= r; j++) tmpnum[a[j].se]++;
            int MXnum, MX = 0;
            for(int j = l; j <= min(n, posl * L); j++)
                if(!vis[a[j].se]) {
                    vis[a[j].se] = 1;
                    int val = tmpnum[a[j].se] + sum[posr - 1][a[j].se] - sum[posl][a[j].se];
                    if(MX < val)
                        MX = val, 
                        MXnum = a[j].se;
                    else if(MX == val) MXnum = min(MXnum, a[j].se);
                }
            for(int j = (posr - 1) * L + 1; j <= r; j++)
                if(!vis[a[j].se]) {
                    vis[a[j].se] = 1;
                    int val = tmpnum[a[j].se] + sum[posr - 1][a[j].se] - sum[posl][a[j].se];
                    if(MX < val)
                        MX = val, 
                        MXnum = a[j].se;
                    else if(MX == val) MXnum = min(MXnum, a[j].se);
                }
            if(MX > tmpnum[ans] + p[posl + 1][posr - 1].s) ans = MXnum;
            else if(MX == tmpnum[ans] + p[posl + 1][posr - 1].s) ans = min(ans, MXnum);
            printf("%d\n", last = pre[ans]);
        } 
    }
    return 0;
}