数学题乱做
AT3728 [ARC087D] Squirrel Migration
首先要保证值最大,再去求排列数
考虑什么情况下值是最大的,对于一条边 \((u,v)\),将它割掉后会形成的两个联通快 \(S,T\),那么这条边产生的贡献最大是 \(2\times min(|S|,|T|)\)
如何让贡献最大呢,不难发现找到重心即可,这样重心连出去的边贡献都可以达到最大,只需要求出重心的每个子树内的点对应的点都在子树外的方案数,因为这样可以保证重心连出去的边被经过最多次,并且每棵子树内的边也被经过最多次。
使用容斥计算答案
设 \(f_i\) 表示钦定 \(i\) 个点不合法的方案数,那么 \(Ans=\sum (-1)^i(n-i)!f_i\)
对于一个大小为 \(x\) 的子树,容易得到该子树的 \(f_i=\binom x i x^{\underline i}\),然后在重心处背包合并一下即可
Code
#include <bits/stdc++.h>
#define ll long long
#define db double
#define gc getchar
#define pc putchar
#define pb push_back
using namespace std;
namespace IO
{
template <typename T>
void read(T &x)
{
x = 0; bool f = 0; char c = gc();
while(!isdigit(c)) f |= c == '-', c = gc();
while(isdigit(c)) x = x * 10 + c - '0', c = gc();
if(f) x = -x;
}
template <typename T, typename ...Args>
void read(T &x, Args &...args) {read(x), read(args...);}
template <typename T>
void write(T x)
{
if(x < 0) pc('-'), x = -x;
if(x > 9) write(x / 10);
pc('0' + x % 10);
}
}
using namespace IO;
const int N = 5005;
const int mod = 1e9 + 7;
int n;
vector <int> G[N];
int rt, all, siz[N], maxp[N];
void getroot(int u, int fa)
{
siz[u] = 1, maxp[u] = 0;
for(auto v : G[u])
{
if(v == fa) continue;
getroot(v, u);
siz[u] += siz[v];
maxp[u] = max(maxp[u], siz[v]);
}
maxp[u] = max(maxp[u], all - siz[u]);
if(!rt || maxp[u] < maxp[rt]) rt = u;
return;
}
int add(int x) {return x < mod ? x : x - mod;}
int qpow(int a, int b)
{
int res = 1;
while(b)
{
if(b & 1) res = 1ll * res * a % mod;
a = 1ll * a * a % mod, b >>= 1;
}
return res;
}
int fac[N], ifac[N], f[N];
int C(int n, int m)
{
return n < m ? 0 : 1ll * fac[n] * ifac[m] % mod * ifac[n - m] % mod;
}
void init(int n)
{
fac[0] = 1;
for(int i = 1; i <= n; i++) fac[i] = 1ll * fac[i - 1] * i % mod;
ifac[n] = qpow(fac[n], mod - 2);
for(int i = n - 1; i >= 0; i--) ifac[i] = 1ll * ifac[i + 1] * (i + 1) % mod;
}
int main()
{
read(n); init(n);
for(int i = 1, u, v; i < n; i++)
read(u, v), G[u].pb(v), G[v].pb(u);
all = n;
getroot(1, 0);
getroot(rt, 0);
f[0] = 1;
for(auto v : G[rt])
{
int x = siz[v];
for(int i = n; i >= 0; i--)
for(int j = 1; j <= min(i, x); j++)
f[i] = add(f[i] + 1ll * f[i - j] * C(x, j) % mod * fac[x] % mod * ifac[x - j] % mod);
}
int ans = 0;
for(int i = 0; i <= n; i++)
ans = add(ans + (i & 1 ? mod - 1ll : 1ll) * f[i] % mod * fac[n - i] % mod);
write(ans), pc('\n');
return 0;
}
// A.S.
AT2384 [AGC015F] Kenus the Ancient Greek
本题需要天启(雾
先看第一问,我们反着模拟更相减损术向上走,发现就是斐波那契数列,因此只需要找到最大的 \(f_i\le n,f_{i+1}\le m\) 的 \(i\) 即可,记答案为 \(mx\)。
现在我们需要求出 \(cnt(i,j)=mx\) 的二元组个数,将这种二元组称为 \(good\ pair\),个数极多,无法直接算,但是我们发现,很多 \(good\ pair\) 在进行一次辗转相除后会变成一样的,我们把这种一样的 \(good\ pair\) 称为 \(excelent\ pair\),所以只需要找到所有 \(excelent\ pair\) 就能算出 \(good\ pair\) 的个数了。
对于一个 \(excelent\ pair\ (a,b)\),它能表示的 \(good\ pair\) 为 \((a,b+ka),(b,b+ka)\),在 \((n,m)\) 的范围内 \(k\) 是可以直接计算的。
因此只需要预处理出所有斐波那契数列构成的 \(excelent\ pair\)。
Code
#include <bits/stdc++.h>
#define int long long
#define db double
#define gc getchar
#define pc putchar
#define pb push_back
#define fi first
#define se second
#define INF 1e18
using namespace std;
namespace IO
{
template <typename T>
void read(T &x)
{
x = 0; bool f = 0; char c = gc();
while(!isdigit(c)) f |= c == '-', c = gc();
while(isdigit(c)) x = x * 10 + c - '0', c = gc();
if(f) x = -x;
}
template <typename T, typename ...Args>
void read(T &x, Args &...args) {read(x), read(args...);}
template <typename T>
void write(T x)
{
if(x < 0) pc('-'), x = -x;
if(x > 9) write(x / 10);
pc('0' + x % 10);
}
}
using namespace IO;
typedef pair<int, int> P;
const int N = 100;
const int mod = 1e9 + 7;
int n, f[N];
vector <P> g[N];
signed main()
{
f[0] = f[1] = 1;
for(n = 1; f[n] + f[n - 1] <= INF; )
n++, f[n] = f[n - 1] + f[n - 2];
g[1].pb(P(1, 2));
for(int i = 2; i <= n; i++)
{
for(auto j : g[i - 1])
g[i].pb(P(j.se, j.fi + j.se));
g[i].pb(P(f[i + 1], f[i - 1] + f[i + 1]));
}
int T; read(T);
while(T--)
{
int x, y; read(x, y);
if(x > y) swap(x, y);
int mx = 1, ans = 0;
while(mx + 2 <= n && f[mx + 1] <= x && f[mx + 2] <= y) mx++;
for(auto p : g[mx])
{
if(p.se <= x) (ans += (x - p.se) / p.fi + 1) %= mod;
if(p.fi <= x && p.se <= y) (ans += (y - p.se) / p.fi + 1) %= mod;
}
if(mx == 1) (ans += x) %= mod;
write(mx), pc(' '), write(ans), pc('\n');
}
return 0;
}
// A.S.
AT2062 [AGC005D] ~K Perm Counting
题意可以转化为:
在一个 \(n\times n\) 的棋盘上放 \(n\) 个车,每行每列只有一个,同时有两条对角线上不能放的方案数。
看图理解一下(来自 Dreamunk 的题解)
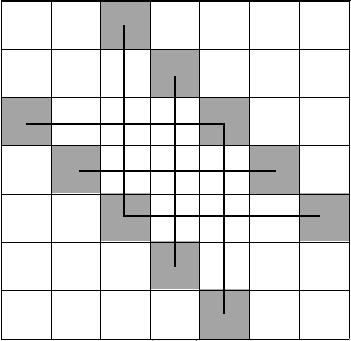
考虑容斥,设 \(f_i\) 表示钦定有 \(i\) 个车放在阴影中的方案数,那么 \(Ans=\sum (-1)^i(n-i)!f_i\)
在计算 \(f_i\) 时依然要保证不能放在同一行/列
把不能同时放的格子连起来,然后形成了若干条链,再把这些链连起来,就可以 dp 了,除了两条链的交界处,都不能选相邻的两个点,提前把交界处标记一下
其中共有两种长度的链,手玩一下就行了(
Code
#include <bits/stdc++.h>
#define ll long long
#define db double
#define gc getchar
#define pc putchar
#define pb push_back
using namespace std;
namespace IO
{
template <typename T>
void read(T &x)
{
x = 0; bool f = 0; char c = gc();
while(!isdigit(c)) f |= c == '-', c = gc();
while(isdigit(c)) x = x * 10 + c - '0', c = gc();
if(f) x = -x;
}
template <typename T, typename ...Args>
void read(T &x, Args &...args) {read(x), read(args...);}
template <typename T>
void write(T x)
{
if(x < 0) pc('-'), x = -x;
if(x > 9) write(x / 10);
pc('0' + x % 10);
}
}
using namespace IO;
const int N = 2e3 + 5;
const int mod = 924844033;
int n, k, len, a[N << 1];
int fac[N], f[N << 1][N];
int main()
{
read(n, k);
a[len = 0] = 1;
for(int i = 1; i <= (n - k) % k; i++)
a[len += (n - k) / k + 1] = 1, a[len += (n - k) / k + 1] = 1;
for(int i = 1; i <= k - (n - k) % k; i++)
a[len += (n - k) / k] = 1, a[len += (n - k) / k] = 1;
f[0][0] = 1;
for(int i = 1; i <= len; i++)
for(int j = 0; j <= n; j++)
{
f[i][j] = f[i - 1][j];
if(j) f[i][j] = (f[i][j] + f[i - 1 - (!a[i - 1])][j - 1]) % mod;
}
fac[0] = 1;
for(int i = 1; i <= n; i++) fac[i] = 1ll * fac[i - 1] * i % mod;
int ans = 0;
for(int i = 0; i <= n; i++)
ans = (ans + (i & 1 ? -1ll : 1ll) * f[len][i] * fac[n - i] % mod + mod) % mod;
write(ans), pc('\n');
return 0;
}
// A.S.
CF618G Combining Slimes
设 \(a_{i,j}\) 表示使用 \(i\) 个格子,最左边是 \(j\) 的概率,转移 \(a_{i,j} = a_{i-1,j-1}\times a_{i,j-1}\),就是需要出现两个 \(j - 1\) 去凑 \(j\)。
但是 \(n\) 巨大,不能全算出来,我们发现 \(a_{i,j}\) 会越来越小,当 \(j\ge 50\) 时,\(a_{i,j}\) 已经几乎为 \(0\) 了,所以只需处理到 \(m=50\)。
记 \(A_{i,j}\) 表示使用 \(i\) 个格子,最左边是 \(j\) 且 \(j\) 不会被合并的概率,那么 \(A_{i,j}=a_{i-1,j}\times (1-a_{i,j})\)。
设 \(f_{i,j}\) 表示最右边 \(i\) 个格子的第一个数是 \(j\) 的期望和。
不难发现,最终的序列中,对于相邻的两个数 \(i,j\),要么 \(i=1\),要么 \(i>j\)。
当 \(j\neq 1\) 时,\(f_{i,j}=\dfrac{\sum_{k=1}^{j-1}f_{i-1,k}\times A_{i-1,k}}{\sum_{k=1}^{j-1}A_{i-1,k}} +j\quad (j\neq 1)\)
当 \(j=1\) 时,第一个数是 \(1\),插入的第二个数一定是 \(2\)
设 \(b_{i,j}\) 表示使用 \(i\) 个格子,第一次插入的数是 \(2\),最左边是 \(j\) 的概率,转移 \(b_{i,j}=a_{i-1,j-1}\times b_{i-1,j}\)。
同理,记 \(B_{i,j}\) 表示 \(j\) 不会被合并的概率,\(B_{i,j}=b_{i,j}\times (1-a_{i-1,j})\)。
那么 \(f_{i,j}=\dfrac{\sum_{k=2}^mf_{i-1,k}\times B_{i-1, k}}{\sum_{k=2}^mB_{i-1, k}}\quad(j=1)\)
最终答案是 \(\sum_{i=1}^nA_{n,i}\times f_{n,i}\)
对于 \(n\le 50\) 可以直接暴力算
否则,考虑矩阵快速幂,由于太麻烦,所以直接借鉴 cyffff 的题解 的图(
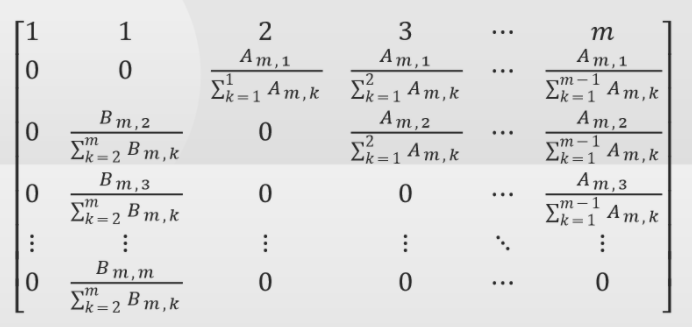
然后就可以用预处理的 \(1\times 50\) 的 \(f\) 数组愉快的转移了
Code
#include <bits/stdc++.h>
#define ll long long
#define db double
#define gc getchar
#define pc putchar
#define pb push_back
using namespace std;
namespace IO
{
template <typename T>
void read(T &x)
{
x = 0; bool f = 0; char c = gc();
while(!isdigit(c)) f |= c == '-', c = gc();
while(isdigit(c)) x = x * 10 + c - '0', c = gc();
if(f) x = -x;
}
template <typename T, typename ...Args>
void read(T &x, Args &...args) {read(x), read(args...);}
template <typename T>
void write(T x)
{
if(x < 0) pc('-'), x = -x;
if(x > 9) write(x / 10);
pc('0' + x % 10);
}
}
using namespace IO;
const int N = 55;
int n, m = 50;
db p, a[N][N], b[N][N];
db f[N][N];
struct Matrix
{
db mat[N][N];
Matrix() {memset(mat, 0, sizeof(mat));}
Matrix operator * (const Matrix &b) const
{
Matrix a;
for(int i = 0; i <= m; i++)
for(int j = 0; j <= m; j++)
for(int k = 0; k <= m; k++)
a.mat[i][j] += mat[i][k] * b.mat[k][j];
return a;
}
Matrix operator ^ (int b)
{
Matrix a, res;
memcpy(a.mat, mat, sizeof(mat));
for(int i = 0; i <= m; i++) res.mat[i][i] = 1;
for(; b; a = a * a, b >>= 1)
if(b & 1) res = res * a;
return res;
}
} A, B;
int main()
{
read(n, p); p /= 1e9;
a[1][1] = p, a[1][2] = b[1][2] = 1 - p;
for(int i = 2; i <= m; i++)
{
a[i][1] = p, a[i][2] = 1 - p + p * p, b[i][2] = 1 - p;
for(int j = 3; j <= m; j++)
{
a[i][j] = a[i - 1][j - 1] * a[i][j - 1];
b[i][j] = a[i - 1][j - 1] * b[i][j - 1];
}
}
for(int i = m; i >= 1; i--)
for(int j = 1; j <= m; j++)
{
a[i][j] *= (1.0 - a[i - 1][j]);
b[i][j] *= (1.0 - a[i - 1][j]);
}
f[1][1] = 1, f[1][2] = 2;
for(int i = 2; i <= m; i++)
{
db sum = 0;
for(int j = 2; j <= m; j++)
f[i][1] += f[i - 1][j] * b[i - 1][j], sum += b[i - 1][j];
f[i][1] = f[i][1] / sum + 1;
for(int j = 2; j <= m; j++)
{
sum = 0;
for(int k = 1; k < j; k++)
f[i][j] += f[i - 1][k] * a[i - 1][k], sum += a[i - 1][k];
f[i][j] = f[i][j] / sum + j;
}
}
if(n <= m)
{
db ans = 0;
for(int i = 1; i <= m; i++)
ans += a[n][i] * f[n][i];
printf("%.8lf\n", ans);
return 0;
}
A.mat[0][0] = 1;
for(int i = 1; i <= m; i++) A.mat[0][i] = f[m][i];
db sum = 0;
B.mat[0][0] = B.mat[0][1] = 1;
for(int i = 2; i <= m; i++) B.mat[i][1] += b[m][i], sum += b[m][i];
for(int i = 2; i <= m; i++) B.mat[i][1] /= sum;
for(int j = 2; j <= m; j++)
{
sum = 0;
for(int i = 1; i < j; i++)
B.mat[i][j] += a[m][i], sum += a[m][i];
for(int i = 1; i < j; i++) B.mat[i][j] /= sum;
B.mat[0][j] = j;
}
A = A * (B ^ (n - m));
db ans = 0;
for(int i = 1; i <= m; i++)
ans += a[m][i] * A.mat[0][i];
printf("%.8lf\n", ans);
return 0;
}
// A.S.
CF446D DZY Loves Games
发现 \(k\) 巨大,不难想到矩阵快速幂优化,经典利用邻接矩阵,每乘一次相当于走一步,所以只需要求出任意两个有陷阱的房间之间走到的概率。
考虑先计算任意两个房间不经过陷阱的概率,设 \(f_{i,j}\) 表示从 \(i\) 走到 \(j\) 的概率,显然
若第 \(i\) 个房间有陷阱 \(f_{i,i} = 1,f_{i,j} =0(j\neq i)\)
这可以高斯消元,但是我们要求解到每个陷阱的概率,不能暴力对每个陷阱列方程计算,但我们发现每个陷阱的区别仅仅是常数项,方程都是一样的,所以将所有陷阱都加到后面同时求解即可。
然后同理可得两两陷阱之间的概率,最后矩阵快速幂
Code
#include <bits/stdc++.h>
#define ll long long
#define db double
#define gc getchar
#define pc putchar
#define pb push_back
using namespace std;
namespace IO
{
template <typename T>
void read(T &x)
{
x = 0; bool f = 0; char c = gc();
while(!isdigit(c)) f |= c == '-', c = gc();
while(isdigit(c)) x = x * 10 + c - '0', c = gc();
if(f) x = -x;
}
template <typename T, typename ...Args>
void read(T &x, Args &...args) {read(x), read(args...);}
template <typename T>
void write(T x)
{
if(x < 0) pc('-'), x = -x;
if(x > 9) write(x / 10);
pc('0' + x % 10);
}
}
using namespace IO;
const int N = 505;
int n, m, k, tot, id[N];
int g[N][N], deg[N];
bool flag[N];
db a[N][N << 1];
void Gauss(int n, int m)
{
for(int i = 1; i <= n; i++)
{
for(int j = i + 1; j <= n && a[i][i] == 0; j++)
if(a[j][i]) swap(a[i], a[j]);
for(int j = m; j >= i; j--) a[i][j] /= a[i][i];
for(int j = 1; j <= n; j++)
{
if(i == j) continue;
db t = a[j][i] / a[i][i];
for(int k = i; k <= m; k++)
a[j][k] -= a[i][k] * t;
}
}
return;
}
struct Matrix
{
int n;
db mat[105][105];
Matrix() {memset(mat, 0, sizeof(mat));}
void init() {for(int i = 1; i <= n; i++) mat[i][i] = 1;}
Matrix operator * (const Matrix &b) const
{
Matrix c; c.n = n;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
for(int k = 1; k <= n; k++)
c.mat[i][j] += mat[i][k] * b.mat[k][j];
return c;
}
Matrix operator ^ (int b)
{
Matrix a, res;
res.n = n, res.init();
a.n = n, memcpy(a.mat, mat, sizeof(mat));
while(b)
{
if(b & 1) res = res * a;
a = a * a, b >>= 1;
}
return res;
}
} A, B;
int main()
{
read(n, m, k);
for(int i = 1; i <= n; i++)
{
read(flag[i]);
if(flag[i]) id[++tot] = i;
}
for(int i = 1, u, v; i <= m; i++)
read(u, v), g[u][v]++, g[v][u]++, deg[u]++, deg[v]++;
for(int i = 1; i <= n; i++)
{
if(!flag[i]) {
for(int j = 1; j <= n; j++) a[i][j] = (db)g[i][j] / deg[i];
a[i][i] = -1;
} else {
int j = lower_bound(id + 1, id + 1 + tot, i) - id;
a[i][i] = a[i][n + j] = 1;
}
}
Gauss(n, n + tot);
A.n = B.n = tot;
for(int i = 1; i <= tot; i++) A.mat[1][i] = a[1][n + i];
for(int i = 1; i <= tot; i++)
for(int j = 1; j <= tot; j++)
{
for(int k = 1; k <= n; k++)
B.mat[i][j] += (db)g[id[i]][k] * a[k][n + j];
B.mat[i][j] /= deg[id[i]];
}
A = A * (B ^ (k - 2));
printf("%.6lf\n", A.mat[1][tot]);
return 0;
}
// A.S.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号