Luogu P4478 [BJWC2018]上学路线 题解
先来看看数据范围,就发现可以骗到分。
\(\bold{40pts:}\)
测试点1、2:\(n,m≤1000\),直接 \(O(nm)DP\)。
测试点3、4:没有施工路口,直接 \(C_{n+m}^n\) 求总方案数,然后因为 \(P\) 是质数,所以用逆元取模即可。
\(\bold{60pts:}\)
测试点5、6:因为 \(P\) 不是质数,所以把 \(P\) 分解成几个质数的乘积,分别算出 \(C_{n+m}^n\) 对每个质数取模的结果,然后用 中国剩余定理\((CRT)\) 合并求解(中国剩余定理下面会讲)。
以上就是考场上的骗分思路。
\(\bold{100pts:}\)
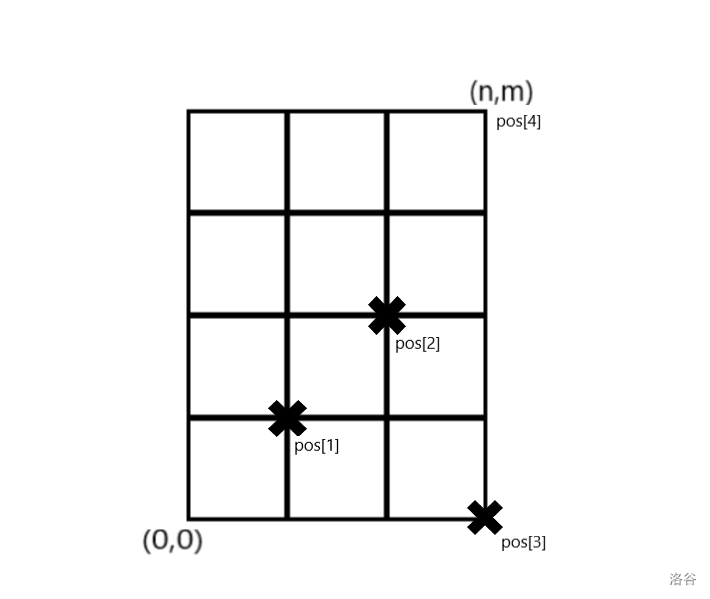
把每个施工路口的坐标存进 \(pos\) 结构体数组,再把 \((n,m)\) 存进 \(pos_{t+1}\),然后将 \(pos\) 按 \(x\) 从小到大排序,如果 \(x\) 相等,就按 \(y\) 从小到大排序。
用 \(f_i\) 表示从 \((0,0)\) 到 \((pos_i.x,pos_i.y)\) 并且不经过其他施工路口的方案数,然后大力推式子:
这里为了方便表示,将 \((pos_i.x,pos_i.y)\) 改为 \((x_i,y_i)\)
其中,
第一项表示从 \((0,0)\) 到 \((x_i,y_i)\) 的总方案数。
第二项表示所有所有符合要求的 \(j\) 从 \((0,0)\) 到 \((x_i,y_i)\) 且不经过其他施工路口的方案数 × 从\((x_j,y_j)\) 到 \((x_i,y_i)\) 的方案数的和。
显然,\(j\) 的条件是 \(x_j\le x_i,y_j\le y_i\)。
由于已经将 \(pos\) 数组排了序,所以式子中 \(j\) 的范围可以缩小到 \(i-1\) :
举个例子(样例):
已知 \(f_1=2\) 求 \(f_2:\)
其余同理。
最后输出 \(f_t\) 即可。
至此,本题的主体思路已经讲完了。
接下来考虑怎么计算 \(C_n^m\bmod P\)。
因为 \(P\) 不一定是质数,所以不能直接用逆元取模。
当 \(P\) 是质数的时:
直接用 \(Lucas\) 即可。
\(C_n^m=C_{n\bmod{p}}^{m\bmod{p}}×C_{n/p}^{m/p}\bmod{p}\)
当 \(P\) 不是质数时:
如何处理上面已经提到了,就是把 \(P\) 分解成几个质数的积,存进 \(p\) 数组,再用 \(CRT\) 合并。
先介绍一下 \(CRT:\)
设 \(m_1,m_2,...,m_n\) 是两两互质的整数,\(m=∏_{i=1}^nm_i\),\(M_i=\dfrac{m}{m_i}\),\(t_i\)是线性方程\(M_it_i≡1(mod\ m_i)\) 的一个解(也就是逆元)。
对于任意的 \(n\) 个整数 \(a_1,a_2,...,a_n,\) 方程组
\(\begin{cases} x≡a_1\ (\bmod{m_1})&\\ x≡a_2\ (\bmod{m_2})&\\ ...\ &\\ x≡a_n\ (\bmod{m_n}) \end{cases}\)
有整数解,解为 \(x=\sum_{i=1}^na_iM_it_i\)。
证明请左转自行百度。
本题中 \(P=1019663265=3×5×6793×10007\)
令 \(p_1=3,\ p_2=5,\ p_3=6793,\ p_4=10007\),显然它们两两互质,符合上述 \(CRT\) 中的 \(m\) 数组。
\(a_i=C_n^m \bmod p_i\) 这里就可以逆元了
已经能求出 \(C_n^m\bmod{P}\) 了。
然后再用 \(DP\) 转移出最后的结果。
复杂度 \(O(T^2\log n)\)
上代码:
#include <bits/stdc++.h>
#define ll long long
#define db double
#define gc getchar
#define pc putchar
using namespace std;
namespace IO
{
template <typename T>
void read(T &x)
{
x = 0; bool f = 0; char c = gc();
while(!isdigit(c)) f |= c == '-', c = gc();
while(isdigit(c)) x = x * 10 + c - '0', c = gc();
if(f) x = -x;
}
template <typename T>
void write(T x)
{
if(x < 0) pc('-'), x = -x;
if(x > 9) write(x / 10);
pc('0' + x % 10);
}
}
using namespace IO;
const int N = 1e6 + 5;
struct node
{
int x, y;
}pos[210];
int n, m, t, P, tp;
int f[210], g[5], p[5], mul[5], fac[5][N], invm[5], inv[5][N];
inline bool cmp(node a, node b)
{
return a.x == b.x ? a.y < b.y : a.x < b.x;
}
inline int power(int a, int b, int p)
{
int ret = 1;
a %= p;
while(b)
{
if(b & 1) ret = 1ll * ret * a % p;
a = 1ll * a * a % p, b >>= 1;
}
return ret;
}
inline int C(int a, int b, int i) //C(a, b) % i
{
if(a < b) return 0;
if(!b || a == b) return 1;
if(a < p[i] && b < p[i]) return 1ll * fac[i][a] * inv[i][b] % p[i] * inv[i][a - b] % p[i];
return 1ll * C(a % p[i], b % p[i], i) * C(a / p[i], b / p[i], i) % p[i];
}
inline int CRT(int a, int b) //中国剩余定理
{
if(!tp) return C(a, b, 0); //P为质数时直接返回C(a,b)%p[0]
int ret = 0;
for(int i = 1; i <= 4; i++) g[i] = C(a, b, i); //g[i]=C(a,b)%p[i]
for(int i = 1; i <= 4; i++) ret = (ret + 1ll * g[i] * mul[i] % P * invm[i] % P) % P;
return ret;
}
int main()
{
read(n), read(m), read(t), read(P);
for(int i = 1; i <= t; i++)
read(pos[i].x), read(pos[i].y);
pos[++t] = (node) {n, m}; //将(n,m)加到pos[t+1]
sort(pos + 1, pos + 1 + t, cmp); //排序
if(P == 1e6 + 3) p[0] = P; //如果P是质数,存到p[0]
else p[1] = 3, p[2] = 5, p[3] = 6793, p[4] = 10007, tp = 1; //否则,分解成4个质数,并且tp=1,表示P不是质数
//预处理
if(tp) //如果P不是质数
{
for(int i = 1; i <= 4; i++)
{
mul[i] = P / p[i]; //CRT 中的 m 数组
invm[i] = power(mul[i], p[i] - 2, p[i]); //mul[i] % p[i] 的逆元
fac[i][0] = 1; //0! % p[i]
for(int j = 1; j < p[i]; j++)
fac[i][j] = 1ll * fac[i][j - 1] * j % p[i]; //j! % p[i]
inv[i][p[i] - 1] = power(fac[i][p[i] - 1], p[i] - 2, p[i]); //(p[i]-1)! % p[i] 的逆元
for(int j = p[i] - 1; j >= 1; j--)
inv[i][j - 1] = 1ll * inv[i][j] * j % p[i]; //逆元的递推
}
}
else
{
//同上,只是少一层循环,因为只有一个质数
fac[0][0] = 1;
for(int i = 1; i < P; i++)
fac[0][i] = 1ll * fac[0][i - 1] * i % P;
inv[0][P - 1] = power(fac[0][P - 1], P - 2, P);
for(int i = P - 1; i >= 1; i--)
inv[0][i - 1] = 1ll * inv[0][i] * i % P;
}
for(int i = 1; i <= t; i++) {
f[i] = CRT(pos[i].x + pos[i].y, pos[i].x); //从(0,0)到(pos[i].x,pos[i].y)的总方案数
//减去经过其他施工路口的方案数
for(int j = 1; j < i; j++)
if(pos[j].x <= pos[i].x && pos[j].y <= pos[i].y)
f[i] = (f[i] - 1ll * f[j] * CRT(pos[i].x - pos[j].x + pos[i].y - pos[j].y, pos[i].x - pos[j].x) % P + P) % P;
}
write(f[t]), pc('\n');
return 0;
}
// A.S.
题外话:
我在写这篇题解的时候,浏览器突然就未响应了,所以就重新写了一遍 qwq,建议大家如果没有 typora 或 vscode 可以先在云剪贴板上写好了复制过来。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号