使用tensorflow实现机器学习中的线性拟合
使用tensorflow实现机器学习中的线性拟合
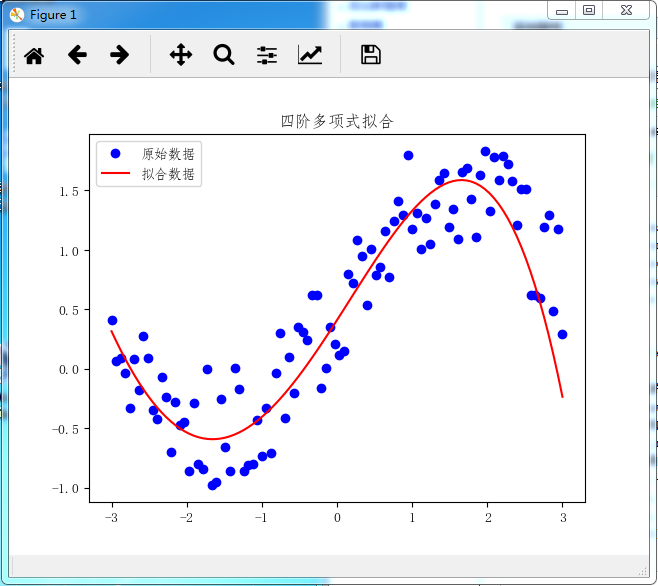
这个例子是模拟的单变量线性回归,通过提高单变量的阶数来增加特征数量,例如:4阶相当于分解为四个特征
这种思想同样适用于多变量线性回归
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['FangSong'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False# 用来正常显示负号
plt.title('四阶多项式拟合')
#数据准备
n_samples =100
#数据集
X = np.linspace(-3, 3, n_samples)
#数据集标签,需要拟合的结果
Y = np.sin(X) + np.random.uniform(0,1,n_samples)
#静态图定义
mg = tf.Graph()
with mg.as_default():
#占位
xs = tf.placeholder(dtype=tf.float32,name='xs')
ys = tf.placeholder(dtype=tf.float32,name='ys')
#需要训练的权重变量
w1 = tf.Variable(tf.random_normal([1]),name='w1')
w2 = tf.Variable(tf.random_normal([1]),name='w2')
w3 = tf.Variable(tf.random_normal([1]),name='w3')
w4 = tf.Variable(tf.random_normal([1]),name='w4')
b = tf.Variable(tf.zeros(1),name='b')
#多项式公式
my_pred = []
my_pred.append(tf.multiply(w1,xs))
my_pred.append(tf.multiply(w2,tf.pow(xs,2)))
my_pred.append(tf.multiply(w3,tf.pow(xs,3)))
my_pred.append(tf.multiply(w4,tf.pow(xs,4)))
y_pred = tf.add(tf.add_n(my_pred), b)
#损失函数:使用样本方差
loss = tf.reduce_sum(tf.pow(y_pred-ys, 2)) / (len(X)-1)
#学习率,其实就是用多大的步进持续学习
lr = 0.01
#学习的轮数
epochs = 1000
#使用梯度下降法优化
optimizer = tf.train.GradientDescentOptimizer(learning_rate=lr).minimize(loss)
with tf.Session(graph=mg) as sess:
sess.run(tf.global_variables_initializer())
for epoch in range(epochs):
total_loss = 0
for x,y in zip(X,Y):
_,tmp_loss = sess.run([optimizer,loss],feed_dict={xs:x,ys:y})
total_loss += tmp_loss
if epoch%10 == 0:
print('epoch{:} the loss {:}'.format(epoch,total_loss))
#获取系统优化结果
mgw1,mgw2,mgw3,mgw4,mgb = sess.run([w1,w2,w3,w4,b])
#session中的变量自动转换为全局变量
print(mgw1,mgw2,mgw3,mgw4,mgb)
#最终的拟合函数
YY= X*mgw1 + X**2*mgw2 + X**3*mgw3 + X**4*mgw4 + mgb
plt.plot(X, Y, 'bo', label='原始数据')
plt.plot(X, YY, 'r', label='拟合数据')
plt.legend()
plt.show()