ARC089D ColoringBalls 题解
考虑最后哪些颜色序列可以被得到。
先将相邻的相同颜色缩起来。这不会影响可达性。接着,\(\texttt{w}\) 可以视作分隔符,因为其一定没有被染过色。
现在整个序列被分成了 \(m\) 个连续段,且连续段内部相邻的颜色不同。设第 \(i\) 个连续段有 \(c_i\) 个 \(\texttt{b}\),考虑如何操作得到该连续段。
- 当 \(c_i=0\),显然需要 \(\texttt{r}\) 一次操作;
- 当 \(c_i=1\),显然需要 \(\texttt{r}\)\(\texttt{b}\) 两次操作;
- 当 \(c_i \ge 2\),共需要 \(c_i+2\) 次操作。前两次操作依然是 \(\texttt{r}\)\(\texttt{b}\),但后面 \(c_i\) 次操作居然是 \(\texttt{r}\)\(\texttt{b}\) 随便!如:要想得到 \(\texttt{rbrbr}\),操作序列为 \(\texttt{rbbr}, \texttt{rbrr}, \texttt{rbbb}, \texttt{rbrb}\) 都是可以的。
以上读者自证不难。
那么 check 一个颜色序列能否被得到就很简单了:缩成连续段以后按 \(\texttt{b}\) 的数量从大到小排序,然后分配操作序列:先把最前面 \(m\) 个 \(\texttt{r}\) 依次给每个连续段都分配一个,然后将所有 \(c_i \ge 1\) 的连续段贪心地找到先前分配的 \(\texttt{r}\) 后第一个 \(\texttt{b}\) 并占用,最后将所有 \(c_i \ge 2\) 的连续段贪心地占用先前分配的 \(\texttt{b}\) 后前 \(c_i\) 个还没有被占用的操作。如果找不到,这个颜色序列就不合法。
但是,我们仍然不可能枚举所有的连续段的 \(c_i\)。不过,我们发现连续段的 \(c_i\) 的次序是无关紧要的,所以类似划分数那样爆搜,然后用多重集排列计算即可。注意到一个有 \(c_i\) 个 \(\texttt{b}\) 的连续段长度至少为 \([c_i=0]+[c_i \ge 1](2c_i-1)\),因此方案数较少,为划分数级别。
最后,由于我们现在计算的是缩完相同颜色后的方案,我们还需要将其扩展至长度为 \(n\)。令 \(f(x)\) 表示有 \(x\) 个 \(\texttt{b}\) 的连续段长度的最小值,即 \(f(x)=[x=0]+[x \ge 1](2x-1)\)。则现在已经填了 \(A=m-1+\sum_{i=1}^m f(c_i)\) 个位置(\(m-1\) 是因为相邻两个连续段之间至少有一个 \(\texttt{w}\)),剩下 \(n-A\) 个位置尚未分配颜色。
考虑将未分配颜色的位置插入空隙中。一个有 \(c_i\) 个 \(\texttt{b}\) 的连续段有 \(2c_i+1\) 个空隙,而相邻两个连续段之间也有 1 个空隙以插入 \(\texttt{w}\)。如图:
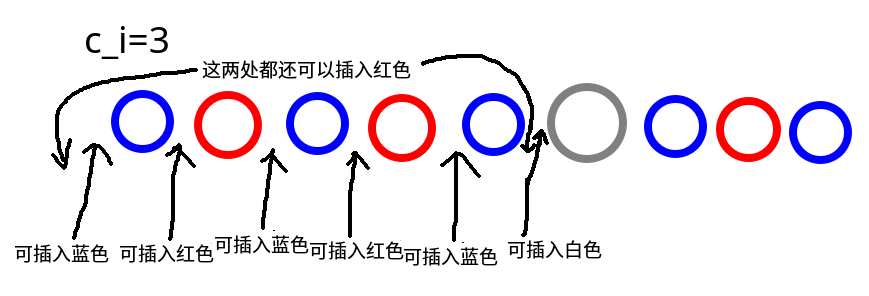
由于第 1 段前面还可以插入 \(\texttt{w}\),共 \(B=m+1+\sum_{i=1}^m (2c_i+1)\) 个空隙。用插板法将 \(n-A\) 个球分配到这些空隙中,方案数为:
于是就做完了。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef vector<int> vi;
typedef pair<int,int> pii;
template<typename T>
inline T read(){
T x=0,f=0;char ch=getchar();
while(!isdigit(ch)) f|=(ch=='-'),ch=getchar();
while(isdigit(ch)) x=x*10+(ch^48),ch=getchar();
return f?-x:x;
}
#define rdi read<int>
#define rdll read<ll>
#define fi first
#define se second
#define pb push_back
#define mp make_pair
const int N=100010,K=75,MOD=1e9+7;
int n,k;
char s[K];
ll ans;
ll qpow(ll x,ll y=MOD-2){
ll res=1;
while(y){
if(y&1) (res*=x)%=MOD;
(x*=x)%=MOD;y>>=1;
}
return res;
}
ll fac[N+K],faci[N+K];
void init(int n){
fac[0]=1;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%MOD;
faci[n]=qpow(fac[n]);
for(int i=n-1;i>=0;i--) faci[i]=faci[i+1]*(i+1)%MOD;
}
ll C(int x,int y){return fac[x]*faci[y]%MOD*faci[x-y]%MOD;}
int a[K],cnt;
bool vis[N];
int st[N];
bool check(int *a,int cnt){
int sum=-1;
for(int i=1;i<=cnt;i++) sum+=(!a[i]?1:2*a[i]-1)+1;
if(sum>n) return false;
for(int i=1;i<=k;i++) vis[i]=0;
int pos=1;
for(int i=cnt;i>=1;i--){
while(pos<=k&&(vis[pos]||s[pos]!='r')) pos++;
if(pos>k) return false;
vis[pos]=1,st[i]=pos;
}
pos=1;
for(int i=cnt;i>=1;i--){
if(a[i]){
pos=max(pos,st[i]);
while(pos<=k&&(vis[pos]||s[pos]!='b')) pos++;
if(pos>k) return false;
vis[pos]=1,st[i]=pos;
}
}
pos=1;
for(int i=cnt;i>=1;i--){
if(a[i]>1){
pos=max(pos,st[i]);
for(int j=1;j<a[i];j++){
while(pos<=k&&vis[pos]) pos++;
if(pos>k) return false;
vis[pos]=1;
}
}
}
return true;
}
ll calc(int *a,int cnt){
ll mul=1;
int sum=0,sum1=0;
for(int l=1;l<=cnt;){
int r=l;
while(r<=cnt&&a[l]==a[r]){
sum+=(!a[r]?1:2*a[r]-1)+1;
sum1+=a[r]*2+1,r++;
}
(mul*=faci[r-l])%=MOD,l=r;
}
(mul*=fac[cnt])%=MOD;
sum1+=cnt+1;
(mul*=C(n-sum+sum1,sum1-1))%=MOD;
return mul;
}
void dfs(int rest,int cnt,int lst=0){
if(cnt){
if(check(a,cnt)) ans+=calc(a,cnt);
else return;
}
for(int i=lst;i<=rest;i++) a[cnt+1]=i,dfs(rest-i-1,cnt+1,i);
}
int main(){
#ifdef LOCAL
freopen(".in","r",stdin);
freopen(".out","w",stdout);
#endif
n=rdi(),k=rdi();init(n+k+1);
scanf("%s",s+1);
dfs(k,0);ans=(ans+1)%MOD;
cout<<ans<<endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号