海量处理面试题
转自：http://www.cnblogs.com/sooner/archive/2013/08/18/3266545.html
何谓海量数据处理？
所谓海量数据处理，其实很简单，海量，海量，何谓海量，就是数据量太大，所以导致要么是无法在较短时间内迅速解决，要么是数据太大，导致无法一次性装入内存。
那解决办法呢?针对时间，我们可以采用巧妙的算法搭配合适的数据结构，如Bloom filter/Hash/bit-map/堆/数据库或倒排索引/trie/，针对空间，无非就一个办法：大而化小：分而治之/hash映射，你不是说规模太大嘛，那简单啊，就把规模大化为规模小的，各个击破不就完了嘛。
至于所谓的单机及集群问题，通俗点来讲，单机就是处理装载数据的机器有限(只要考虑cpu，内存，硬盘的数据交互)，而集群，机器有多辆，适合分布式处理，并行计算(更多考虑节点和节点间的数据交互)。
再者，通过本blog内的有关海量数据处理的文章，我们已经大致知道，处理海量数据问题，无非就是：
- 分而治之/hash映射 + hash统计 + 堆/快速/归并排序；
- 双层桶划分
- Bloom filter/Bitmap；
- Trie树/数据库/倒排索引；
- 外排序；
- 分布式处理之Hadoop/Mapreduce。
下面，本文第一部分、从set/map谈到hashtable/hash_map/hash_set，简要介绍下set/map/multiset/multimap，及hash_set/hash_map/hash_multiset/hash_multimap之区别(万丈高楼平地起，基础最重要)，而本文第二部分，则针对上述那6种方法模式结合对应的海量数据处理面试题分别具体阐述
第一部分、从set/map谈到hashtable/hash_map/hash_set
稍后本文第二部分中将多次提到hash_map/hash_set，下面稍稍介绍下这些容器，以作为基础准备。一般来说，STL容器分两种，
- 序列式容器(vector/list/deque/stack/queue/heap)，
- 关联式容器。关联式容器又分为set(集合)和map(映射表)两大类，以及这两大类的衍生体multiset(多键集合)和multimap(多键映射表)，这些容器均以RB-tree完成。此外，还有第3类关联式容器，如hashtable(散列表)，以及以hashtable为底层机制完成的hash_set(散列集合)/hash_map(散列映射表)/hash_multiset(散列多键集合)/hash_multimap(散列多键映射表)。也就是说，set/map/multiset/multimap都内含一个RB-tree，而hash_set/hash_map/hash_multiset/hash_multimap都内含一个hashtable。
所谓关联式容器，类似关联式数据库，每笔数据或每个元素都有一个键值(key)和一个实值(value)，即所谓的Key-Value(键-值对)。当元素被插入到关联式容器中时，容器内部结构(RB-tree/hashtable)便依照其键值大小，以某种特定规则将这个元素放置于适当位置。
包括在非关联式数据库中，比如，在MongoDB内，文档(document)是最基本的数据组织形式，每个文档也是以Key-Value（键-值对）的方式组织起来。一个文档可以有多个Key-Value组合，每个Value可以是不同的类型，比如String、Integer、List等等。
{ "name" : "July",
"sex" : "male",
"age" : 23 }
set/map/multiset/multimap
set，同map一样，所有元素都会根据元素的键值自动被排序，因为set/map两者的所有各种操作，都只是转而调用RB-tree的操作行为，不过，值得注意的是，两者都不允许两个元素有相同的键值。
不同的是：set的元素不像map那样可以同时拥有实值(value)和键值(key)，set元素的键值就是实值，实值就是键值，而map的所有元素都是pair，同时拥有实值(value)和键值(key)，pair的第一个元素被视为键值，第二个元素被视为实值。
至于multiset/multimap，他们的特性及用法和set/map完全相同，唯一的差别就在于它们允许键值重复，即所有的插入操作基于RB-tree的insert_equal()而非insert_unique()。
hash_set/hash_map/hash_multiset/hash_multimap
hash_set/hash_map，两者的一切操作都是基于hashtable之上。不同的是，hash_set同set一样，同时拥有实值和键值，且实质就是键值，键值就是实值，而hash_map同map一样，每一个元素同时拥有一个实值(value)和一个键值(key)，所以其使用方式，和上面的map基本相同。但由于hash_set/hash_map都是基于hashtable之上，所以不具备自动排序功能。为什么?因为hashtable没有自动排序功能。
至于hash_multiset/hash_multimap的特性与上面的multiset/multimap完全相同，唯一的差别就是它们hash_multiset/hash_multimap的底层实现机制是hashtable(而multiset/multimap，上面说了，底层实现机制是RB-tree)，所以它们的元素都不会被自动排序，不过也都允许键值重复。
所以，综上，说白了，什么样的结构决定其什么样的性质，因为set/map/multiset/multimap都是基于RB-tree之上，所以有自动排序功能，而hash_set/hash_map/hash_multiset/hash_multimap都是基于hashtable之上，所以不含有自动排序功能，至于加个前缀multi_无非就是允许键值重复而已。
此外，
- 关于什么hash，请看blog内此篇文章：http://blog.csdn.net/v_JULY_v/article/details/6256463；
- 关于红黑树，请参看blog内系列文章：http://blog.csdn.net/v_july_v/article/category/774945，
- 关于hash_map的具体应用：http://blog.csdn.net/sdhongjun/article/details/4517325，关于hash_set：http://blog.csdn.net/morewindows/article/details/7330323。
OK，接下来，请看本文第二部分、处理海量数据问题之六把密匙。
第二部分、处理海量数据问题之六把密匙
密匙一、分而治之/Hash映射 + Hash统计 + 堆/快速/归并排序
1、海量日志数据，提取出某日访问百度次数最多的那个IP。
首先是这一天，并且是访问百度的日志中的IP取出来，逐个写入到一个大文件中。注意到IP是32位的，最多有个2^32个IP。同样可以采用映射的方法，比如模1000，把整个大文件映射为1000个小文件，再找出每个小文中出现频率最大的IP（可以采用hash_map进行频率统计，然后再找出频率最大的几个）及相应的频率。然后再在这1000个最大的IP中，找出那个频率最大的IP，即为所求。
或者如下阐述（雪域之鹰）：
算法思想：分而治之+Hash
1.IP地址最多有2^32=4G种取值情况，所以不能完全加载到内存中处理；
2.可以考虑采用“分而治之”的思想，按照IP地址的Hash(IP)%1024值，把海量IP日志分别存储到1024个小文件中。这样，每个小文件最多包含4MB个IP地址；
3.对于每一个小文件，可以构建一个IP为key，出现次数为value的Hash_map，同时记录当前出现次数最多的那个IP地址；
4.可以得到1024个小文件中的出现次数最多的IP，再依据常规的排序算法得到总体上出现次数最多的IP；
分析：有的网友提出以下疑问：我感觉这个值不应该是要求的那个。因为可能某一个ip在某一个小文件中可能出现频率很高，但是在其他小文件中可能没出现几次，即分布不均，但因为某一个小文件中特别多而被选出来了；而另一个ip可能在每个小文件中都不是出现最多的，但是它在每个文件中都出现很多次，即分布均匀，因此非常有可能它就是总的出现次数最多的，但是因为在每个小文件中出现的次数都不是最多的而被刷掉了。所以我感觉上面的方案不行。
这就考虑到“分而治之”中的“分”到底怎么分。。在第二步中我们提到按照IP地址的Hash(IP)%1024的值，将海量IP日志分别存储到1024个小文件中。。这样就会致使相似的IP或者同一IP被分到同一小文件中。。满足分而治之的要求。。故不存在分布均匀情况。。
还有一位网友给出了具体的方法：计数法（原理同上：分而治之）
假设一天之内某个IP访问百度的次数不超过40亿次,则访问次数可以用unsigned表示.用数组统计出每个IP地址出现的次数, 即可得到访问次数最大的IP地址。
IP地址是32位的二进制数,所以共有N=2^32=4G个不同的IP地址, 创建一个unsigned count[N];的数组,即可统计出每个IP的访问次数,而sizeof(count) == 4G*4=16G, 远远超过了32位计算机所支持的内存大小,因此不能直接创建这个数组.下面采用划分法解决这个问题.
假设允许使用的内存是512M, 512M/4=128M 即512M内存可以统计128M个不同的IP地址的访问次数.而N/128M =4G/128M = 32 ,所以只要把IP地址划分成32个不同的区间,分别统计出每个区间中访问次数最大的IP, 然后就可以计算出所有IP地址中访问次数最大的IP了.
因为2^5=32, 所以可以把IP地址的最高5位作为区间编号, 剩下的27为作为区间内的值,建立32个临时文件,代表32个区间,把相同区间的IP地址保存到同一的临时文件中.
例如:
ip1=0x1f4e2342
ip1的高5位是id1 = ip1 >>27 = 0x11 = 3
ip1的其余27位是value1 = ip1 &0x07ffffff = 0x074e2342
所以把 value1 保存在tmp3文件中。
由id1和value1可以还原成ip1, 即 ip1 =(id1<<27)|value1
按照上面的方法可以得到32个临时文件,每个临时文件中的IP地址的取值范围属于[0-128M),因此可以统计出每个IP地址的访问次数.从而找到访问次数最大的IP地址
程序源码:
#include <fstream>
#include <iostream>
#include <ctime>
using namespace std;
#define N 32 //临时文件数
#define ID(x) (x>>27) //x对应的文件编号
#define VALUE(x) (x&0x07ffffff) //x在文件中保存的值
#define MAKE_IP(x,y) ((x<<27)|y) //由文件编号和值得到IP地址.
#define MEM_SIZE 128*1024*1024 //需分配内存的大小为 MEM_SIZE*sizeof(unsigned)
char* data_path="D:/test/ip.dat"; //ip数据
//产生n个随机IP地址
void make_data(const int& n)
{
ofstream out(data_path,ios::out|ios::binary);
srand((unsigned)(time(NULL)));
if (out)
{
for (int i=0; i<n; ++i)
{
unsigned val=unsigned(rand());
val = (val<<24)|val; //产生unsigned类型的随机数
out.write((char *)&val,sizeof (unsigned));
}
}
}
//找到访问次数最大的ip地址
int main()
{
//make_data(100); //
make_data(100000000); //产生测试用的IP数据
fstream arr[N];
for (int i=0; i<N; ++i) //创建N个临时文件
{
char tmp_path[128]; //临时文件路径
sprintf(tmp_path,"D:/test/tmp%d.dat",i);
arr[i].open(tmp_path, ios::trunc|ios::in|ios::out|ios::binary); //打开第i个文件
if( !arr[i])
{
cout<<"open file"<<i<<"error"<<endl;
}
}
ifstream infile(data_path,ios::in|ios::binary); //读入测试用的IP数据
unsigned data;
while(infile.read((char*)(&data), sizeof(data)))
{
unsigned val=VALUE(data);
int key=ID(data);
arr[ID(data)].write((char*)(&val), sizeof(val)); //保存到临时文件件中
}
for(unsigned i=0; i<N; ++i)
{
arr[i].seekg(0);
}
unsigned max_ip = 0; //出现次数最多的ip地址
unsigned max_times = 0; //最大只出现的次数
//分配512M内存,用于统计每个数出现的次数
unsigned *count = new unsigned[MEM_SIZE];
for (unsigned i=0; i<N; ++i)
{
memset(count, 0, sizeof(unsigned)*MEM_SIZE);
//统计每个临时文件件中不同数字出现的次数
unsigned data;
while(arr[i].read((char*)(&data), sizeof(unsigned)))
{
++count[data];
}
//找出出现次数最多的IP地址
for(unsigned j=0; j<MEM_SIZE; ++j)
{
if(max_times<count[j])
{
max_times = count[j];
max_ip = MAKE_IP(i,j); // 恢复成原ip地址.
}
}
}
delete[] count;
unsigned char *result=(unsigned char *)(&max_ip);
printf("出现次数最多的IP为:%d.%d.%d.%d,共出现%d次",
result[0], result[1], result[2], result[3], max_times);
}
运行结果：
2、寻找热门查询
搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有一千万个记录，这些查询串的重复读比较 高，虽然总数是1千万，但是如果去除重复和，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就越热门。请你统计最热门的10个查询 串，要求使用的内存不能超过1G。
(1) 请描述你解决这个问题的思路；
(2) 请给出主要的处理流程，算法，以及算法的复杂度。
方案一：
分析：此问题的解决分为以下俩个步骤：
第一步：Query统计
Query统计有以下俩个方法，可供选择：
1）、直接排序法
首先我们最先想到的的算法就是排序了，首先对这个日志里面的所有Query都进行排序，然后再遍历排好序的Query，统计每个Query出现的次数了。
但是题目中有明确要求，那就是内存不能超过1G，一千万条记录，每条记录是255Byte，很显然要占据2.375G内存，这个条件就不满足要求了。
让我们回忆一下数据结构课程上的内容，当数据量比较大而且内存无法装下的时候，我们可以采用外排序的方法来进行排序，这里我们可以采用归并排序，因为归并排序有一个比较好的时间复杂度O(NlgN)。
排完序之后我们再对已经有序的Query文件进行遍历，统计每个Query出现的次数，再次写入文件中。
综合分析一下，排序的时间复杂度是O(NlgN)，而遍历的时间复杂度是O(N)，因此该算法的总体时间复杂度就是O(N+NlgN)=O（NlgN）。
2）、Hash Table法
在第1个方法中，我们采用了排序的办法来统计每个Query出现的次数，时间复杂度是NlgN，那么能不能有更好的方法来存储，而时间复杂度更低呢？
题目中说明了，虽然有一千万个Query，但是由于重复度比较高，因此事实上只有300万的Query，每个Query255Byte，因此我们可以考虑把他们都放进内存中去，而现在只是需要一个合适的数据结构，在这里，Hash Table绝对是我们优先的选择，因为Hash Table的查询速度非常的快，几乎是O(1)的时间复杂度。
那么，我们的算法就有了：维护一个Key为Query字串，Value为该Query出现次数的HashTable，每次读取一个Query，如果该字串不在Table中，那么加入该字串，并且将Value值设为1；如果该字串在Table中，那么将该字串的计数加一即可。最终我们在O(N)的时间复杂度内完成了对该海量数据的处理。
本方法相比算法1：在时间复杂度上提高了一个数量级，为O（N），但不仅仅是时间复杂度上的优化，该方法只需要IO数据文件一次，而算法1的IO次数较多的，因此该算法2比算法1在工程上有更好的可操作性。
第二步：找出Top 10
算法一：普通排序
我想对于排序算法大家都已经不陌生了，这里不在赘述，我们要注意的是排序算法的时间复杂度是NlgN，在本题目中，三百万条记录，用1G内存是可以存下的。
算法二：部分排序
题目要求是求出Top 10，因此我们没有必要对所有的Query都进行排序，我们只需要维护一个10个大小的数组，初始化放入10个Query，按照每个Query的统计次数由大到小排序，然后遍历这300万条记录，每读一条记录就和数组最小一个Query对比，如果小于这个Query，那么继续遍历，否则，将数组中最后一条数据淘汰，加入当前的Query（并寻找最小元素）。最后当所有的数据都遍历完毕之后，那么这个数组中的10个Query便是我们要找的Top10了。
不难分析出，这样，算法的最坏时间复杂度是N*K， 其中K是指top多少。
算法三：堆
在算法二中，我们已经将时间复杂度由NlogN优化到NK，不得不说这是一个比较大的改进了，可是有没有更好的办法呢？
分析一下，在算法二中，每次比较完成之后，需要的操作复杂度都是K，因为要把元素插入到一个线性表之中，而且采用的是顺序比较。这里我们注意一下，该数组是有序的，一次我们每次查找的时候可以采用二分的方法查找，这样操作的复杂度就降到了logK，可是，随之而来的问题就是数据移动，因为移动数据次数增多了。不过，这个算法还是比算法二有了改进。
基于以上的分析，我们想想，有没有一种既能快速查找，又能快速移动元素的数据结构呢？回答是肯定的，那就是堆。
借助堆结构，我们可以在log量级的时间内查找和调整/移动。因此到这里，我们的算法可以改进为这样，维护一个K(该题目中是10)大小的小根堆，然后遍历300万的Query，分别和根元素进行对比。
思想与上述算法二一致，只是算法在算法三，我们采用了最小堆这种数据结构代替数组，把查找目标元素的时间复杂度有O（K）降到了O（logK）。
那么这样，采用堆数据结构，算法三，最终的时间复杂度就降到了N‘logK，和算法二相比，又有了比较大的改进。
总结：
至此，算法就完全结束了，经过上述第一步、先用Hash表统计每个Query出现的次数，O（N）；然后第二步、采用堆数据结构找出Top 10，N*O（logK）。所以，我们最终的时间复杂度是：O（N） + N'*O（logK）。（N为1000万，N’为300万）。
方案二：采用trie树，关键字域存该查询串出现的次数，没有出现为0。最后用10个元素的最小推来对出现频率进行排序。
3、有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。
分而治之 + hash统计 + 堆/快速排序这个套路，我们已经开始有了屡试不爽的感觉。下面，再拿几道再多多验证下。请看此第3题：又是文件很大，又是内存受限，咋办?还能怎么办呢?无非还是：
- 分而治之/hash映射：顺序读文件中，对于每个词x，取hash(x)%5000，然后按照该值存到5000个小文件（记为x0,x1,...x4999）中。这样每个文件大概是200k左右。如果其中的有的文件超过了1M大小，还可以按照类似的方法继续往下分，直到分解得到的小文件的大小都不超过1M。
- hash统计：对每个小文件，采用trie树/hash_map等统计每个文件中出现的词以及相应的频率。
- 堆/归并排序：取出出现频率最大的100个词（可以用含100个结点的最小堆），并把100个词及相应的频率存入文件，这样又得到了5000个文件。最后就是把这5000个文件进行归并（类似于归并排序）的过程了。
读者反馈@ylqndscylq：本文评论下，有读者ylqndscylq反应：每个小文件取前100会有问题。是否真如此，咱们先且看下一道题，第4题(稍后，我们将意识到，这第3题给出的算法有问题)。
有网友提出：呵呵
普通解法:分治，hash，归并，最大（小）堆，map reducer等算法，你的小内存导致了只能用时间换空间的做法， 比如多次的遍历，big set分裂成小set，使用磁盘索引等。
2B解法： lucene
文艺解法（ibm研究院提供）：基于priori algorithm.
http://rakesh.agrawal-family.com/papers/vldb94apriori.pdf
4、一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析。
方案1：这题是考虑时间效率。用trie树统计每个词出现的次数，时间复杂度是O(n*le)（le表示单词的平准长度）。然后是找出出现最频繁的前10个词，可以用堆来实现，前面的题中已经讲到了，时间复杂度是O(n*lg10)。所以总的时间复杂度，是O(n*le)与O(n*lg10)中较大的哪一个。
- 堆/归并排序：在每台电脑上求出TOP10，可以采用包含10个元素的堆完成（TOP10小，用最大堆，TOP10大，用最小堆）。比如求TOP10大，我们首先取前10个元素调整成最小堆，如果发现，然后扫描后面的数据，并与堆顶元素比较，如果比堆顶元素大，那么用该元素替换堆顶，然后再调整为最小堆。最后堆中的元素就是TOP10大。
- 求出每台电脑上的TOP10后，然后把这100台电脑上的TOP10组合起来，共1000个数据，再利用上面类似的方法求出TOP10就可以了。
a 49次b 50次c 2次d 1次
a 9次b 1次c 11次d 10次
方案1：在前面的题中，我们已经提到了，用一个含100个元素的最小堆完成。复杂度为O(100w*lg100)。
方案2：采用快速排序的思想，每次分割之后只考虑比轴大的一部分，知道比轴大的一部分在比100多的时候，采用传统排序算法排序，取前100个。复杂度为O(100w*100)。
算法如下：根据快速排序划分的思想
(1) 先对所有数据分成[a,b）b（b,d]两个区间，(b,d]区间内的数都是大于[a,b)区间内的数
(2) 对(b,d]重复(1)操作，直到最右边的区间个数小于100个。注意[a,b)区间不用划分
(3) 向左边的第一个区间取前100-n.n为已取出的元素个数。方法仍然是对其划分，取[c,d]区间。如果个数不够，继续(3)操作
(4) 有必要的话，对取出的100个数进行快速排序。over~
方案3：采用局部淘汰法。选取前100个元素，并排序，记为序列L。然后一次扫描剩余的元素x，与排好序的100个元素中最小的元素比，如果比这个最小的要大，那么把这个最小的元素删除，并把x利用插入排序的思想，插入到序列L中。依次循环，知道扫描了所有的元素。复杂度为O(100w*100)。
进一步：1亿数据找出最大的1w个
1. 分块法
解法：A. 采用分块法，将1亿数据分成100w一块，共100块。
B. 对每块进行快速排序，分成两堆，如果大堆大于1w个，则对大堆再次进行快速排序，直到小于等于1w停止
（假设此时大堆有N个），此时对小堆进行排序，取最大的10000-N个，这样就找到了这100w中最大的1w个。
C. 100块，每块选出最大的1w，再对这100w使用同样的方法，找出最大的1w个
2. Bit-Map
适用范围：可进行数据的快速查找，判重，删除，一般来说数据范围是int的10倍以下
解法：用一个例子来说明吧，这样直观一点。
假设对7, 6, 3, 5这四个数进行排序，首先初始化一个byte，8位，可表示为0 0 0 0 0 0 0 0
对于7，将第七位置1，对剩下几个数执行同样操作，则最后该byte变为 0 0 1 0 1 1 1 0
最后一步，遍历，将置1位的序号逐个输出，即3，5， 6，7
3. 红黑树
解法：用一个红黑树维护这1w个数，然后遍历其他数字，来替换红黑树中最小的数（这是在网上看到的算法，
我感觉用赢 者树也是可以的）
如果数据中有重复，则对于Bit-Map，找出前1w个数，对这1w个数建立Hash Table，然后再次遍历这一亿个数，同时对Hash Table中的数字 计数，最后根据计数找出前1w个（包含重复）
直接上：
- hash映射：顺序读取10个文件，按照hash(query)%10的结果将query写入到另外10个文件（记为）中。这样新生成的文件每个的大小大约也1G（假设hash函数是随机的）。
- hash统计：找一台内存在2G左右的机器，依次对用hash_map(query, query_count)来统计每个query出现的次数。注：hash_map(query,query_count)是用来统计每个query的出现次数，不是存储他们的值，出现一次，则count+1。
- 堆/快速/归并排序：利用快速/堆/归并排序按照出现次数进行排序。将排序好的query和对应的query_cout输出到文件中。这样得到了10个排好序的文件（记为）。对这10个文件进行归并排序（内排序与外排序相结合）。
方案2：一般query的总量是有限的，只是重复的次数比较多而已，可能对于所有的query，一次性就可以加入到内存了。这样，我们就可以采用trie树/hash_map等直接来统计每个query出现的次数，然后按出现次数做快速/堆/归并排序就可以了。
方案3：与方案1类似，但在做完hash，分成多个文件后，可以交给多个文件来处理，采用分布式的架构来处理（比如MapReduce），最后再进行合并。
方案1：可以估计每个文件安的大小为50G×64=320G，远远大于内存限制的4G。所以不可能将其完全加载到内存中处理。考虑采取分而治之的方法。
- 分而治之/hash映射：遍历文件a，对每个url求取
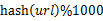，然后根据所取得的值将url分别存储到1000个小文件（记为
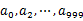,这里漏写个了a1）中。这样每个小文件的大约为300M。 - hash统计：遍历文件b，采取和a相同的方式将url分别存储到1000小文件中（记为
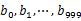）。这样处理后，所有可能相同的url都在对应的小文件（
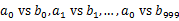）中，不对应的小文件不可能有相同的url。然后我们只要求出1000对小文件中相同的url即可。 - 求每对小文件中相同的url时，可以把其中一个小文件的url存储到hash_set中。然后遍历另一个小文件的每个url，看其是否在刚才构建的hash_set中，如果是，那么就是共同的url，存到文件里面就可以了。
方案2：如果允许有一定的错误率，可以使用Bloom filter，4G内存大概可以表示340亿bit。将其中一个文件中的url使用Bloom filter映射为这340亿bit，然后挨个读取另外一个文件的url，检查是否与Bloom filter，如果是，那么该url应该是共同的url（注意会有一定的错误率）。
9、怎么在海量数据中找出重复次数最多的一个？
方案1：先做hash，然后求模映射为小文件，求出每个小文件中重复次数最多的一个，并记录重复次数。然后找出上一步求出的数据中重复次数最多的一个就是所求（具体参考前面的题）。
10、上千万或上亿数据（有重复），统计其中出现次数最多的钱N个数据。
方案1：上千万或上亿的数据，现在的机器的内存应该能存下。所以考虑采用hash_map/搜索二叉树/红黑树等来进行统计次数。然后就是取出前N个出现次数最多的数据了，可以用第2题提到的堆机制完成。
11、 1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。请怎么设计和实现？
- 方案1：这题用trie树比较合适，hash_map也行。
首先映射为内存可以处理的n个小文件，这时相同的字符串肯定在同一个文件中，在每个小文件中使用hash_set取出重复的字符串，之后写 到一个文件中，依次处理n个文件，即可得到结果。。
- 方案2：from xjbzju:，1000w的数据规模插入操作完全不现实，以前试过在stl下100w元素插入set中已经慢得不能忍受，觉得基于hash的实现不会比红黑树好太多，使用vector+sort+unique都要可行许多，建议还是先hash成小文件分开处理再综合。
- 1、hash_set在千万级数据下，insert操作优于set? 这位blog：http://t.cn/zOibP7t 给的实践数据可靠不?
- 2、那map和hash_map的性能比较呢? 谁做过相关实验?
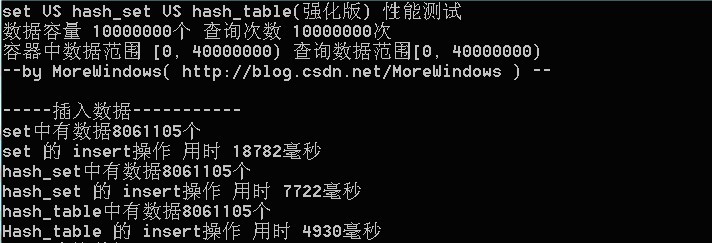
- 3、那查询操作呢，如下段文字所述?
或者小数据量时用map，构造快，大数据量时用hash_map?
rbtree PK hashtable
据朋友№邦卡猫№的做的红黑树和hash table的性能测试中发现：当数据量基本上int型key时，hash table是rbtree的3-4倍，但hash table一般会浪费大概一半内存。
因为hash table所做的运算就是个%，而rbtree要比较很多，比如rbtree要看value的数据 ，每个节点要多出3个指针（或者偏移量） 如果需要其他功能，比如，统计某个范围内的key的数量，就需要加一个计数成员。
OK，更多请待后续实验论证。接下来，咱们来看第二种方法，双层捅划分。
密匙二、双层桶划分
双层桶划分----其实本质上还是分而治之的思想，重在“分”的技巧上！
适用范围：第k大，中位数，不重复或重复的数字
基本原理及要点：因为元素范围很大，不能利用直接寻址表，所以通过多次划分，逐步确定范围，然后最后在一个可以接受的范围内进行。可以通过多次缩小，双层只是一个例子。
扩展：
问题实例：
11、2.5亿个整数中找出不重复的整数的个数，内存空间不足以容纳这2.5亿个整数。
有点像鸽巢原理，整数个数为2^32,也就是，我们可以将这2^32个数，划分为2^8个区域(比如用单个文件代表一个区域)，然后将数据分离到不同的区域，然后不同的区域在利用bitmap就可以直接解决了。也就是说只要有足够的磁盘空间，就可以很方便的解决。
#include<stdio.h>
#include<memory.h>
//用char数组存储2-Bitmap,不用考虑大小端内存的问题
unsigned char flags[1000]; //数组大小自定义
unsigned get_val(int idx)
{
int i = idx/4;
int j = idx%4;
unsigned ret = (flags[i]&(0x3<<(2*j)))>>(2*j);
return ret;
}
unsigned set_val(int idx, unsigned int val)
{
int i = idx/4;
int j = idx%4;
unsigned tmp = (flags[i]&~((0x3<<(2*j))&0xff)) | (((val%4)<<(2*j))&0xff);
flags[i] = tmp;
return 0;
}
unsigned add_one(int idx)
{
if (get_val(idx)>=2) {
return 1;
}
else {
set_val(idx, get_val(idx)+1);
return 0;
}
}
//只测试非负数的情况;
//假如考虑负数的话,需增加一个2-Bitmap数组.
int a[]={1, 3, 5, 7, 9, 1, 3, 5, 7, 1, 3, 5,1, 3, 1,10,2,4,6,8,0};
int main()
{
int i;
memset(flags, 0, sizeof(flags));
printf("原数组为:");
for(i=0;i < sizeof(a)/sizeof(int); ++i) {
printf("%d ", a[i]);
add_one(a[i]);
}
printf("\r\n");
printf("只出现过一次的数:");
for(i=0;i < 100; ++i) {
if(get_val(i) == 1)
printf("%d ", i);
}
printf("\r\n");
return 0;
}
除了用2-Bitmap来计数标记以外,也可以用两个1-Bitmap来实现(如果考虑正负数的情况,就四个1-Bitmap)
12、5亿个int找它们的中位数。
- 思路一：这个例子比上面那个更明显。首先我们将int划分为2^16个区域，然后读取数据统计落到各个区域里的数的个数，之后我们根据统计结果就可以判断中位数落到那个区域，同时知道这个区域中的第几大数刚好是中位数。然后第二次扫描我们只统计落在这个区域中的那些数就可以了。
实际上，如果不是int是int64，我们可以经过3次这样的划分即可降低到可以接受的程度。即可以先将int64分成2^24个区域，然后确定区域的第几大数，在将该区域分成2^20个子区域，然后确定是子区域的第几大数，然后子区域里的数的个数只有2^20，就可以直接利用direct addr table进行统计了。 - 思路二@绿色夹克衫：同样需要做两遍统计，如果数据存在硬盘上，就需要读取2次。
方法同基数排序有些像，开一个大小为65536的Int数组，第一遍读取，统计Int32的高16位的情况，也就是0-65535，都算作0,65536 - 131071都算作1。就相当于用该数除以65536。Int32 除以 65536的结果不会超过65536种情况，因此开一个长度为65536的数组计数就可以。每读取一个数，数组中对应的计数+1，考虑有负数的情况，需要将结果加32768后，记录在相应的数组内。
第一遍统计之后，遍历数组，逐个累加统计，看中位数处于哪个区间，比如处于区间k，那么0- k-1的区间里数字的数量sum应该<n/2（2.5亿）。而k+1 - 65535的计数和也<n/2，第二遍统计同上面的方法类似，但这次只统计处于区间k的情况，也就是说(x / 65536) + 32768 = k。统计只统计低16位的情况。并且利用刚才统计的sum，比如sum = 2.49亿，那么现在就是要在低16位里面找100万个数(2.5亿-2.49亿)。这次计数之后，再统计一下，看中位数所处的区间，最后将高位和低位组合一下就是结果了。
密匙三：Bloom filter/Bitmap
Bloom filter
关于什么是Bloom filter，请参看blog内此文：
适用范围：可以用来实现数据字典，进行数据的判重，或者集合求交集
基本原理及要点：
对于原理来说很简单，位数组+k个独立hash函数。将hash函数对应的值的位数组置1，查找时如果发现所有hash函数对应位都是1说明存在，很明显这个过程并不保证查找的结果是100%正确的。同时也不支持删除一个已经插入的关键字，因为该关键字对应的位会牵动到其他的关键字。所以一个简单的改进就是 counting Bloom filter，用一个counter数组代替位数组，就可以支持删除了。
还有一个比较重要的问题，如何根据输入元素个数n，确定位数组m的大小及hash函数个数。当hash函数个数k=(ln2)*(m/n)时错误率最小。在错误率不大于E的情况下，m至少要等于n*lg(1/E)才能表示任意n个元素的集合。但m还应该更大些，因为还要保证bit数组里至少一半为0，则m应该>=nlg(1/E)*lge 大概就是nlg(1/E)1.44倍(lg表示以2为底的对数)。
举个例子我们假设错误率为0.01，则此时m应大概是n的13倍。这样k大概是8个。
注意这里m与n的单位不同，m是bit为单位，而n则是以元素个数为单位(准确的说是不同元素的个数)。通常单个元素的长度都是有很多bit的。所以使用bloom filter内存上通常都是节省的。
扩展：
Bloom filter将集合中的元素映射到位数组中，用k（k为哈希函数个数）个映射位是否全1表示元素在不在这个集合中。Counting bloom filter（CBF）将位数组中的每一位扩展为一个counter，从而支持了元素的删除操作。Spectral Bloom Filter（SBF）将其与集合元素的出现次数关联。SBF采用counter中的最小值来近似表示元素的出现频率。
13、给你A,B两个文件，各存放50亿条URL，每条URL占用64字节，内存限制是4G，让你找出A,B文件共同的URL。如果是三个乃至n个文件呢？
根据这个问题我们来计算下内存的占用，4G=2^32大概是40亿*8大概是340亿，n=50亿，如果按出错率0.01算需要的大概是650亿个bit。现在可用的是340亿，相差并不多，这样可能会使出错率上升些。另外如果这些urlip是一一对应的，就可以转换成ip，则大大简单了。
同时，上文的第5题：给定a、b两个文件，各存放50亿个url，每个url各占64字节，内存限制是4G，让你找出a、b文件共同的url？如果允许有一定的错误率，可以使用Bloom filter，4G内存大概可以表示340亿bit。将其中一个文件中的url使用Bloom filter映射为这340亿bit，然后挨个读取另外一个文件的url，检查是否与Bloom filter，如果是，那么该url应该是共同的url（注意会有一定的错误率）。
Bitmap
- 关于什么是Bitmap，请看blog内此文第二部分：http://blog.csdn.net/v_july_v/article/details/6685962。
下面关于Bitmap的应用，直接上题，如下第9、10道：
14/11题、在2.5亿个整数中找出不重复的整数，注，内存不足以容纳这2.5亿个整数。
方案1：采用2-Bitmap（每个数分配2bit，00表示不存在，01表示出现一次，10表示多次，11无意义）进行，共需内存2^32 * 2 bit=1 GB内存，还可以接受。然后扫描这2.5亿个整数，查看Bitmap中相对应位，如果是00变01，01变10，10保持不变。所描完事后，查看bitmap，把对应位是01的整数输出即可。
方案2：也可采用与第1题类似的方法，进行划分小文件的方法。然后在小文件中找出不重复的整数，并排序。然后再进行归并，注意去除重复的元素。
15、腾讯面试题：给40亿个不重复的unsigned int的整数，没排过序的，然后再给一个数，如何快速判断这个数是否在那40亿个数当中？
第一反应时快速排序+二分查找。以下是其它更好的方法：
方案1：frome oo，用位图/Bitmap的方法，申请512M的内存，一个bit位代表一个unsigned int值。读入40亿个数，设置相应的bit位，读入要查询的数，查看相应bit位是否为1，为1表示存在，为0表示不存在。
方案2：这个问题在《编程珠玑》里有很好的描述，大家可以参考下面的思路，探讨一下：
又因为2^32为40亿多，所以给定一个数可能在，也可能不在其中；
这里我们把40亿个数中的每一个用32位的二进制来表示
假设这40亿个数开始放在一个文件中。
然后将这40亿个数分成两类:
1.最高位为0
2.最高位为1
并将这两类分别写入到两个文件中，其中一个文件中数的个数<=20亿，而另一个>=20亿（这相当于折半了）；
与要查找的数的最高位比较并接着进入相应的文件再查找
再然后把这个文件为又分成两类:
1.次最高位为0
2.次最高位为1
并将这两类分别写入到两个文件中，其中一个文件中数的个数<=10亿，而另一个>=10亿（这相当于折半了）；
与要查找的数的次最高位比较并接着进入相应的文件再查找。
…….
以此类推，就可以找到了,而且时间复杂度为O(logn)，方案2完。
16、给40亿个unsigned int的整数，如何判断这40亿个数中哪些数重复？
同理，可以申请512M的内存空间，然后读取40亿个整数，并且将相应的bit位置1。如果是第一次读取某个数据，则在将该bit位置1之前，此bit位必定是0；如果是第二次读取该数据，则可根据相应的bit位是否为1判断该数据是否重复。
附：这里，再简单介绍下，位图方法：
使用位图法判断整形数组是否存在重复
判断集合中存在重复是常见编程任务之一，当集合中数据量比较大时我们通常希望少进行几次扫描，这时双重循环法就不可取了。
位图法比较适合于这种情况，它的做法是按照集合中最大元素max创建一个长度为max+1的新数组，然后再次扫描原数组，遇到几就给新数组的第几位置上 1，如遇到5就给新数组的第六个元素置1，这样下次再遇到5想置位时发现新数组的第六个元素已经是1了，这说明这次的数据肯定和以前的数据存在着重复。这 种给新数组初始化时置零其后置一的做法类似于位图的处理方法故称位图法。它的运算次数最坏的情况为2N。如果已知数组的最大值即能事先给新数组定长的话效 率还能提高一倍。
密匙四、Trie树/数据库/倒排索引
Trie树
适用范围：数据量大，重复多，但是数据种类小可以放入内存
基本原理及要点：实现方式，节点孩子的表示方式
扩展：压缩实现。
问题实例：
- 上面的第2题：寻找热门查询：查询串的重复度比较高，虽然总数是1千万，但如果除去重复后，不超过3百万个，每个不超过255字节。
- 上面的第5题：有10个文件，每个文件1G，每个文件的每一行都存放的是用户的query，每个文件的query都可能重复。要你按照query的频度排序。
- 1000万字符串，其中有些是相同的(重复),需要把重复的全部去掉，保留没有重复的字符串。请问怎么设计和实现？
- 上面的第8题：一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词。其解决方法是：用trie树统计每个词出现的次数，时间复杂度是O(n*le)（le表示单词的平准长度），然后是找出出现最频繁的前10个词。
更多有关Trie树的介绍，请参见此文：从Trie树（字典树）谈到后缀树。
数据库索引
适用范围：大数据量的增删改查
基本原理及要点：利用数据的设计实现方法，对海量数据的增删改查进行处理。
- 关于数据库索引及其优化，更多可参见此文：http://www.cnblogs.com/pkuoliver/archive/2011/08/17/mass-data-topic-7-index-and-optimize.html；
- 关于MySQL索引背后的数据结构及算法原理，这里还有一篇很好的文章：http://www.codinglabs.org/html/theory-of-mysql-index.html；
- 关于B 树、B+ 树、B* 树及R 树，本blog内有篇绝佳文章：http://blog.csdn.net/v_JULY_v/article/details/6530142。
倒排索引(Inverted index)
适用范围：搜索引擎，关键字查询
基本原理及要点：为何叫倒排索引？一种索引方法，被用来存储在全文搜索下某个单词在一个文档或者一组文档中的存储位置的映射。
以英文为例，下面是要被索引的文本：
T0 = "it is what it is"
T1 = "what is it"
T2 = "it is a banana"
我们就能得到下面的反向文件索引：
"a": {2}
"banana": {2}
"is": {0, 1, 2}
"it": {0, 1, 2}
"what": {0, 1}
检索的条件"what","is"和"it"将对应集合的交集。
正向索引开发出来用来存储每个文档的单词的列表。正向索引的查询往往满足每个文档有序频繁的全文查询和每个单词在校验文档中的验证这样的查询。在正向索引中，文档占据了中心的位置，每个文档指向了一个它所包含的索引项的序列。也就是说文档指向了它包含的那些单词，而反向索引则是单词指向了包含它的文档，很容易看到这个反向的关系。
扩展：
问题实例：文档检索系统，查询那些文件包含了某单词，比如常见的学术论文的关键字搜索。
关于倒排索引的应用，更多请参见：
密匙五、外排序
适用范围：大数据的排序，去重
基本原理及要点：外排序的归并方法，置换选择败者树原理，最优归并树
扩展：
问题实例：
1).有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16个字节，内存限制大小是1M。返回频数最高的100个词。
这个数据具有很明显的特点，词的大小为16个字节，但是内存只有1M做hash明显不够，所以可以用来排序。内存可以当输入缓冲区使用。
关于多路归并算法及外排序的具体应用场景，请参见blog内此文：
密匙六、分布式处理之Mapreduce
MapReduce是一种计算模型，简单的说就是将大批量的工作（数据）分解（MAP）执行，然后再将结果合并成最终结果（REDUCE）。这样做的好处是可以在任务被分解后，可以通过大量机器进行并行计算，减少整个操作的时间。但如果你要我再通俗点介绍，那么，说白了，Mapreduce的原理就是一个归并排序。
适用范围：数据量大，但是数据种类小可以放入内存
基本原理及要点：将数据交给不同的机器去处理，数据划分，结果归约。
扩展：
问题实例：
- The canonical example application of MapReduce is a process to count the appearances of each different word in a set of documents:
- 海量数据分布在100台电脑中，想个办法高效统计出这批数据的TOP10。
- 一共有N个机器，每个机器上有N个数。每个机器最多存O(N)个数并对它们操作。如何找到N^2个数的中数(median)？
更多具体阐述请参见blog内：
其它模式/方法论，结合操作系统知识
- 物理地址 (physical address): 放在寻址总线上的地址。放在寻址总线上，如果是读，电路根据这个地址每位的值就将相应地址的物理内存中的数据放到数据总线中传输。如果是写，电路根据这个 地址每位的值就将相应地址的物理内存中放入数据总线上的内容。物理内存是以字节(8位)为单位编址的。
- 虚拟地址 (virtual address): 4G虚拟地址空间中的地址，程序中使用的都是虚拟地址。 使用了分页机制之后，4G的地址空间被分成了固定大小的页，每一页或者被映射到物理内存，或者被映射到硬盘上的交换文件中，或者没有映射任何东西。对于一 般程序来说，4G的地址空间，只有一小部分映射了物理内存，大片大片的部分是没有映射任何东西。物理内存也被分页，来映射地址空间。对于32bit的 Win2k，页的大小是4K字节。CPU用来把虚拟地址转换成物理地址的信息存放在叫做页目录和页表的结构里。
操作系统中的方法，先生成4G的地址表，在把这个表划分为小的4M的小文件做个索引，二级索引。30位前十位表示第几个4M文件，后20位表示在这个4M文件的第几个，等等，基于key value来设计存储，用key来建索引。
但如果现在只有10000个数，然后怎么去随机从这一万个数里面随机取100个数？请读者思考。更多海里数据处理面试题，请参见此文第一部分：http://blog.csdn.net/v_july_v/article/details/6685962。
