前记
博主距离上次正式发 blog 已经过 114514 年了。进入大学后关于 OI 方面接触就少了。OI 的姿势越来越不会,导致我 NOI2022 题解鸽到现在。
关于为什么想发这篇 blog,更多的还是对这方面的了解甚少,想通过写写文的方式寻找与其相关的灵感。
学习这套理论,源自其中的一个 project 的 AI 设计(任何算法,哪怕暴力都可)。博主想把握好这个机会学习些关于现代搜索和 AI 方面的理论,当然,人工神经网络只是辅助该 AI 实现的一个工具。
本文大多是一些摘记,从多处拼接而来,可能存在不严谨的地方,毕竟是无师自学,寻找相关资料已是不易之事。如有错误之处,望能不吝赐教。
1.模型
根据名称,不难得知人工神经网络源于生物学的神经网络。人的大脑由众多神经元组成,单个神经元的模式图如下:
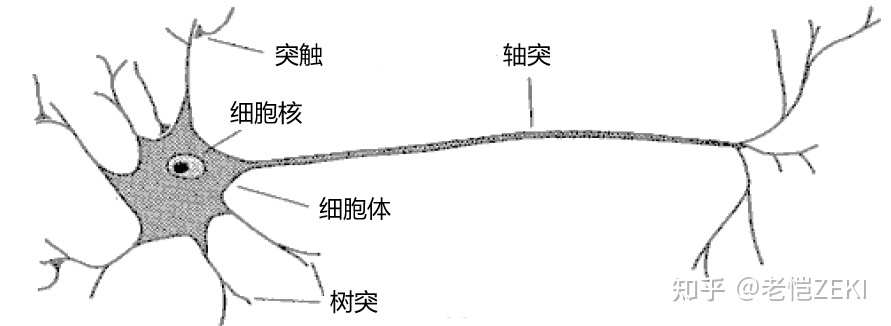
根据生物学研究,树突和轴突大致可以理解成对该神经元的输入和输出,于是计算机科学家对其进行简化,将神经元看成一个节点,又叫 单一神经元,于是得到:

其中 \(x\) 称为 输入,\(w\) 被称为 权重,\(b\) 成为 偏移项,作用是对其进行一次水平的调整。\(z\) 是一个运算中间值,\(o\) 是将 \(z\) 通过一个 激活函数 \(f\) 得到,称为 输出值。简单来说,公式为 \(o=f(z)=f(wx+b)\)。
如果 \(\boldsymbol x\in\R^{n\times 1}\),相应地,\(\boldsymbol w\in\R^{n\times 1}\),那么得到 \(o=f(\boldsymbol w^T\boldsymbol x+b)\)。
下面来说说激活函数 \(f\)。常见的有以下几类:
- Sigmoid \(\sigma\):取值 0 到 1,表达式为 \(f(x)=\frac1{1+e^{-x}}\),以及 \(f'(x)=f(x)(1-f(x))\);
- 正切函数 Tanh:\(f(x)=\tanh x\)。取值 -1 到 +1 ,平均值为 0,当 \(x\rightarrow 0\) 时,\(f'(x)\rightarrow 1\);
- 高斯函数:\(f(x)=\exp(-\frac{x^2}{\sigma^2})\);
- ReLU 函数:\(f(x)=\max\{0,x\}\)。听说很强大,能避免幂运算和梯度消失。
2.BPNN(反向传播神经网络)
多个神经元形成多层,且每层若干神经元,它们相互交叉连接,就能构成神经网络。前一层神经元作为后一层的输入,最后一层直接给出整个网络的输出,称为 输出层,输出层之前的层称为 隐含层。当一个神经网络有一层以上的隐藏层,称其为深度学习网络。定义神经元的层数为隐含层数 + 输出层。

假设输入层是一个 \(n\) 维向量,记成 \(\boldsymbol x\),输出层为 \(m\) 维向量,记成 \(\boldsymbol y\),假设一个三层神经网络,各层的 权重矩阵、偏移向量、入参向量 和 出参向量 分别为:
\[\boldsymbol w^{(i)}=
\left[
\begin{matrix}
w_{11}^{(i)}&w_{12}^{(i)}&\cdots&w_{1n}^{(i)}\\
w_{21}^{(i)}&w_{22}^{(i)}&\cdots&w_{2n}^{(i)}\\
\vdots&\vdots&\ddots&\vdots\\
w_{m1}^{(i)}&w_{m2}^{(i)}&\cdots&w_{mn}^{(i)}\\
\end{matrix}
\right]
\]
\[\boldsymbol b^{(i)}=
\left[
\begin{matrix}
b_1^{(i)}\\
b_2^{(i)}\\
\vdots\\
b_m^{(i)}\\
\end{matrix}
\right]
\]
\[\boldsymbol z^{(i)}=
\left[
\begin{matrix}
z_1^{(i)}\\
z_2^{(i)}\\
\vdots\\
z_m^{(i)}\\
\end{matrix}
\right]
\]
\[\boldsymbol o^{(i)}=
\left[
\begin{matrix}
o_1^{(i)}\\
o_2^{(i)}\\
\vdots\\
o_m^{(i)}\\
\end{matrix}
\right]
\]
其中 \(w_{jk}^{(i)}\) 表示第 \(i\) 层神经元第 \(k\) 个输入源传达到第 \(j\) 个神经元的强度权重,\(b^{(i)}_j\) 表示第 \(i\) 层第 \(j\) 个神经元的输入偏移量,\(z_j^{(i)}\) 表示第 \(i\) 层第 \(j\) 个神经元的激活函数入参,\(o_j^{(i)}\) 表示第 \(i\) 层第 \(j\) 个神经元的输出。同时,我们有 \(\boldsymbol y=\boldsymbol o^{(3)}\)。
根据以上定义,我们不难得出运算:
\[\boldsymbol z^{(1)}=\boldsymbol w^{(1)}\boldsymbol x+\boldsymbol b^{(1)},\boldsymbol o^{(1)}=f(\boldsymbol z^{(1)})
\]
\[\boldsymbol z^{(2)}=\boldsymbol w^{(2)}\boldsymbol x+\boldsymbol b^{(2)},\boldsymbol o^{(2)}=f(\boldsymbol z^{(2)})
\]
\[\boldsymbol z^{(3)}=\boldsymbol w^{(3)}\boldsymbol x+\boldsymbol b^{(3)},\boldsymbol o^{(3)}=f(\boldsymbol z^{(3)})
\]
现在我们来讨论训练模型。假设有一种模型,满足若干组要求:对于参数 \(\{\boldsymbol x_1,\cdots,\boldsymbol x_t\}\),以及结果 \(\{\boldsymbol y_1,\cdots,\boldsymbol y_t\}\),我们肯定希望通过该神经网络,能够得到 \(\boldsymbol y_i=\text{BPNN}(\boldsymbol x_i)\),并且随着参数集的推广仍然具有很好的预测作用。事实上,我们很难直接获得如此完美的情况,为了评估训练效果,我们定义 代价函数 \(J=\frac1t\sum\limits_{i=1}^tL_i\),其中 \(L_i\) 表示第 \(i\) 个样本的 训练误差,为了方便计算,定义为 \(\frac12||\boldsymbol y-\boldsymbol y_i||^2\),其中 \(\boldsymbol y\) 表示 \(\text{BPNN}\) 给的输出值。
训练的目的是最小化 \(J\),也就是要找到 \(J\) 的梯度 \(\nabla J\),即 \(\frac1t\sum\limits_{i=1}^t\nabla L_i\)。所以我们来讨论 \(\nabla L\)。
我们来寻找 \(\boldsymbol w\)、\(\boldsymbol b\) 和 \(L\) 的关系,也就是求 偏导 \(\dfrac{\partial L}{\partial\boldsymbol w}\) 和 \(\dfrac{\partial L}{\partial\boldsymbol b}\)。我们仍然假设其为 3 层神经网络,不妨先来看看 \(\boldsymbol w^{(1)}\)。
\[\frac{\partial L}{\partial\boldsymbol w^{(1)}}=
\left[
\begin{matrix}
\frac{\partial L}{\partial w_{11}^{(1)}}&\frac{\partial L}{\partial w_{12}^{(1)}}&\cdots&\frac{\partial L}{\partial w_{1n}^{(1)}}\\
\frac{\partial L}{\partial w_{21}^{(1)}}&\frac{\partial L}{\partial w_{22}^{(1)}}&\cdots&\frac{\partial L}{\partial w_{2n}^{(1)}}\\
\vdots&\vdots&\ddots&\vdots\\
\frac{\partial L}{\partial w_{m1}^{(1)}}&\frac{\partial L}{\partial w_{m2}^{(1)}}&\cdots&\frac{\partial L}{\partial w_{mn}^{(1)}}\\
\end{matrix}
\right]
\]
下面考察 \(\dfrac{\partial L}{\partial w_{ij}^{(1)}}\)。
\[\frac{\partial L}{\partial w_{ij}^{(1)}}=\frac{\partial L}{\partial z_i^{(1)}}\frac{\partial z_i^{(1)}}{\partial w_{ij}^{(1)}}=\frac{\partial L}{\partial z_i^{(1)}}x_j
\]
所以得到
\[\frac{\partial L}{\partial\boldsymbol w^{(1)}}=
\left[
\begin{matrix}
\frac{\partial L}{\partial z_1^{(1)}}\\
\frac{\partial L}{\partial z_2^{(1)}}\\
\vdots\\
\frac{\partial L}{\partial z_m^{(1)}}\\
\end{matrix}
\right]
\times
\boldsymbol x^T
\]
我们把右式左边的列向量记为 \(\boldsymbol\delta^{(1)}\),那么:
\[\frac{\partial L}{\partial\boldsymbol w^{(1)}}=\boldsymbol\delta^{(1)}\boldsymbol x^T
\]
同理:
\[\frac{\partial L}{\partial\boldsymbol w^{(2)}}=\boldsymbol\delta^{(2)}\left(\boldsymbol o^{(1)}\right)^T
\]
\[\frac{\partial L}{\partial\boldsymbol w^{(3)}}=\boldsymbol\delta^{(3)}\left(\boldsymbol o^{(2)}\right)^T
\]
再来考察 \(\boldsymbol b^{(1)}\)。
\[\frac{\partial L}{\partial\boldsymbol b^{(1)}}=
\left[
\begin{matrix}
\frac{\partial L}{\partial b_1^{(1)}}\\
\frac{\partial L}{\partial b_2^{(1)}}\\
\vdots\\
\frac{\partial L}{\partial b_m^{(1)}}\\
\end{matrix}
\right]
\]
同样地:
\[\frac{\partial L}{\partial b_i^{(1)}}=\frac{\partial L}{\partial z_i^{(1)}}\frac{\partial z_i^{(1)}}{\partial b_i^{(1)}}=\frac{\partial L}{\partial z_i^{(1)}}
\]
所以得到:
\[\frac{\partial L}{\partial\boldsymbol b^{(1)}}=
\left[
\begin{matrix}
\frac{\partial L}{\partial z_1^{(1)}}\\
\frac{\partial L}{\partial z_2^{(1)}}\\
\vdots\\
\frac{\partial L}{\partial z_m^{(1)}}\\
\end{matrix}
\right]
=\boldsymbol\delta^{(1)}
\]
同理
\[\frac{\partial L}{\partial\boldsymbol b^{(2)}}=\boldsymbol\delta^{(2)}
\]
\[\frac{\partial L}{\partial\boldsymbol b^{(3)}}=\boldsymbol\delta^{(3)}
\]
对于训练样本 \(L\leftarrow\{\boldsymbol w_1,\boldsymbol w_2,\boldsymbol w_3,\boldsymbol b_1,\boldsymbol b_2,\boldsymbol b_3\}\),得到 \(\nabla L\leftarrow\{\boldsymbol\delta^{(1)}\boldsymbol x^T,\boldsymbol\delta^{(2)}\left(\boldsymbol o^{(1)}\right)^T,\boldsymbol\delta^{(3)}\left(\boldsymbol o^{(2)}\right)^T,\boldsymbol\delta^{(1)},\boldsymbol\delta^{(2)},\boldsymbol\delta^{(3)}\}\)。
最后一点,如何求 \(\boldsymbol\delta\)?我们先来看 \(\boldsymbol\delta^{(1)}\),注意到
\[\frac{\partial L}{\partial z_i^{(1)}}=\frac{\partial L}{\partial o_i^{(1)}}\frac{\partial o_i^{(1)}}{\partial z_i^{(1)}}=f'(z_i^{(1)})\frac{\partial L}{\partial o_i^{(1)}}=f'(z_i^{(1)})\sum_{j=1}^m\frac{\partial L}{\partial z_j^{(2)}}\frac{\partial z_j^{(2)}}{\partial o_i^{(1)}}=f'(z_i^{(1)})\sum_{j=1}^m\frac{\partial L}{\partial z_j^{(2)}}w_{ji}^{(2)}
\]
所以有:
\[\frac{\partial L}{\partial z_i^{(1)}}=f'(z_i^{(1)})
\left[
\begin{matrix}
w_{1i}^{(2)}&w_{2i}^{(2)}&\cdots&w_{m'i}^{(2)}
\end{matrix}
\right]
\left[
\begin{matrix}
\frac{\partial L}{\partial z_1^{(2)}}\\
\frac{\partial L}{\partial z_2^{(2)}}\\
\vdots\\
\frac{\partial L}{\partial z_{m'}^{(2)}}
\end{matrix}
\right]
\]
\[\boldsymbol\delta^{(1)}=
\left[
\begin{matrix}
\frac{\partial L}{\partial z_1^{(1)}}\\
\frac{\partial L}{\partial z_2^{(1)}}\\
\vdots\\
\frac{\partial L}{\partial z_m^{(1)}}\\
\end{matrix}
\right]=
\left[
\begin{matrix}
f'(z_1^{(1)})&&&\\
&f'(z_2^{(1)})&&\\
&&\ddots&\\
&&&f'(z_m^{(1)})\\
\end{matrix}
\right]
\left[
\begin{matrix}
w_{11}^{(2)}&w_{21}^{(2)}&\cdots&w_{m'1}^{(2)}\\
w_{12}^{(2)}&w_{22}^{(2)}&\cdots&w_{m'2}^{(2)}\\
\vdots&\vdots&\ddots&\vdots\\
w_{1m}^{(2)}&w_{2m}^{(2)}&\cdots&w_{m'm}^{(2)}
\end{matrix}
\right]
\left[
\begin{matrix}
\frac{\partial L}{\partial z_1^{(2)}}\\
\frac{\partial L}{\partial z_2^{(2)}}\\
\vdots\\
\frac{\partial L}{\partial z_{m'}^{(2)}}
\end{matrix}
\right]
\]
简单来写就是:\(\boldsymbol\delta^{(1)}=\text{Diag}\left(f'(\boldsymbol z^{(1)})\right)\left(\boldsymbol w^{(2)}\right)^T\boldsymbol\delta^{(2)}\);同样地,\(\boldsymbol\delta^{(2)}=\text{Diag}\left(f'(\boldsymbol z^{(2)})\right)\left(\boldsymbol w^{(3)}\right)^T\boldsymbol\delta^{(3)}\)。当然,边界 \(\boldsymbol\delta^{(3)}\) 是要单独考虑的。
考虑 \(\dfrac{\partial L}{\partial z_i^{(3)}}\):
\[\dfrac{\partial L}{\partial z_i^{(3)}}=\dfrac{\partial L}{\partial o_i^{(3)}}\dfrac{\partial o_i^{(3)}}{\partial z_i^{(3)}}=f'(z_i^{(3)})\dfrac{\partial L}{\partial y_i}=f'(z_i^{(3)})\dfrac{\partial\left(\dfrac12||\boldsymbol y-\boldsymbol{\hat y}||^2\right)}{\partial y_i}=f'(z_i^{(3)})(y_i-\hat{y_i})
\]
所以得到
\[\boldsymbol\delta^{(3)}=
\left[
\begin{matrix}
\frac{\partial L}{\partial z_1^{(3)}}\\
\frac{\partial L}{\partial z_2^{(3)}}\\
\vdots\\
\frac{\partial L}{\partial z_m^{(3)}}\\
\end{matrix}
\right]=
\text{Diag}\left(f'(\boldsymbol z^{(3)})\right)(\boldsymbol y-\boldsymbol{\hat y})
\]
至此,推导结束。
将所有的 \(\nabla L\) 求加权平均,选取一个合适的调整系数 \(\lambda\),根据梯度反向调整即可(这样 \(J\rightarrow 0\))。也就是 梯度下降。
训练的时候,有三种梯度下降的方法:
批量梯度下降(Batch Gradient Descent,BGD):即每次训练迭代时,使用当前训练样本集合的全集来计算代价函数梯度。
随机梯度下降(Stochastic Gradient Descent,SGD):即每次训练迭代时,仅使用当前训练样本集合中的一个随机样本来计算代价函数梯度。
小批量梯度下降(Mini-Batch Gradient Descent, MBGD):即每次训练迭代时,使用当前训练样本集合中的一个随机子集样本来计算代价函数梯度。此训练方案是上述两种方案的折中,一般效果最好。
3.GRNN
有空再学(未完待续)





 浙公网安备 33010602011771号
浙公网安备 33010602011771号