[NOI2020]超现实树
超现实树(Surreal)
时隔 10 个月,我又来复盘此题啦 /se
当时蒟蒻不会这道题,胡了个三树合并的做法,以为 GG 但发现竟然还有 40 pts /jy
什么是三棵树合并?一个简单的例子:
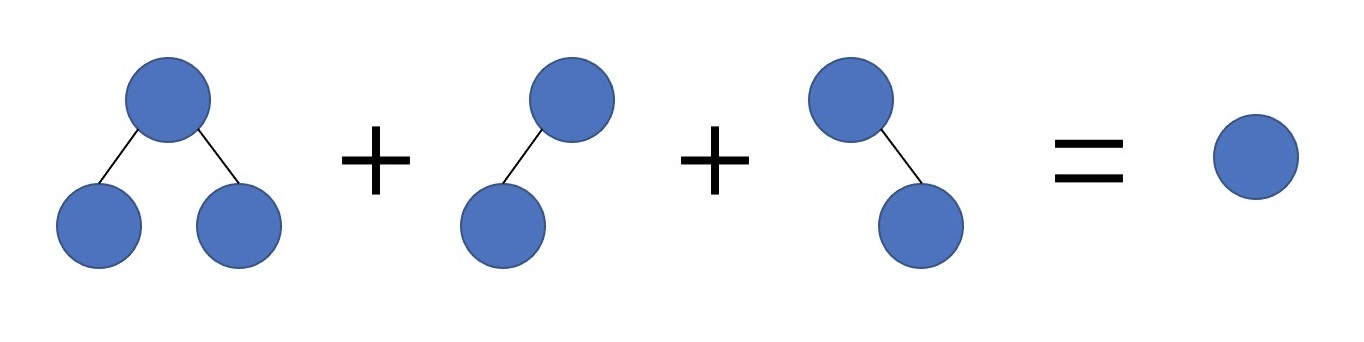
这是第 2 组样例。它的答案为 Almost Complete。对于更复杂的树,如果其它部分完全一样,三棵树分别是如上的结构,那么可以合并到一块,例如
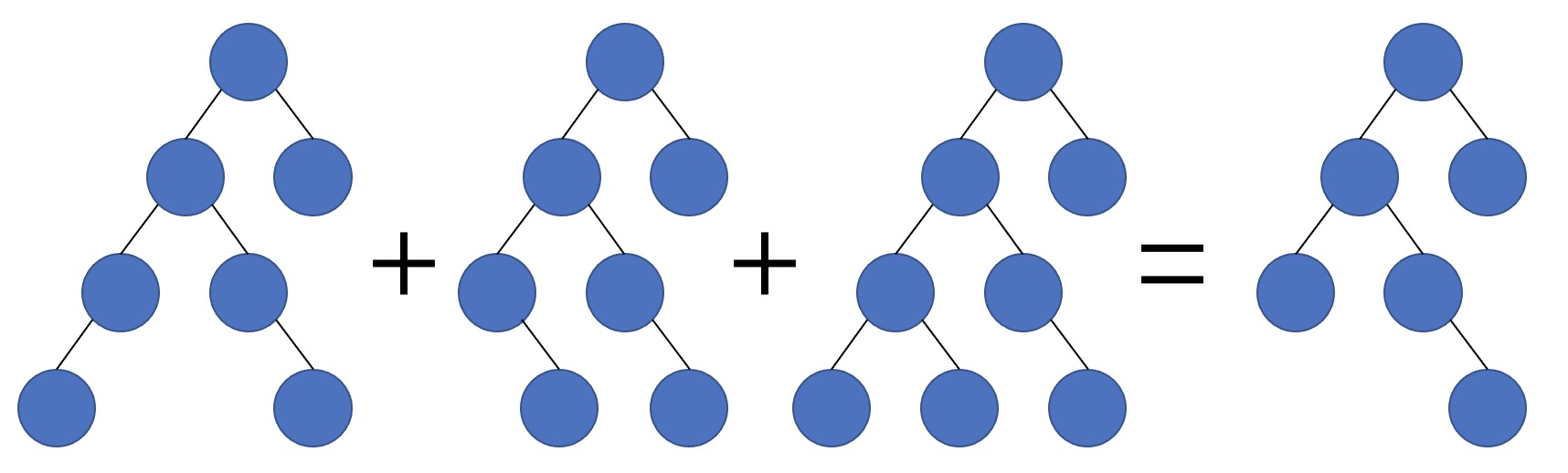
如果能合并成像右边一样是一个只包含根节点的树,它就是 Almost Complete,否则就是 No。
于是你开始信心满满地开始 rush 一份线性的带 Hash 的代码,当你开始一组组地跑样例时,发现 Case 5 WA 了!
如果出题人按照开始只下发前 4 组样例,估计大多数错解选手就会跑路看 T1 或 T3,还好他是 Almost 良心 的(bushi),补发了两组!
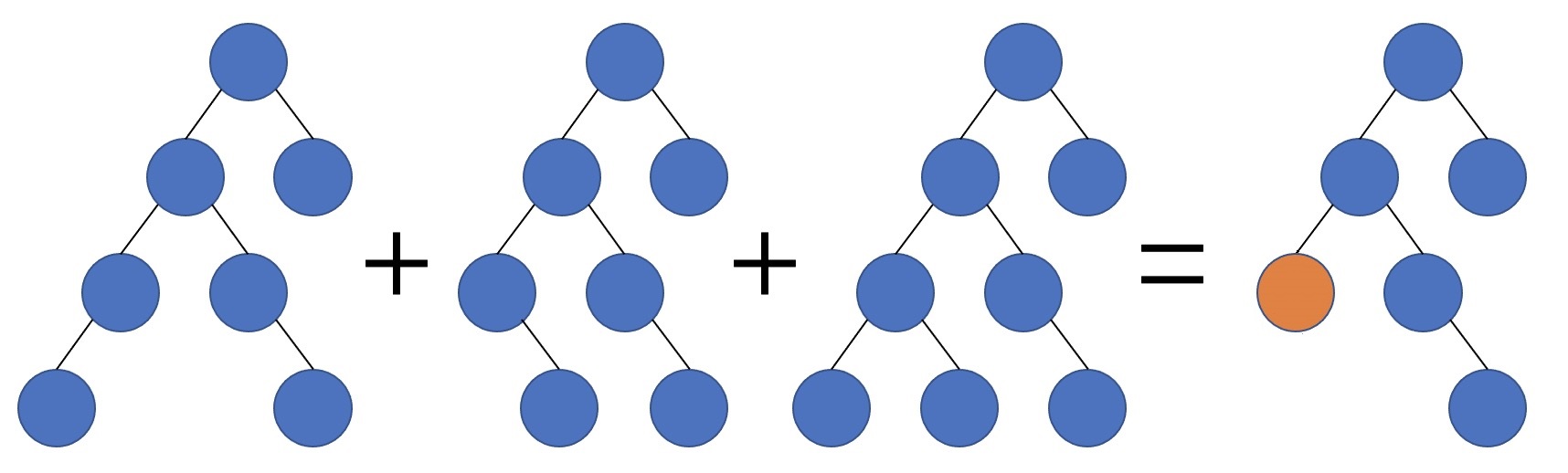
此时要反思为什么上面是错的。在第一幅图中:
\({\rm grow}(\)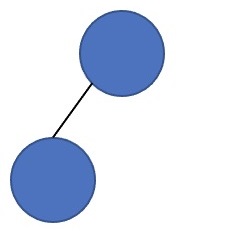 \()+{\rm grow}(\)
\()+{\rm grow}(\)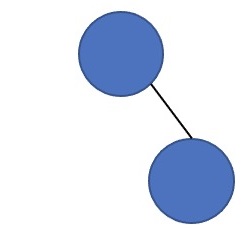 \()+{\rm grow}(\)
\()+{\rm grow}(\)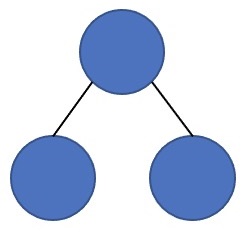 \()={\rm grow}(\)
\()={\rm grow}(\) \()\setminus\{\)
\()\setminus\{\) \(\}\ne{\rm grow}(\)
\(\}\ne{\rm grow}(\) \()\)
\()\)
发现两者不完全等价!我们尝试修正该方法。我们使用红色的节点来 特殊化 被合并的节点,也就是像这样

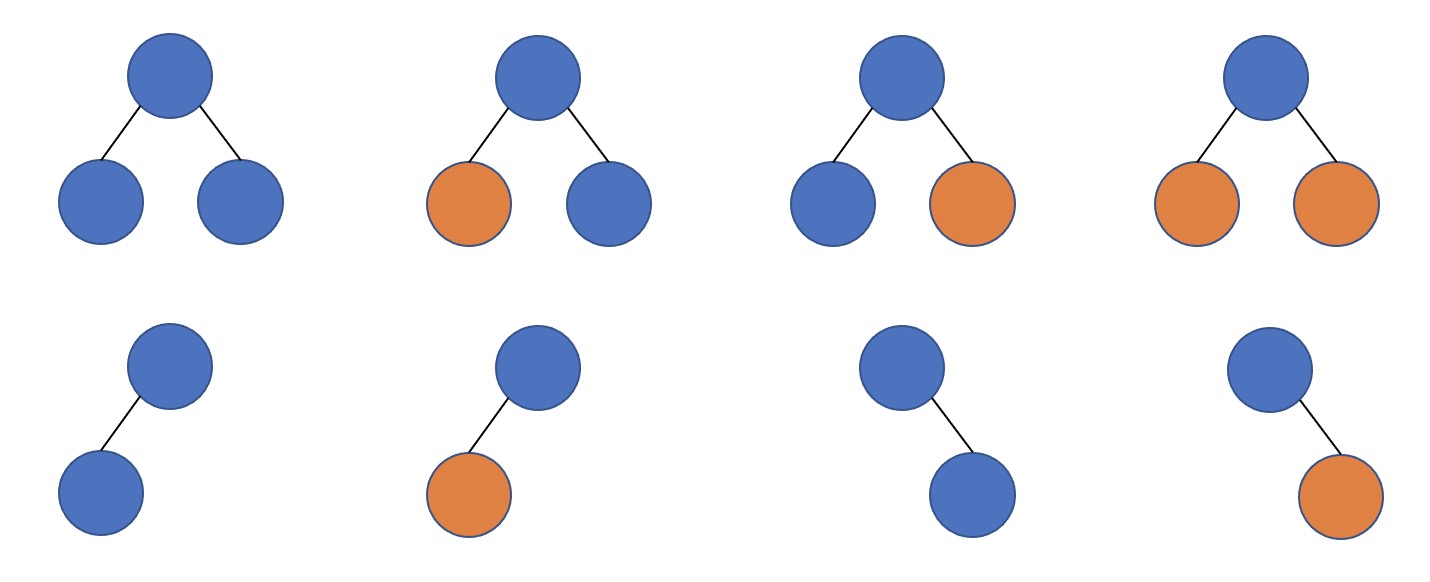
按照这样,我们重新合并图二中的树
但是接下来又要纠结了:带有特殊节点的合并是什么样的?我们不难遐想到有如下多种可能
合并的组合突然间多了很多。我们试图来讨论。但在讨论前,我们想要弄明白 特殊节点 的含义,就目前来看,它表示:除了特殊节点自身一个节点的树无法生成,其它任意子树皆可被生成。
首先,我们要排除上图中的 (1,4)(最右上角的),这种情况不具有意义。它表明:左右子树同时不能为自身。而在这样的限制条件下,无法产生的树的集合大小为 无限大(令左儿子为自身,右儿子形态任意),即使加强限制使得集合大小有限,该限制 不强于 其它七种情况,换句话说它是 没有用的。想避免此种情况,也就是说红色节点的个数必须 \(\le 1\)。
接着,我们来一一讨论。对于对称的情况我们可以转化,有用的情形总结如下:
\({\rm grow}(\)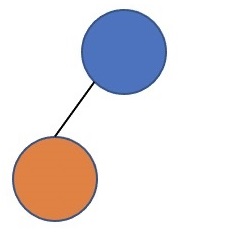 \()+{\rm grow}(\)
\()+{\rm grow}(\) \()+{\rm grow}(\)
\()+{\rm grow}(\) \()={\rm grow}(\)
\()={\rm grow}(\) \()\setminus\{\)
\()\setminus\{\) \(~+~\)
\(~+~\) \(\}\)
\(\}\)
\({\rm grow}(\) \()+{\rm grow}(\)
\()+{\rm grow}(\) \()+{\rm grow}(\)
\()+{\rm grow}(\) \()={\rm grow}(\)
\()={\rm grow}(\) \()\setminus\{\)
\()\setminus\{\) \(~+~\)
\(~+~\) \(~+~\)
\(~+~\)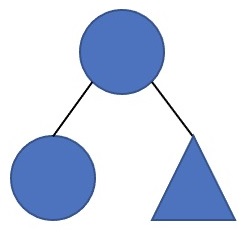 \(\}\)
\(\}\)
\({\rm grow}(\) \()+{\rm grow}(\)
\()+{\rm grow}(\) \()+{\rm grow}(\)
\()+{\rm grow}(\) \()={\rm grow}(\)
\()={\rm grow}(\) \()\setminus\{\)
\()\setminus\{\) \(~+~\)
\(~+~\) \(~+~\)
\(~+~\)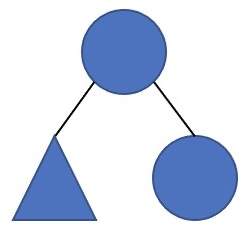 \(\}\)
\(\}\)
\({\rm grow}(\) \()+{\rm grow}(\)
\()+{\rm grow}(\)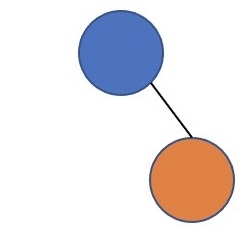 \()+{\rm grow}(\)
\()+{\rm grow}(\) \()={\rm grow}(\)
\()={\rm grow}(\) \()\setminus\{\)
\()\setminus\{\) \(~+~\)
\(~+~\) \(~+~\)
\(~+~\) \(\}\)
\(\}\)
\({\rm grow}(\) \()+{\rm grow}(\)
\()+{\rm grow}(\) \()+{\rm grow}(\)
\()+{\rm grow}(\) \()={\rm grow}(\)
\()={\rm grow}(\) \()\setminus\{\)
\()\setminus\{\) \(~+~\)
\(~+~\) \(~+~\)
\(~+~\) \(~+~\)
\(~+~\) \(\}\)
\(\}\)
三角形表示该点构成的子树形态任意。
发现第 2、3、5 种情况下,不可生成的部分中有一种情况,它可以拓展出无数种树。这也直接指出三棵树合并的错误之处了。这时发现第 5 组中:
\(\{\) \(\}+{\rm grow}(\)
\(\}+{\rm grow}(\) \()={\rm grow}(\)
\()={\rm grow}(\) \()\setminus\{\)
\()\setminus\{\) \(\}\)
\(\}\)
利用右边的红点,可以把右边的子树“封死”,而且不难证明该条件是必要的。这样不可生成的集合大小就是有限的了!
于是能推导出四棵树合并:
\({\rm grow}(\) \()+{\rm grow}(\)
\()+{\rm grow}(\) \()+{\rm grow}(\)
\()+{\rm grow}(\) \(\}+{\rm grow}(\)
\(\}+{\rm grow}(\) \()={\rm grow}(\)
\()={\rm grow}(\) \()\setminus\{\)
\()\setminus\{\) \(~+~\)
\(~+~\) \(~+~\)
\(~+~\) \(~+~\)
\(~+~\) \(\}\)
\(\}\)
可是右边的东西还是有点复杂?不过发现:等式右边都满足,由根生长的树,却不能在等式左边生长出来的数目是 有限的。如果拓宽 特殊点 的定义:特殊点所在的子树内对于数量 有限 的拓展下无法生成,除此之外其它基于原树拓展的部分均可生成。
不难发现上述合并法则依然成立!
为了统一,我们甚至可以
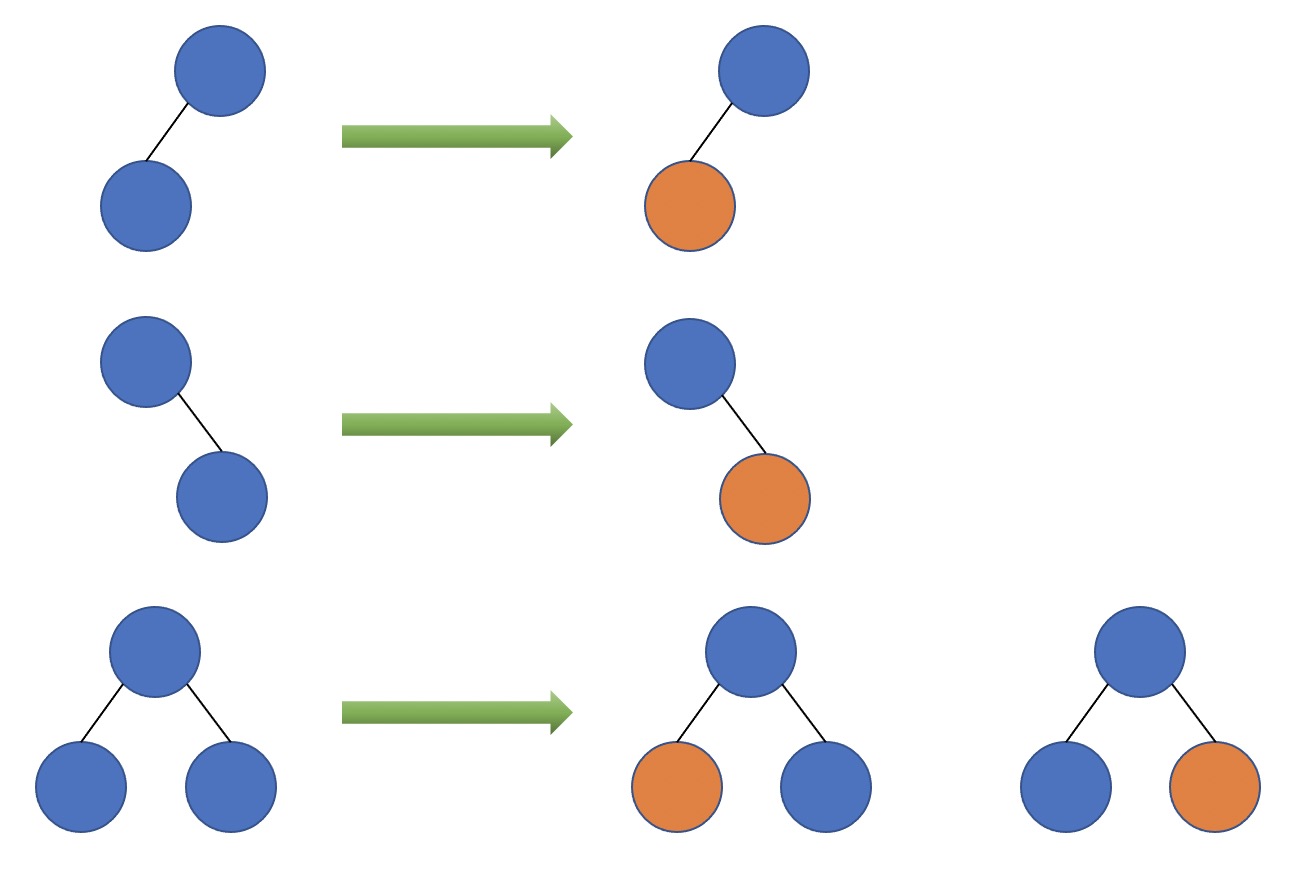
这样就可以将四棵树合并的策略适用于任何情况了。注意初始情况下 特殊节点 不可生成的树为空,但只要合并过,就一定非空,可以证明这样转换不会出现超出该合并法则的情况。
于是修正最开始三棵树合并的代码,使用 Hash 跑四棵树合并,即可通过本题。期望复杂度 \(\mathcal O(n)\)。
这道题还要用 Hash?Too weak!这里还有没挖掘的性质,可以大幅降低代码实现难度。
对于第二幅图中的树,它对答案是不起作用的,因为若干次合并后会出现这样的情况:

这与前面的推论矛盾了。什么样子的树在合并的过程中不会出现这样的情况?稍加思考可以发现,如果一个儿子合并了,另一个儿子不能合并。该种类树的形态:有一条主链,然后链上的每一个非叶子节点要么仅仅有一个节点,要么没有节点。
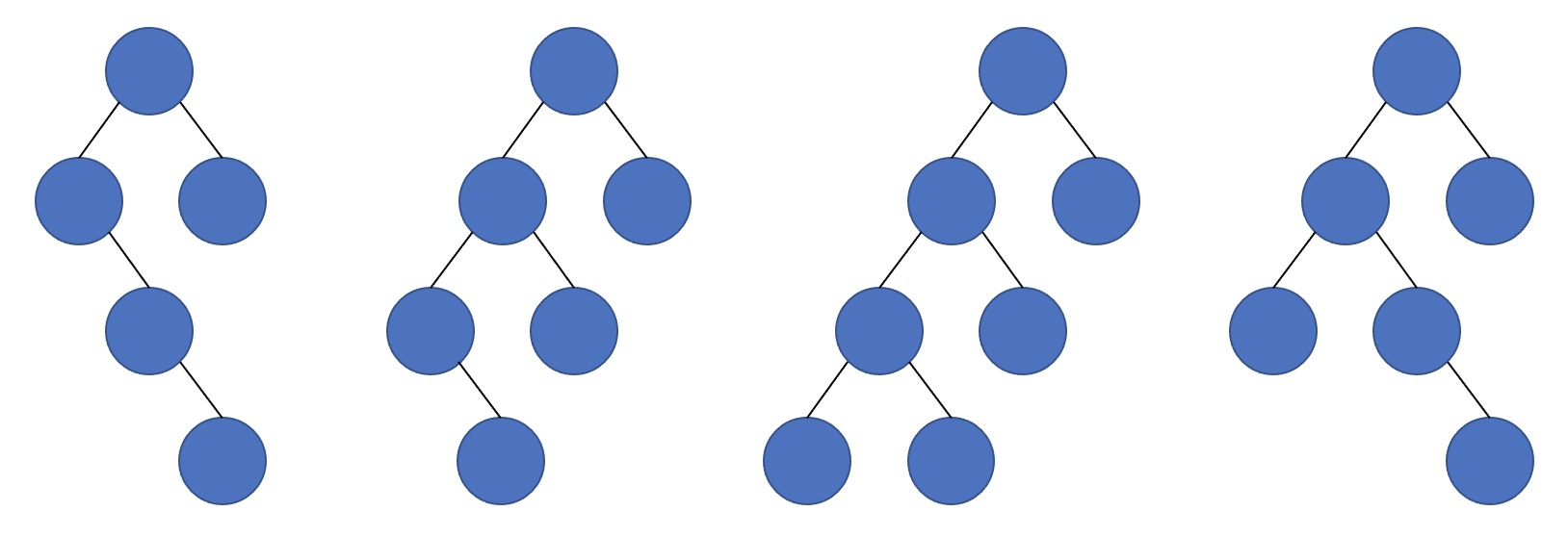
这跟官方题解中 树枝 的定义一致。官方题解中说:对于所有深度为 MAX_DEP 的树枝若均能被生成,则其 Almost Complete。而上面的合并,刚好符合这样的要求。
于是删掉无用的树之后,我们可以递归合并。这样就大幅简化代码了。复杂度仍然可以做到 \(\mathcal O(n)\)。
#include <bits/stdc++.h>
#define pb push_back
#define x first
#define y second
using std::vector; using std::pair;
const int N = 2e6 + 5;
int T, n, m;
vector<int> lc[N], rc[N];
vector<pair<int, int>> tmp;
int dfs(vector<pair<int, int>> A) {
vector<pair<int, int>> A0, A1, A2, A3;
if (!A.size()) return 0;
for (auto u : A) {
int x = lc[u.x][u.y], y = rc[u.x][u.y];
if (!x && !y) return 1;
if (!x || !y) x ? A0.pb({u.x, x}) : A1.pb({u.x, y});
else {
if (!lc[u.x][y] && !rc[u.x][y]) A2.pb({u.x, x});
if (!lc[u.x][x] && !rc[u.x][x]) A3.pb({u.x, y});
}
}
return dfs(A0) && dfs(A1) && dfs(A2) && dfs(A3);
}
void solve() {
scanf("%d", &n); tmp.clear();
for (int i = 1; i <= n; i++) {
scanf("%d", &m);
lc[i].resize(m + 1), rc[i].resize(m + 1);
for (int j = 1; j <= m; j++) scanf("%d%d", &lc[i][j], &rc[i][j]);
tmp.pb({i, 1});
}
puts(dfs(tmp) ? "Almost Complete" : "No");
}
int main() {
scanf("%d", &T);
while (T--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号